上海市宝山区2022年中考数学二模试题

试卷更新日期：2022-07-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各运算中，正确的运算是（　　　）

A、 $5 \sqrt{3} + 3 \sqrt{5} = 8 \sqrt{8}$ ； B、 $(- 3 a^{3})^{3} = - 27 a^{9}$ ； C、 $a^{8} \div a^{4} = a^{2}$ ； D、 $(a^{2} - b^{2})^{2} = a^{4} - b^{4}$ ．

查看试题解析
2. 若关于x的一元一次方程x−m+2=0的解是负数，则m的取值范围是（）

A、m≥2 B、m＞2 C、m＜2 D、m≤2

查看试题解析
3. 成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为（）

A、 $46 \times 10^{- 7}$ B、 $4.6 \times 10^{- 7}$ C、 $4.6 \times 10^{- 6}$ D、 $0.46 \times 10^{- 5}$

查看试题解析
4. 若数轴上表示-1和3的两点分别是点A和点B ，则点A和点B之间的距离是（）

A、-4 B、-2 C、2 D、4

查看试题解析
5. 如图，已知△ABC与△BDE都是等边三角形，点D在边AC上（不与点A、C重合），DE与AB相交于点F，那么与△BFD相似的三角形是（　　　）

A、△BFE； B、△BDC； C、△BDA； D、△AFD．

查看试题解析
6. 下列命题中正确的是 $()$

A、一组对边相等，另一组对边平行的四边形是等腰梯形 B、对角线互相垂直且相等的四边形是矩形 C、对角线互相平分且相等的四边形是正方形 D、对角线互相垂直平分的四边形是菱形

查看试题解析

二、填空题

7. 若 $a = b + 2$ ，则代数式 $a^{2} - 2 a b + b^{2}$ 的值为.

查看试题解析
8. 化简： $\frac{1}{a} - \frac{1}{3 a} =$ ．

查看试题解析
9. 如果一个数的平方等于5，那么这个数是．

查看试题解析
10. 方程 $\sqrt{x - 2} \cdot \sqrt{x - 1} = 0$ 的解是．

查看试题解析
11. 如果反比例函数 $y = \frac{k}{x} (k$ 是常数， $k \neq 0)$ 的图象经过点(-1，3)，那么当 $x > 0$ 时，y的值随x的值增大而.(填“增大”或“减小”)

查看试题解析
12. 《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等，交易其一，金轻十三两，问金、银一枚各重几何？”意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相同，两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计），问黄金、白银每枚各种多少两？设黄金重 $x$ 两，每枚白银重 $y$ 两，根据题意可列方程组为.

查看试题解析
13. 在一张边长为 4 的正方形纸上做扎针随机试验，纸上有一个半径为 1 的圆形阴影区域，则针头扎在阴影区域内的概率为．

查看试题解析
14. 董永社区在创建全国卫生城市的活动中，随机检查了本社区部分住户五月份某周内“垃圾分类”的实施情况，将他们绘制了两幅不完整的统计图（ $A$ .小于5天； $B$ .5天； $C$ .6天； $D$ .7天），则扇形统计图 $B$ 部分所对应的圆心角的度数是.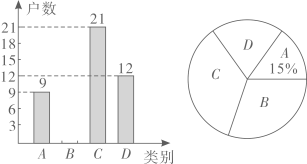

查看试题解析
15. 如图，点B、C、D在同一直线上，CE $∥$ AB， $∠ A C B = 90 °$ ，如果 $∠ E C D = 35 °$ ，那么 $∠ A =$ ．

查看试题解析
16. 如图，在ABC中，∠C＝90°，∠A＝30°，BD是∠ABC的平分线，如果 $\vec{A C} = \vec{x}$ ，那么 $\vec{C D}$ ＝（用 $\vec{x}$ 表示）．

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ B = 45 °$ ， $A C = 2$ ， $c o s C = \frac{3}{5} .$ $B C$ 的垂直平分线交 $A B$ 于点E，那么 $B E$ ： $A E$ 的值是．

查看试题解析
18. 如图1， $△ A B C$ 内有一点P，满足 $∠ P A B = ∠ C B P = ∠ A C P$ ，那么点P被称为 $△ A B C$ 的“布洛卡点”．如图2，在 $△ D E F$ 中， $D E = D F$ ， $∠ E D F = 90 °$ ，点P是 $△ D E F$ 的一个“布洛卡点”，那么 $t a n ∠ D F P =$ ．

查看试题解析

三、解答题

19. 计算： $(\sqrt{2})^{2} + (- \frac{π}{3})^{0} - 1 2^{\frac{1}{2}} + 2 （ t a n 60 ° - 1)^{- 1}$

查看试题解析
20. 解方程组： ${\begin{array}{l} x + y = 2 ① \\ x^{2} - x y - 6 y^{2} = 0 ② \end{array}$ ．

查看试题解析
21. 如图，在梯形 $A B C D$ 中， $A D$ ∥ $B C$ ， ∠ $B C D$ =90°， $A B = B C = 5$ ， $A D = 2 ，$

(1)、求 $C D$ 的长；

(2)、若∠ $A B C$ 的平分线交 $C D$ 于点E，连结 $A E$ ，求∠ $A E B$ 的正切值．

查看试题解析
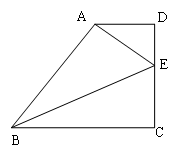22. 如图，是某型号新能源纯电动汽车充满电后，蓄电池剩余电量 $y$ （千瓦时）关于已行驶路程 $x$ （千米）的函数图象．

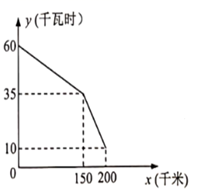(1)、根据函数图象，蓄电池剩余电量为35千瓦时汽车已经行驶的路程为千米．当 $0 \leq x \leq 150$ 时，消耗1千瓦时的电量，汽车能行驶的路程为千米．

(2)、当 $150 \leq x \leq 200$ 时，求 $y$ 关于 $x$ 的函数表达式，并计算当汽车已行驶160千米时，蓄电池的剩余电量．

查看试题解析
23. 已知：如图，在平行四边形ABCD中，AC、DB交于点E，点F在BC的延长线上，连结EF、DF，且∠DEF=∠ADC．

(1)、求证： $\frac{E F}{B F} = \frac{A B}{D B}$ ；

(2)、如果 $B D^{2} = 2 A D \cdot D F$ ，求证：平行四边形ABCD是矩形．

查看试题解析
24. 在平面直角坐标系 $x O y$ 中，抛物线 $y = \frac{1}{3} x^{2} + b x - 1$ 与x轴交于点A和点B(点A在x轴的正半轴上)，与y轴交于点C，已知 $t a n ∠ C A B = \frac{1}{3}$ ．

(1)、求顶点P和点B的坐标；

(2)、将抛物线向右平移2个单位，得到的新抛物线与y轴交于点M，求点M的坐标和 $△ A P M$ 的面积；

(3)、如果点N在原抛物线的对称轴上，当 $△ P M N$ 与 $△ A B C$ 相似时，求点N的坐标．

查看试题解析
25. 如图，在半径为3的圆O中， $O A$ 、 $O B$ 都是圆O的半径，且 $∠ A O B = 90 °$ ，点C是劣弧 $\overset{⌢}{A B}$ 上的一个动点(点C不与点A、B重合)，延长 $A C$ 交射线 $O B$ 于点D．

(1)、当点C为线段 $A D$ 中点时，求 $∠ A D B$ 的大小；

(2)、如果设 $A C = x$ ， $B D = y$ ，求y关于x的函数解析式，并写出定义域；

(3)、当 $A C = \frac{18}{5}$ 时，点E在线段 $O D$ 上，且 $O E = 1$ ，点F是射线 $O A$ 上一点，射线 $E F$ 与射线 $D A$ 交于点G，如果以点A、G、F为顶点的三角形与 $△ D G E$ 相似，求 $\frac{S_{△ A G F}}{S_{△ D G E}}$ 的值．

查看试题解析