辽宁省沈阳市铁西区2022年九年级中考一模数学试卷

试卷更新日期：2022-07-06 类型：中考模拟

进入出卷网下载

一、单选题

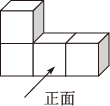
1. 在实数 $- \sqrt{2}$ ， $\frac{1}{2}$ ， 0，－2中，最大的数是（）

A、 $- \sqrt{2}$ B、 $\frac{1}{2}$ C、0 D、－2

查看试题解析
2. 如图是由四个完全相同的正方体组成的几何体，其左视图是（）

A、 B、 C、 D、

查看试题解析
3. 第24届冬奥会于2022年2月4日至2月20日在中国北京和张家口成功举办，本届冬奥会的运动员达到2892人，历史规模第二．数据2892用科学记数法表示应是（）

A、 $0.2892 \times 1 0^{4}$ B、 $2.892 \times 1 0^{4}$ C、 $2.892 \times 1 0^{3}$ D、 $28.92 \times 1 0^{3}$

查看试题解析
4. 计算 $2 a^{3} \cdot 5 a^{3}$ 的结果是（）

A、 $10 a^{6}$ B、 $10 a^{9}$ C、 $7 a^{3}$ D、 $7 a^{6}$

查看试题解析
5. 如图，在 $△ A B C$ 中， $∠ B = 50 °$ ， $∠ C = 70 °$ ，直线 $D E$ 经过点A ， $∠ D A B = 50 °$ ，则 $∠ E A C$ 的度数是（）

A、40° B、50° C、60° D、70°

查看试题解析
6. 一次函数y＝kx﹣2（k≠0）的函数值y随x增大而减小，那么该函数的图象不经过（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 在学校举行的团体操比赛中，七位评委给某班的评分去掉一个最高分、一个最低分后得到五个有效评分，分别为：9.20，9.20，9.40，8.80，9.00（单位：分），这五个有效评分的平均数是（）

A、9.20 B、9.12 C、9.10 D、9.08

查看试题解析
8. 如图，在 $△ A B C$ 中，点D，E分别在边AB，AC上， $D E ∥ B C$ ， $E F ∥ C D$ 交边AB于点F，那么下列比例式中正确的是（）

A、 $\frac{A F}{D F} = \frac{D E}{B C}$ B、 $\frac{D F}{D B} = \frac{A F}{D F}$ C、 $\frac{A F}{A D} = \frac{A D}{A B}$ D、 $\frac{A F}{B D} = \frac{A E}{E C}$

查看试题解析
9. 下列说法正确的是（）

A、为了了解某电视剧的收视率，选择全面调查 B、在一组数据7，3，5，6，6，4，2中，众数和中位数相同 C、“若a是实数，则 $a^{2} > 0$ ”是必然事件 D、若甲组数据的方差 ${S_{甲}}^{2} = 12$ ，乙组数据的方差 ${S_{乙}}^{2} = 8$ ，则乙组数据比甲组数据稳定

查看试题解析
10. 如图，AB是 $⊙ O$ 的切线，切点为点A，连接OB交 $⊙ O$ 于点C，过点A作 $A D ∥ O B$ 交 $⊙ O$ 于点D，连接CD，若 $∠ B = 32 °$ ，则 $∠ O C D$ 的度数为（）

A、32° B、29° C、28° D、26°

查看试题解析

二、填空题

11. 分解因式： $2 m^{3} - 32 m =$ ．

查看试题解析
12. 一个不透明的袋子里装有4个红球和2个黄球，它们除颜色外其余都相同．从袋中任意摸出一个球是红球的概率为．

查看试题解析
13. 在一元一次不等式组 ${\begin{array}{l} 2 x + 1 > 0 \\ x - 5 \leq 0 \end{array}$ 的解集中，整数解有个．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A B = A C$ ， AB的垂直平分线交AB于点D，交AC于点E．已知 $△ B C E$ 的周长为8， $A C - B C = 2$ ，则AC的长为．

查看试题解析
15. 在同一平面直角坐标系中，一次函数y₁＝k₁x+b与反比例函数y₂ $= \frac{k_{2}}{x}$ （x＞0）的图象如图所示．则当y₁＞y₂时，自变量x的取值范围为．

查看试题解析
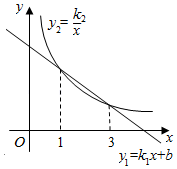16. 如图，在平面直角坐标系中，点A的坐标为 $(0 ， 6)$ ，点B的坐标为 $(- 6 ， 0)$ ，点C是线段AO上的一个动点，连接BC， $O D ⊥ B C$ 于点D，以OD为一边，作正方形ODEF，其中点E与点B在直线OD两侧，当点C从点A运动到点O过程中，点E经过的路径长为．

查看试题解析

三、解答题

17. 计算： ${(- 2022)}^{0} + {(\frac{1}{2})}^{- 1} - (- 4) + 2 \sqrt{3} t a n 60 °$ ．

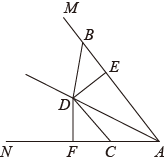
查看试题解析
18. 如图，点B，C在 $∠ M A N$ 的边AM，AN上，点D在 $∠ M A N$ 内部，连接BD，CD， $B D = C D$ ，作 $D E ⊥ A M$ 于点E， $D F ⊥ A N$ 于点F， $B E = C F$ ，求证：AD是 $∠ M A N$ 的平分线．

查看试题解析
19. 有两把不同的锁（记为A，B），四把不同的钥匙（记为a，b，c，d），其中钥匙a只能打开锁A，钥匙b只能打开锁B，钥匙c和d都不能打开这两把锁．现在任意取出一把钥匙去开任意一把锁，请用树状图法或列表法求一次就能打开锁的概率．

查看试题解析
20. 某校为了解线上教学九年级学生的学习效果，抽取了部分学生进行了一次综合测试，并将测试结果分成四个类别：A：优秀；B：良好；C：合格；D：待合格．并将调查结果绘制成如下两幅不完整的统计图．
请根据统计图解答下列问题：

(1)、本次调查中，一共调查了名学生；

(2)、在各类别学生人数扇形统计图中，D类别所在扇形的圆心角是度；

(3)、补全条形统计图；

(4)、若该校九年级共有760名学生，请估计此次综合测试C类别的学生有多少名．

查看试题解析
21. 某航空公司为了保证C检工作正常进行，事先组织机务人员到外地跟班学习C检工作，后又具体分析研究，周密地制订出C检的具体实施方案，因而工作效率提高了30%，经过31名机务人员的艰苦努力，终于提前6天完成了C检，为公司节约了数十万元的维修费用．请问：原计划多少天完成C检？（根据飞机维护规定，一架飞机每飞行250h，要进行一次定期检查，称为A检；每飞行3000h，就要进行一次中大修性质的全面维护、保养、检查工作，称为C检．）

查看试题解析
22. 如图，A，B，C，D是 $⊙ O$ 上的四个点， $A B = A C$ ， AD交BC于点E， $A E = 2$ ， $E D = 4$ ，

(1)、求AB的长；

(2)、若 $∠ A D B = 30 °$ ，连接OA，OC，则扇形OAC的面积为．（结果保留 $π$ ）

查看试题解析
23. 如图，直线 $y = - \frac{1}{3} x + 2$ 与x轴交于点A，与y轴交于点B．

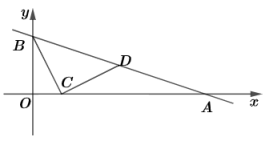(1)、求点A和点B的坐标；

(2)、点C是x轴上一点，点D是线段AB的中点，当 $B C + C D$ 最短时，求点C的坐标；

(3)、在（2）的条件下，点M是坐标轴上一点，且 $△ A D M$ 是以AD为直角边的直角三角形，请直接写出点M的坐标．

查看试题解析
24.

(1)、如图1，正方形ABCD中，点E在AB边上， $B E = 5$ ，连接CE，将 $△ B C E$ 沿直线CE折叠，得到 $△ F C E$ ，点F落在正方形ABCD内部，连接BF并延长交边AD于点G，延长CF交边AD于点H．
①求证： $B G = C E$ ；
②若 $H G ： A H = 2 ： 3$ ，则边CD的长为_▲_；

(2)、如图2，矩形ABCD中， $A B ： B C = 4 ： 5$ ，点E在AB边上， $B E = 5$ ，连接CE．将 $△ B C E$ 沿直线CE折叠，得到 $△ F C E$ ，点F落在矩形ABCD内部，连接BF并延长交边AD于点G，延长CF交边AD于点H，若 $H G ： A H = 2 ： 3$ ，请直接写出边CD的长．

查看试题解析
25. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + \frac{3}{2} x + c$ 与x轴交于点A，B，与y轴交于点C，点A和点C的坐标分别为 $(- 1 ， 0)$ 和 $(0 ， 2)$

(1)、求抛物线 $y = a x^{2} + \frac{3}{2} x + c$ 的函数表达式；

(2)、将线段CB绕点C顺时针旋转90°，得到线段CD，连接AD，求线段AD的长；

(3)、点M是抛物线上位于第一象限图象上的一动点，连接AM交BC于点N，连接BM，当 $S_{△ B M N} = \frac{1}{4} S_{△ A B N}$ 时，请直接写出点M的横坐标的值．

查看试题解析