辽宁省沈阳市沈河区2022年九年级中考模拟（一模）数学试题

试卷更新日期：2022-07-06 类型：中考模拟

进入出卷网下载

一、单选题

1. -2022的倒数是（）

A、2022 B、 $- 2022$ C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 根据国家统计局数据显示，我国冰雪运动参与人数达到346000000人.数据346000000用科学记数法表示为（）

A、 $0.346 \times 1 0^{9}$ B、 $3.46 \times 1 0^{8}$ C、 $346 \times 1 0^{6}$ D、 $3.46 \times 1 0^{9}$

查看试题解析
3. 如图，该几何体是由6个大小相同的小正方体堆成的，则该几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 化简 $(1 + \frac{1}{a - 1}) \div \frac{a}{a - 1}$ 的结果是（　　）

A、1 B、 $\frac{a + 1}{a}$ C、 $\frac{a - 1}{a}$ D、 $\frac{a + 1}{a}$

查看试题解析
5. 在平面直角坐标系中，已知点 $(2 ， m)$ ， $(- 1 ， n)$ 都在直线 $y = 3 x + b$ 上，则m，n的大小关系是（）

A、 $m > n$ B、 $m = n$ C、 $m < n$ D、不能确定

查看试题解析
6. 如图，AB、BC为 $⊙ O$ 的两条弦，连接OA、OC，点D为AB的延长线上一点，若 $∠ C B D = 62 °$ ，则 $∠ A O C$ 的度数为（）

A、100° B、118° C、124° D、130°

查看试题解析
7. 为了了解学生学科作业量，某中学对学生做周末学科作业的时间进行抽样调查，结果如下表：
时间（小时）
1
2
3
4
学生人数（人）
3
12
9
6
关于“周末做学科作业时间”这组数据说法正确的是（）

A、中位数是2.5 B、中位数是2 C、众数是4 D、众数是12

查看试题解析
8. 已知x，y满足方程组 ${\begin{array}{l} x + 5 y = 6 \\ 3 x - y = 2 \end{array}$ ，则 $x + y$ 的值为（）

A、-2 B、-3 C、2 D、3

查看试题解析
9. 如图，小明在点C处测得树的顶端A仰角为α，同时测得AC＝15m，则树的高度AB为（　　）m．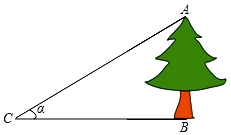

A、15sinα B、 $\frac{15}{s i n a}$ C、15tanα D、 $\frac{15}{t a n a}$

查看试题解析

10. 二次函数

y = a x^{2} + b x + c

（a，b，c是常数，

a \neq 0

）的自变量x与函数值y的部分对应值如下表：

$x$	…	-2	-1	0	1	2	…
$y = a x^{2} + b x + c$	…	$t$	$m$	-2	-2	$n$	…

且当 $x = - \frac{1}{2}$ 时，与其对应的函数值 $y > 0$ ，有下列结论：① $a b c < 0$ ；②图象的顶点在第三象限；③m=n；④-2和3是关于x的方程 $a x^{2} + b x + c = t$ 的两个根．其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 分解因式： $a^{3} - 9 a =$ ．

查看试题解析
12. 在一个不透明的盒子中装有红球和白球共20个，这些球除颜色外无其它差别，随机从盒子中摸出一个球，记下球的颜色后，放回并摇匀．通过大量的实验后发现摸出白球的频率稳定在0.4，则盒子中白球大约有个．

查看试题解析
13. 不等式组 ${\begin{array}{l} 2 x - 1 < 1 \\ \frac{1}{2} (x + 13) > 3 \end{array}$ 的解集为．

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，分别以点A和B为圆心，以大于 $\frac{1}{2} A B$ 的长为半径作弧，两弧相交于点M和N，作直线MN交AB于点D，交BC于点E，连接CD，若 $∠ B = 2 ∠ C D E$ ，则 $∠ B$ 的度数为．

查看试题解析
15. 某商场进货员预测一种应季衬衫能畅销市场，就用8万元购进这种衬衫，面市后果然供不应求，商场又用17.2万元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了4元，很快售完，商场第二批销售这种衬衫件．

查看试题解析
16. 当一个凸四边形的一条对角线把原四边形分割成两个等腰三角形时，我们称这个四边形为“双等腰四边形”，其中这条对角线叫做这个四边形的“等腰线”．如果凸四边形ABCD是“双等腰四边形”，对角线BD是该四边形的“等腰线”，其中 $∠ A B C = 90 °$ ， $A B = B C = C D = 6 \neq A D$ ，那么凸四边形ABCD的面积为．

查看试题解析

三、解答题

17. 计算： $2 s i n 60 ° - {(π + 2022)}^{0} + | 2 - \sqrt{3} | + {(- \frac{1}{3})}^{2}$ ．

查看试题解析
18. 冰墩墩将熊猫形象与富有超能量的冰晶外壳相结合，整体形象酷似航天员，凭借憨态可掬的模样和活泼调皮的性格，成为新晋“顶流”，同时形成了“一墩难求”的局面，小丽爸爸买了四个外包装完全相同的冰墩墩手办，其中两个为经典造型（用 $A_{1}$ ， $A_{2}$ 表示），两个为冰球造型（用 $B_{1}$ ， $B_{2}$ 表示），在没有拆外包装的情况下，小丽和哥哥各自从这四个手办中随机拿走一个．

(1)、若小丽从这四个手办中拿走一个，则小丽拿走的是经典造型的概率为；

(2)、若小丽先拿走一个，哥哥再从剩下的三个中随机拿走一个，利用列表或画树状图法求小丽和哥哥拿走的手办是相同造型的概率．

查看试题解析
19. 如图，在平行四边形ABCD中，对角线AC，BD相交于点 $O$ ， $A C ⊥ C D$ ，点E是BC的中点，过点E作 $E F ∥ A C$ ，交AB于点F．

(1)、求证：四边形AOEF是矩形；

(2)、若 $C D = 16$ ，矩形AOEF的面积为120，请直接写出 $c o s ∠ A B C$ 的值．

查看试题解析
20. 为了解家长们对“双减政管”的了解情况，从某校1600名家长中随机抽取部分家长进行问卷调查，调查评价结果分为“了解较少”“基本了解”“了解较多”“非常了解”四类，并根据调查结果绘制出如图所示的两幅不完整的统计图.

(1)、本次抽取家长共有人；其中“基本了解”的占%；

(2)、直接补全条形统计图；

(3)、估计此校“非常了解”和“了解较多”的家长一共有多少人?

查看试题解析
21. 如图，在平面直角坐标系中，直线 $y = \frac{1}{2} x + b$ 与x轴交于点 $A (4 ， 0)$ ，与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交于点 $B (6 ， m)$ ， $D (0 ， n)$ 是y轴正半轴上的一个动点，且四边形 $A B C D$ 是平行四边形．

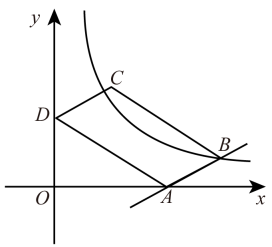(1)、求k和m的值；

(2)、若点C落在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上，则边 $B C$ 的长为；

(3)、当 $A C$ 的中点落在反比例函数的图象上时， $▱ A B C D$ 的面积是．

查看试题解析
22. 如图，AB是 $⊙ O$ 的直径，点C，D在 $⊙ O$ 上，且AD平分 $∠ C A B$ ，过点D作AC的垂线，与AC的延长线相交于点E，与AB的延长线相交于点F．

(1)、求证：EF与 $⊙ O$ 相切；

(2)、若 $A B = 10$ ， $A D = 3 \sqrt{10}$ ，则 $t a n ∠ D A F$ 的值为．

查看试题解析
23. 如图，在平面直角坐标系中，一次函数 $y = \frac{3}{4} x + 12$ 的图象分别交x，y轴于点A和B，与经过点 $C (\frac{3}{2} ， 0)$ ， $D (0 ， - 3)$ 的直线交于点E．

(1)、求直线CD的函数解析式及点E的坐标；

(2)、点P是线段DE上的动点，连接BP．
①当BP分 $△ B D E$ 面积为1：2时，请直接写出点P的坐标；

②将 $△ B P E$ 沿着直线BP折叠，点E对应点 $E^{'}$ ，当点 $E^{'}$ 落在坐标轴上时，直接写出点P的坐标．

查看试题解析
24. 在 $△ A B C$ 中， $A B = A C = 5$ ， $B C = 6$ ，将 $△ A B C$ 绕点A顺时针旋转 $α ° (0 < α < 180)$ 得到 $△ A B^{'} C^{'}$ ，射线 $B^{^{'}} C^{^{'}}$ 交直线BC于点D，过点A作射线 $A E ∥ B^{'} C^{'}$ ，交直线BC于点E．

(1)、如图1，当点E是BC的中点时，AE的长为， $\frac{C E}{A E}$ 的值为；

(2)、如图2，当点E与B重合时，求证：四边形 $A B D C^{'}$ 是菱形；

(3)、当点C，D，E中有一个点是其它两点构成线段的中点时，请直接写出线段DE的长．

查看试题解析
25. 在平面直角坐标系中，抛物线 $y = a x^{2} + b x + 4 (a \neq 0)$ 与x轴交于点 $A (- 4 ， 0)$ 和 $B (1 ， 0)$ ，交y轴于点C，点P是抛物线上的一个动点．

(1)、求抛物线的解析式；

(2)、如图1，当点P在AC上方时，作 $P D ∥ y$ 轴，交AC于点D，过PD中点E作 $E F ∥ x$ 轴，交直线AC于点F，作 $F G ⊥ O A$ 于点G，当 $P D = F G$ 时，求线段 $F G$ 的长；

(3)、如图2，取AC中点I，点M，N是射线OI上的两个动点（点M在N的左侧），且 $M N = 2 \sqrt{2}$ ，将点M向上平移2个单位长度至点 $J$ ，点H是x轴正半轴上的一点，且 $O H = \frac{\sqrt{2}}{2} O M$ ，连接MH和NJ交于点K，请直接写出点K的运动路径与抛物线交点P的横坐标．

查看试题解析

时间（小时）	1	2	3	4
学生人数（人）	3	12	9	6