辽宁省沈阳市沈北新区2022年中考一模考试数学试题
试卷更新日期:2022-07-06 类型:中考模拟
一、单选题
-
1. 四个数: , 0, , 中最大的数是( )A、 B、0 C、 D、2. 用科学记数法表示0.000031,结果正确的是( )A、 B、 C、 D、3. 已知反比例函数的图象经过点(2,﹣4),那么这个反比例函数的解析式是( )A、y= B、y=﹣ C、y= D、y=﹣4. 不等式 的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、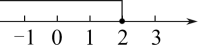 D、
D、 5. 下列各式中,计算正确的是( )A、 B、 C、 D、6. 如图, , 分别与 , 交于点 , .若 , ,则 的度数是( )
5. 下列各式中,计算正确的是( )A、 B、 C、 D、6. 如图, , 分别与 , 交于点 , .若 , ,则 的度数是( ) A、 B、 C、 D、7. 直线()与直线()的交点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 某班在体育活动中,测试了十位学生的“一分钟跳绳”成绩,得到十个各不相同的数据.在统计时,出现了一处不符合题意:将最高成绩写得更高了,则计算结果不受影响的是( )A、平均数 B、中位数 C、方差 D、众数9. 如图, , , 是 上的三个点, , ,则 的度数是( )
A、 B、 C、 D、7. 直线()与直线()的交点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 某班在体育活动中,测试了十位学生的“一分钟跳绳”成绩,得到十个各不相同的数据.在统计时,出现了一处不符合题意:将最高成绩写得更高了,则计算结果不受影响的是( )A、平均数 B、中位数 C、方差 D、众数9. 如图, , , 是 上的三个点, , ,则 的度数是( ) A、 B、 C、 D、10. 已知二次函数的图象如图所示,有以下4个结论:①;②;③;④ , 其中正确的结论有( )
A、 B、 C、 D、10. 已知二次函数的图象如图所示,有以下4个结论:①;②;③;④ , 其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 分解因式: .12. 将二次函数转化成顶点式为: .13. 如图,在平面直角坐标系中,O是坐标原点,中,点A在反比例函数的图象上,点B在x轴上, , 于点C,若 , 则k的值为 .
 14. 如图,一条东西向的大道上,A,B两景点相距 , C景点位于A景点北偏东方向上,位于B景点北偏北西方向上,则A,C两景点相距 .
14. 如图,一条东西向的大道上,A,B两景点相距 , C景点位于A景点北偏东方向上,位于B景点北偏北西方向上,则A,C两景点相距 .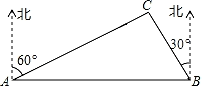 15. 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是 .
15. 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是 . 16. 如图,在△ABC中∠C=90°,AC=6,BC=8.点D是BC上的中点.点P是边AB上的动点,若要使△BPD为直角三角形,则BP= .
16. 如图,在△ABC中∠C=90°,AC=6,BC=8.点D是BC上的中点.点P是边AB上的动点,若要使△BPD为直角三角形,则BP= .
三、解答题
-
17. 先化简,再求值:
, 请在﹣3,0,1,3中选择一个适当的数作为x值.
18. 为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表:学生每月零花线频数分布表:
零花钱数额x/元
人数(频数)
频率
6
0.15
12
0.30
16
0.40
b
0.10
2
a
学生每月零花钱频数直方图:
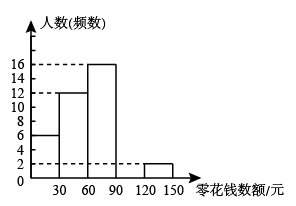
请根据以上图表,解答下列问题:
(1)、这次被调查的人数共有人, , ;(2)、计算并补全频数分布直方图;(3)、请估计该校1500名学生中每月零花钱数额低于90元的人数.19. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到A小区的概率是多少(2)、请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.20. 如图,在四边形ABCD中,AD∥BC , BA=BC , BD平分∠ABC . (1)、求证:四边形ABCD是菱形;(2)、过点D作DE⊥BD , 交BC的延长线于点E , 若BC=5,BD=8,求四边形ABED的周长.21. 某口罩生产厂生产的口罩1月份平均日产量为20000,1月底因突然爆发新冠肺炎疫情,市场对口罩需求量大增,为满足市场需求,工厂决定从2月份起扩大产能,3月份平均日产量达到24200个.(1)、求口罩日产量的月平均增长率;(2)、按照这个增长率,预计4月份平均日产量为多少?22. 如图,是的外接圆,是的直径, .
(1)、求证:四边形ABCD是菱形;(2)、过点D作DE⊥BD , 交BC的延长线于点E , 若BC=5,BD=8,求四边形ABED的周长.21. 某口罩生产厂生产的口罩1月份平均日产量为20000,1月底因突然爆发新冠肺炎疫情,市场对口罩需求量大增,为满足市场需求,工厂决定从2月份起扩大产能,3月份平均日产量达到24200个.(1)、求口罩日产量的月平均增长率;(2)、按照这个增长率,预计4月份平均日产量为多少?22. 如图,是的外接圆,是的直径, . (1)、求证:是的切线;(2)、若 , 垂足为交于点F;求证:是等腰三角形.23. 如图,已知点A在x轴的负半轴上,点B在y轴的正半轴上, , , 点P在线段上,从点A出发以每秒5个单位长度的速度向点B运动,设运动时间为秒,过点P作轴于点Q.
(1)、求证:是的切线;(2)、若 , 垂足为交于点F;求证:是等腰三角形.23. 如图,已知点A在x轴的负半轴上,点B在y轴的正半轴上, , , 点P在线段上,从点A出发以每秒5个单位长度的速度向点B运动,设运动时间为秒,过点P作轴于点Q. (1)、当时,线段的长为;(2)、当时,求t的值;(3)、在x轴上是否存在点M,使为等腰三角形,若存在,直接写出点M的坐标,若不存在,说明理由.
(1)、当时,线段的长为;(2)、当时,求t的值;(3)、在x轴上是否存在点M,使为等腰三角形,若存在,直接写出点M的坐标,若不存在,说明理由.

