辽宁省沈阳市浑南区2022年九年级中考一模数学试卷
试卷更新日期:2022-07-06 类型:中考模拟
一、单选题
-
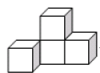
1. -3的相反数是( )A、 B、-3 C、3 D、2. 右图是由四个小正方体叠成的一个立体图形,那么它的俯视图是( )
 A、
A、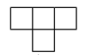 B、
B、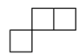 C、
C、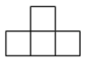 D、
D、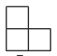 3. 2021年5月11日,第七次全国人口普查数据显示,全国人口比第六次全国人口普查数据增加了7206万人.将数据7206万用科学记数法表示( )A、 B、 C、 D、4. 下列计算中,正确的是( )A、 B、 C、 D、5. 如图,在 中, , 平分 ,则 的度数为( )
3. 2021年5月11日,第七次全国人口普查数据显示,全国人口比第六次全国人口普查数据增加了7206万人.将数据7206万用科学记数法表示( )A、 B、 C、 D、4. 下列计算中,正确的是( )A、 B、 C、 D、5. 如图,在 中, , 平分 ,则 的度数为( ) A、 B、 C、 D、6. 在平面直角坐标系中,若将一次函数的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )A、-5 B、5 C、-6 D、67. 下列说法正确的是( )A、掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件 B、甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 C、“明天降雨的概率为”,表示明天有半天都在降雨 D、了解一批电视机的使用寿命,适合用普查的方式8. 有19位同学参加歌咏比赛,所得的分数互不相同,取得分前10位的同学进入决赛,某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学分数的( )A、平均数 B、中位数 C、众数 D、方差9. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为 , 则a与b的数量关系为( )
A、 B、 C、 D、6. 在平面直角坐标系中,若将一次函数的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )A、-5 B、5 C、-6 D、67. 下列说法正确的是( )A、掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件 B、甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 C、“明天降雨的概率为”,表示明天有半天都在降雨 D、了解一批电视机的使用寿命,适合用普查的方式8. 有19位同学参加歌咏比赛,所得的分数互不相同,取得分前10位的同学进入决赛,某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学分数的( )A、平均数 B、中位数 C、众数 D、方差9. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为 , 则a与b的数量关系为( ) A、 B、 C、 D、10. 如图,点 在 上, ,则 ( )
A、 B、 C、 D、10. 如图,点 在 上, ,则 ( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
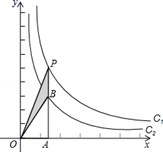
11. 因式分解 = .12. 不等式组 的解集是.13. 化简的结果是 .14. 如图,两个反比例函数 和 在第一象限内的图象分别是C1和C2 , 设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为 .
 15. 某高档游泳健身馆每人每次游泳健身的票价为80元,每日平均客流量为136人,为了促进全民健身运动,游泳馆决定降价促销,经市场调查发现,票价每下降1元,每日游泳健身的人数平均增加2人.当每日销售收入最大时,票价下调元.16. 在平面直角坐标系中,A点坐标为 , 直线交x轴于点B,交y轴于点C,第一象限内有一动点P,且满足 , 则周长的最小值为 .
15. 某高档游泳健身馆每人每次游泳健身的票价为80元,每日平均客流量为136人,为了促进全民健身运动,游泳馆决定降价促销,经市场调查发现,票价每下降1元,每日游泳健身的人数平均增加2人.当每日销售收入最大时,票价下调元.16. 在平面直角坐标系中,A点坐标为 , 直线交x轴于点B,交y轴于点C,第一象限内有一动点P,且满足 , 则周长的最小值为 .三、解答题
-
17. 计算: .18. 在一个不透明的袋子中装有白色、黄色和蓝色三种颜色的小球,这些球除颜色外都相同,其中白球有2个,蓝球有1个.现从中任意摸出一个小球是白球的概率是 .(1)、袋子中黄色小球有个;(2)、如果第一次任意摸出一个小球(不放回),第二次再摸出一个小球,请用画树状图或列表格的方法求两次都摸出白球的概率.19.
如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.
 (1)、若DE=BF,求证:四边形AFCE是平行四边形;(2)、若四边形AFCE是菱形,求菱形AFCE的周长.20. 初中生对待学习的态度一直是教育工作者关注的问题之一.为此某市教育局对该市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)、若DE=BF,求证:四边形AFCE是平行四边形;(2)、若四边形AFCE是菱形,求菱形AFCE的周长.20. 初中生对待学习的态度一直是教育工作者关注的问题之一.为此某市教育局对该市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题: (1)、此次抽样调查中,共调查了名学生;(2)、将图①补充完整;(3)、求出图②中C级所占的圆心角的度数;(4)、根据抽样调查结果,请你估计该市近20000名初中生中大约有多少名学生学习态度达标(达标包括A级和B级)?21. 甲乙两人制作某种机械零件.已知甲每小时比乙多做3个,甲做96个所用时间与乙做84个所用时间相等,求甲乙两人每小时各做多少个零件?22.
(1)、此次抽样调查中,共调查了名学生;(2)、将图①补充完整;(3)、求出图②中C级所占的圆心角的度数;(4)、根据抽样调查结果,请你估计该市近20000名初中生中大约有多少名学生学习态度达标(达标包括A级和B级)?21. 甲乙两人制作某种机械零件.已知甲每小时比乙多做3个,甲做96个所用时间与乙做84个所用时间相等,求甲乙两人每小时各做多少个零件?22.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
 (1)、求证:∠BDC=∠A;(2)、若CE=4,DE=2,求AD的长.23. 如图,在平面直角坐标系中,点A的坐标为 , 点B的坐标为 , 直线经过点A和点B,直线与x轴交于点C,与y轴交于点D,直线与直线相交于点P.
(1)、求证:∠BDC=∠A;(2)、若CE=4,DE=2,求AD的长.23. 如图,在平面直角坐标系中,点A的坐标为 , 点B的坐标为 , 直线经过点A和点B,直线与x轴交于点C,与y轴交于点D,直线与直线相交于点P. (1)、求直线的表达式和点P的坐标;(2)、正方形EFGH的边EF与线段AO重合,点G在x轴的正半轴上,将正方形EFGH沿射线AB的方向平移,边EH始终与x轴平行.已知正方形EFGH以每秒5个单位的速度匀速移动(点E移动到点B时停止移动),设移动时间为t秒;
(1)、求直线的表达式和点P的坐标;(2)、正方形EFGH的边EF与线段AO重合,点G在x轴的正半轴上,将正方形EFGH沿射线AB的方向平移,边EH始终与x轴平行.已知正方形EFGH以每秒5个单位的速度匀速移动(点E移动到点B时停止移动),设移动时间为t秒;①正方形EFGH在移动过程中,当点F落在直线上时,请求出此时t的值;
②正方形EFGH在移动过程中,设正方形EFGH与重合部分的面积为S,当时,请直接写出此时t的值.
24. 如图1,在中, , 于点O, , , 在的外部以AB为边作等边 , 点E是线段AO所在直线上一动点(点E不与点A重合),将线段BE绕点B顺时针方向旋转60°得到线段BF,连接EF.

 (1)、求AO的长;(2)、如图2,当点E在线段AO上,且点F,E,C三点在同一条直线上时,求BF的长;(3)、连接DF,若的面积为3,请直接写出BF的长.25. 如图,抛物线与x轴相交于点 , , 与y轴相交于点 , 抛物线的对称轴与x轴相交于点D,点E是x轴下方抛物线上的一个动点(点E,D,C不在同一条直线上),分别过点A,B作直线CE的垂线,垂足分别为M,N,连接MD,ND.
(1)、求AO的长;(2)、如图2,当点E在线段AO上,且点F,E,C三点在同一条直线上时,求BF的长;(3)、连接DF,若的面积为3,请直接写出BF的长.25. 如图,抛物线与x轴相交于点 , , 与y轴相交于点 , 抛物线的对称轴与x轴相交于点D,点E是x轴下方抛物线上的一个动点(点E,D,C不在同一条直线上),分别过点A,B作直线CE的垂线,垂足分别为M,N,连接MD,ND. (1)、求抛物线的解析式;(2)、延长MD交于BN点F,
(1)、求抛物线的解析式;(2)、延长MD交于BN点F,①求证:;
②求证:;
(3)、当为等边三角形时,请直接写出直线CE与抛物线对称轴的交点坐标.