辽宁省沈阳市皇姑区2022年中考一模数学试题
试卷更新日期:2022-07-06 类型:中考模拟
一、单选题
-
1. 下列各数中,既不是正数也不是负数的是( )A、0 B、-(-1) C、- D、22. 已知地球与月球间的平均距离约为38.44万公里,其中38.44万用科学记数法表示为( )A、 B、 C、 D、3. 如图,是由两个相同的小正方体和一个圆锥体组成的立体图形,其左视图是( )
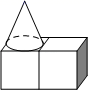 A、
A、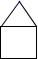 B、
B、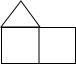 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在阴影部分的概率是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在阴影部分的概率是( ) A、 B、 C、 D、6. 某数学兴趣小组为了了解本班同学一周课外阅途的时间,随机调查了5名同学,并将所得数据整理如下表:
A、 B、 C、 D、6. 某数学兴趣小组为了了解本班同学一周课外阅途的时间,随机调查了5名同学,并将所得数据整理如下表:学生编号
1
2
3
4
5
一周课外阅读时间《小时》
7
5
4
□
8
表中有一个数字被污染后而模糊不清(该处用□表示),但曾计算得该组数据的平均数为6.则这组数数的方差和中位数分别为( )
A、1,5.4 B、2,4 C、2,6 D、6,67. 如图,已知A,B、C,D、E是⊙O上的五个点,圆心O在AD上,∠BCD=110°,则∠AEB的度数为( )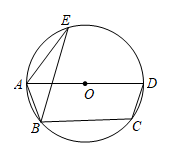 A、70° B、35° C、40° D、20°8. 一张小凳子的结构如图所示,AB∥CD,∠1=∠2= , AD=50厘米,则小凳子的高度MN为( )
A、70° B、35° C、40° D、20°8. 一张小凳子的结构如图所示,AB∥CD,∠1=∠2= , AD=50厘米,则小凳子的高度MN为( )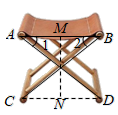 A、50厘米 B、厘米 C、50sin厘米 D、厘米9. 《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、10. 已知一次函数与反比例函数的图象在第二象限有两个交点,且其中一个交点的横坐标为-1,则二次函数的图象可能是( )A、
A、50厘米 B、厘米 C、50sin厘米 D、厘米9. 《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、10. 已知一次函数与反比例函数的图象在第二象限有两个交点,且其中一个交点的横坐标为-1,则二次函数的图象可能是( )A、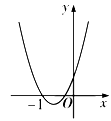 B、
B、 C、
C、 D、
D、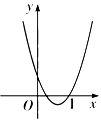
二、填空题
-
11. 分解因式: .12. 不等式的解集是.13. 如图,将一个正八边形与一个正六边形如图放置,顶点A、B、C、D四点共线,E为公共顶点.则∠FEG= .
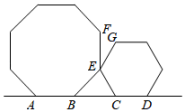 14. 如图所示,AB∥EF,∠B=35°,∠E=25°,则∠C+∠D的值为
14. 如图所示,AB∥EF,∠B=35°,∠E=25°,则∠C+∠D的值为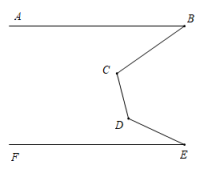 15. 如图,正比例函数的图象与反比例函数的图象在第一象限交于点A,将线段沿x轴向右平移3个单位长度得到线段 , 其中点A与点对应,若的中点B恰好也在该反比例函数图象上,则k的值为 .
15. 如图,正比例函数的图象与反比例函数的图象在第一象限交于点A,将线段沿x轴向右平移3个单位长度得到线段 , 其中点A与点对应,若的中点B恰好也在该反比例函数图象上,则k的值为 .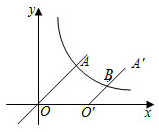 16. 在矩形ABCD中,AB=4,BC=3,点P在AB上.若将△DAP沿DP折叠,使点A落在矩形对角线上的A′处,则AP的长为 .
16. 在矩形ABCD中,AB=4,BC=3,点P在AB上.若将△DAP沿DP折叠,使点A落在矩形对角线上的A′处,则AP的长为 .
三、解答题
-
17. 计算:.18. 在新冠疫情的背景下,学校开设了空中课堂,学生要面对电脑等电子产品上网课,保护视力显得更加重要.某校经调查发现 , 两名女生和 , 两名男生对视力“非常重视”,若从这四人中随机抽取两人向全校作视力保护经验交流,请用“列表法”或“树状图法”求恰好抽到同性别学生的概率.19. 如图,在五边形ABCDE中,AB=CD,∠ABC=∠BCD,BE,CE分别是∠ABC,∠BCD的角平分线.
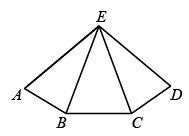 (1)、求证:△ABE≌△DCE;(2)、当∠A=80°,∠ABC=140°,时,∠AED=度(直接填空).20. 某中学为了解九年级学生的体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,请根据下面的两幅统计图回答下列问题:
(1)、求证:△ABE≌△DCE;(2)、当∠A=80°,∠ABC=140°,时,∠AED=度(直接填空).20. 某中学为了解九年级学生的体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,请根据下面的两幅统计图回答下列问题: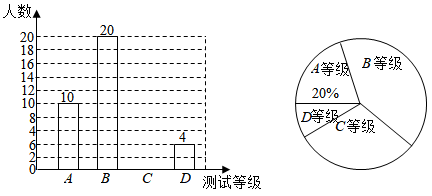 (1)、本次抽样调查共抽取了多少名学生?(2)、直接在图中将条形统计图补充完整;(3)、若该中学九年级共有700名学生,请你估计体能测试结果为D等级的学生有多少名.21. 在防疫新型冠状病毒期间,市民对医用口罩的需求越来越大,某药店第一次用3000元购进医用口罩若干个,第二次又用3000元购进该款口罩,但第二次每个口罩的进价是第一次进价的1.25倍,购进的数量比第一次少200个,求第一次购进医用口罩多少个?22. 如图,AB为⊙O的直径,CD是⊙O的弦,点E在AB的延长线上,连接OC、AD,CD∥AB。CO∥DE,∠A=22.5°.
(1)、本次抽样调查共抽取了多少名学生?(2)、直接在图中将条形统计图补充完整;(3)、若该中学九年级共有700名学生,请你估计体能测试结果为D等级的学生有多少名.21. 在防疫新型冠状病毒期间,市民对医用口罩的需求越来越大,某药店第一次用3000元购进医用口罩若干个,第二次又用3000元购进该款口罩,但第二次每个口罩的进价是第一次进价的1.25倍,购进的数量比第一次少200个,求第一次购进医用口罩多少个?22. 如图,AB为⊙O的直径,CD是⊙O的弦,点E在AB的延长线上,连接OC、AD,CD∥AB。CO∥DE,∠A=22.5°.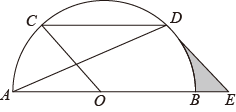 (1)、求证:DE是⊙O的切线;(2)、当时,图中阴影部分的周长为(直接填空).23. 如图,在平面直角坐标系中,直线AB与y轴交于点A,与x轴交于点B,BO=2OA.点N在线段OB上,过点N作NM⊥AB于M.当动点D从点A匀速运动到点M时,动点E恰好从点B匀速运动到点O;当点D运动到线段AM中点时,动点E恰好运动到点N.设 , , 且.
(1)、求证:DE是⊙O的切线;(2)、当时,图中阴影部分的周长为(直接填空).23. 如图,在平面直角坐标系中,直线AB与y轴交于点A,与x轴交于点B,BO=2OA.点N在线段OB上,过点N作NM⊥AB于M.当动点D从点A匀速运动到点M时,动点E恰好从点B匀速运动到点O;当点D运动到线段AM中点时,动点E恰好运动到点N.设 , , 且.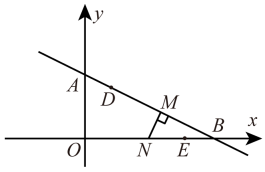 (1)、求线段OA的长;(2)、求线段BM的长;(3)、连接DE,当△DEB的面积最大时,直接写出x的值.24. 已知,在△ABC中,AB=BC,∠ABC=90°,点D在射线CB上,连接DA.将线段DA绕点D逆时针旋转90°后得到DE,过点E作EM⊥BC交直线BC于点M,连接AE,CE.
(1)、求线段OA的长;(2)、求线段BM的长;(3)、连接DE,当△DEB的面积最大时,直接写出x的值.24. 已知,在△ABC中,AB=BC,∠ABC=90°,点D在射线CB上,连接DA.将线段DA绕点D逆时针旋转90°后得到DE,过点E作EM⊥BC交直线BC于点M,连接AE,CE.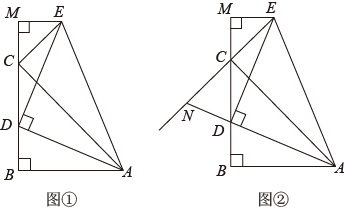 (1)、当点D在线段CB上(且不与点C,点B重合)时,如图①所示.
(1)、当点D在线段CB上(且不与点C,点B重合)时,如图①所示.①求证:MC=BD;
②求证:∠ACE=90°;
(2)、延长AD与直线CE相交于点N.①当点D在线段CB上(且不与点C,点B重合)时,如图②所示.若AD平分∠BAC,且 , 直接写出线段NE的长;
②当时,直接写出的值.
25. 在平面直角坐标系中,直线与x轴交于A,与y轴交于点B,抛物线过点A和点B,且与x轴交于另一点C,点D为抛物线的顶点,点P是抛物线上一动点,过点P作PE⊥x轴于点E,设点P的横坐标为m.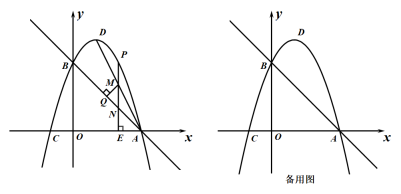 (1)、求抛物线的解析式;(2)、如图,连接DA,当点P在直线DA右上方的抛物线上时,PE交DA于点M,过点M作MQ⊥AB于点Q,若MQ= , 求m的值;(3)、连接CB,当点P在第四象限的抛物线上时,以OB,OE为边作矩形BOEF,点H在线段OE上,过点H作HG∥EF交直线BF于点G,过点F作FK⊥BC交射线CB于点K,连接KG,KH,若△KGF和△KGH相似,直接写出m的值.
(1)、求抛物线的解析式;(2)、如图,连接DA,当点P在直线DA右上方的抛物线上时,PE交DA于点M,过点M作MQ⊥AB于点Q,若MQ= , 求m的值;(3)、连接CB,当点P在第四象限的抛物线上时,以OB,OE为边作矩形BOEF,点H在线段OE上,过点H作HG∥EF交直线BF于点G,过点F作FK⊥BC交射线CB于点K,连接KG,KH,若△KGF和△KGH相似,直接写出m的值.