辽宁省沈阳市和平区2022年九年级中考一模数学试卷
试卷更新日期:2022-07-06 类型:中考模拟
一、单选题
-
1. 如图是由五个相同的小立方块搭成的几何体,这个几何体的俯视图是( )
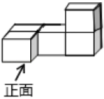 A、
A、 B、
B、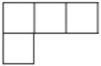 C、
C、 D、
D、 2. 下列各点中,不在反比例函数的图象上的是( )A、 B、 C、 D、3. 已知直线 , 一块直角三角尺如图放置,其中 , , 若 , 则的度数是( )
2. 下列各点中,不在反比例函数的图象上的是( )A、 B、 C、 D、3. 已知直线 , 一块直角三角尺如图放置,其中 , , 若 , 则的度数是( ) A、20° B、25° C、30° D、35°4. 下列,图形中,是轴对称而不是中心对称图形是( )A、等边三角形 B、矩形 C、平行四边形 D、菱形5. 若这个数介于整数n和之间,则的值是( )A、0 B、1 C、2 D、36. 如图,已知线段AB=4,利用尺规作AB的垂直平分线,步骤如下:①分别以点A和点B为圆心,以一定长度m为半径作弧,两弧相交于点C和点D;②作直线CD,直线CD就是线段AB的垂直平分线.下列各数中,m的值可能是( )
A、20° B、25° C、30° D、35°4. 下列,图形中,是轴对称而不是中心对称图形是( )A、等边三角形 B、矩形 C、平行四边形 D、菱形5. 若这个数介于整数n和之间,则的值是( )A、0 B、1 C、2 D、36. 如图,已知线段AB=4,利用尺规作AB的垂直平分线,步骤如下:①分别以点A和点B为圆心,以一定长度m为半径作弧,两弧相交于点C和点D;②作直线CD,直线CD就是线段AB的垂直平分线.下列各数中,m的值可能是( ) A、1 B、1.5 C、2 D、2.57. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定8. 根据某商场去年四个季度的营业额绘制成如图所示的扇形统计图,根据统计图判断下列说法中,正确的是( )
A、1 B、1.5 C、2 D、2.57. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定8. 根据某商场去年四个季度的营业额绘制成如图所示的扇形统计图,根据统计图判断下列说法中,正确的是( ) A、一季度营业额占总营业额的30% B、二季度营业额占总营业额的20% C、三季度营业额在统计图中所对应的圆心角的度数是20° D、四季度营业额占总营业额的一半9. 2021年国内生产总值达到元,数据可以表示为( )A、1.14万亿 B、11.4万亿 C、114万亿 D、1140万亿10. 如图,矩形ABCD中,对角线AC,BD相交于点E,BF∥AC,CF∥BD,若四边形BECF面积为1,则矩形ABCD的面积为( )
A、一季度营业额占总营业额的30% B、二季度营业额占总营业额的20% C、三季度营业额在统计图中所对应的圆心角的度数是20° D、四季度营业额占总营业额的一半9. 2021年国内生产总值达到元,数据可以表示为( )A、1.14万亿 B、11.4万亿 C、114万亿 D、1140万亿10. 如图,矩形ABCD中,对角线AC,BD相交于点E,BF∥AC,CF∥BD,若四边形BECF面积为1,则矩形ABCD的面积为( ) A、1 B、2 C、4 D、8
A、1 B、2 C、4 D、8二、填空题
-
11. 因式分解: .12. 一次函数y=kx+b满足kb>0,且函数值y随自变量x的增大而增大,则此函数的图象不经过第象限.13. 已知圆的周长是 , 则该圆的内接正三角形的边心距是 .14. 若 , , 则的值为 .15. 函数中,自变量x的取值范围是 .16. 正方形ABCD的边长为2,点E在边BC上,将△CDE沿直线DE翻折,使点C落在正方形内的点F处,连接BF并延长交正方形ABCD一边于点G.当时,则CE的长为 .

三、解答题
-
17. 计算: .18. 到目前为止,北京是世界上唯一一个既举办过夏季奥运会,又举办过冬季奥运会的城市,小明是个集邮爱好者,他收集了如图所示的四张纪念邮票(除正面内容不同外,其余均相同),现将四张邮票背面朝上,洗匀放好.
 (1)、小明从中随机抽取一张邮票是冬奥会吉祥物冰墩墩的概率是;(2)、小明从中随机抽取一张邮票,记下邮票正面内容后,放回后洗匀,四张邮票背面朝上,再从中随机抽取一张邮票,记下邮票正面内容,请用列表法或画树状图法,求小明两次抽取的邮票中至少有一张是冬奥会吉祥物冰墩墩的概率.(这四张邮票依次分别用字母A,B,C,D表示)19. 如图,在平行四边形ABCD中,以A为圆心,AB长为半径画弧交AD于点F;再分别以B,F为圆心,大于的长为半径作弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.
(1)、小明从中随机抽取一张邮票是冬奥会吉祥物冰墩墩的概率是;(2)、小明从中随机抽取一张邮票,记下邮票正面内容后,放回后洗匀,四张邮票背面朝上,再从中随机抽取一张邮票,记下邮票正面内容,请用列表法或画树状图法,求小明两次抽取的邮票中至少有一张是冬奥会吉祥物冰墩墩的概率.(这四张邮票依次分别用字母A,B,C,D表示)19. 如图,在平行四边形ABCD中,以A为圆心,AB长为半径画弧交AD于点F;再分别以B,F为圆心,大于的长为半径作弧,两弧交于点P;连接AP并延长交BC于点E,连接EF. (1)、求证:四边形ABEF是菱形;(2)、若菱形ABEF的周长为4, , 则请直接写出的大小为 .20. 为了了解某射击队中各队员的射击水平,从中随机抽取甲、乙两名队员10次射击训练成绩,将获得的数据整理绘制成不完整的统计图.
(1)、求证:四边形ABEF是菱形;(2)、若菱形ABEF的周长为4, , 则请直接写出的大小为 .20. 为了了解某射击队中各队员的射击水平,从中随机抽取甲、乙两名队员10次射击训练成绩,将获得的数据整理绘制成不完整的统计图.
教练又根据甲、乙两名队员射击成绩绘制了数据分析表:
选手
平均数/环
中位数/环
众数/环
方差
甲
8
8
8
c
乙
7.5
a
b
2.65
根据图表中提供的信息,请解答下列问题:
(1)、在答题卡上直接补全条形统计图;(2)、请直接写出a= , b= , c= .21. 小明家距学校980m.(1)、若他从家跑步上学,路上时间不超过490s,请直接写出小明跑步的平均速度至少为m/s.(2)、若他从家出发,先步行了350m后,发现上学要迟到了,因此换骑上了共享单车,达到学校时,全程共花了480s.已知小明骑共享单车的平均速度是步行平均速度的3倍,求小明骑共享单车的平均速度是多少?(转换出行方式时,所需时间忽略不计,假设家到学校随时都有共享单车).22. 如图,AB是的直径,点C是圆上一点,连接AC,BC, . 且 . (1)、求证:CD是的切线;(2)、若 , , 求图中阴影部分的面积(结果保留).23. 如图,在平面直角坐标系中,点A坐标为 , 点B坐标为 , 直线AB与y轴交于点C.
(1)、求证:CD是的切线;(2)、若 , , 求图中阴影部分的面积(结果保留).23. 如图,在平面直角坐标系中,点A坐标为 , 点B坐标为 , 直线AB与y轴交于点C. (1)、求直线AB的函数表达式及线段AC的长;(2)、点B关于y轴的对称点为点D.
(1)、求直线AB的函数表达式及线段AC的长;(2)、点B关于y轴的对称点为点D.①请直接写出点D的坐标为;
②在直线BD上找点E,使△ACE是直角三角形,请直接写出点E的横坐标为 .
24. 如图,在Rt△ABC中, , , , 将△ABC沿CB方向平移得到△DEF. (1)、当△ABC与△DEF重叠部分的面积是△ABC面积一半时,求△ABC平移的距离;(2)、当DF的中点M恰好落在的平分线上时,
(1)、当△ABC与△DEF重叠部分的面积是△ABC面积一半时,求△ABC平移的距离;(2)、当DF的中点M恰好落在的平分线上时,①求△ABC平移距离;
②将△DEF绕点E旋转后得到△GEH(点D的对应点是点G,点F对应点是点H),在旋转过程中,直线GH与直线AB交于点K,与直线AC交于点J,当△AKJ是以AJ为底边的等腰三角形时,请直接写出此时AJ的长为 .
25. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B.抛物线经过点A、点B. (1)、求抛物线的函数表达式并直接写出顶点的坐标;(2)、若在第三象限的抛物线上有一动点M,当点M到直线AB的距离最大时,求点M的坐标;(3)、点C,D分别为线段AO,线段AB上的点,且 , 连接CD.将线段CD绕点D顺时针旋转90度,点C旋转后的对应点为点E,连接OE.当线段OE的长最小时,请直接写出直线DE的函数表达式 .
(1)、求抛物线的函数表达式并直接写出顶点的坐标;(2)、若在第三象限的抛物线上有一动点M,当点M到直线AB的距离最大时,求点M的坐标;(3)、点C,D分别为线段AO,线段AB上的点,且 , 连接CD.将线段CD绕点D顺时针旋转90度,点C旋转后的对应点为点E,连接OE.当线段OE的长最小时,请直接写出直线DE的函数表达式 .