辽宁省大连市2022年中考一模数学试题
试卷更新日期:2022-07-06 类型:中考模拟
一、单选题
-
1. 一5的绝对值是( )A、5 B、 C、 D、-52. 下列立体图形中,主视图是三角形的是( )A、
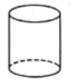 B、
B、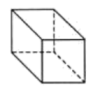 C、
C、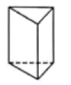 D、
D、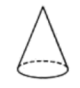 3. 在平面直角坐标系中,点P(2,-3)向右平移1个单位长度,得到点P',则点P'的坐标为( )A、(1,-3) B、(2,-4) C、(3,-3) D、(2,-2)4. 下列图形中既是轴对称图形又是中心对称图形的是( )A、等边三角形 B、正五边形 C、平行四边形 D、正方形5. 2022年3月5日,第十三届人大五次会议在人民大会堂开幕会上,提请会议审议的政府工作报告提出,2022年城镇新增就业目标为1100万人以上,将11000000用科学记数法表示应为( )A、11×106 B、1.1×107 C、0.11×108 D、1.1×1086. 下列计算正确的是( )A、 B、 C、 D、7. 下表是某公司员工月收入的资料.
3. 在平面直角坐标系中,点P(2,-3)向右平移1个单位长度,得到点P',则点P'的坐标为( )A、(1,-3) B、(2,-4) C、(3,-3) D、(2,-2)4. 下列图形中既是轴对称图形又是中心对称图形的是( )A、等边三角形 B、正五边形 C、平行四边形 D、正方形5. 2022年3月5日,第十三届人大五次会议在人民大会堂开幕会上,提请会议审议的政府工作报告提出,2022年城镇新增就业目标为1100万人以上,将11000000用科学记数法表示应为( )A、11×106 B、1.1×107 C、0.11×108 D、1.1×1086. 下列计算正确的是( )A、 B、 C、 D、7. 下表是某公司员工月收入的资料.月收入/元
10000
8000
5600
5000
3400
3000
人数
1
1
3
6
7
2
则此公司全体员工月收入的中位数为( )
A、5300元 B、5000元 C、4730元 D、3400元8. 一次函数y=-2x+4的图象与x轴的交点坐标是( )A、(-2,0) B、( , 0) C、(2,0) D、(0,4)9. 如图,∠AOB=40°,以点O为圆心,适当长为半径画弧,交OA,OB于C,D两点,分别以C,D为圆心,大于CD的长为半径画弧,两弧在∠AOB的内部相交于点E,画射线OE,过点E作OB的平行线交OA于点F,则∠OEF的度数为( ) A、20° B、30° C、40° D、140°10. 在某圆形喷水池的池中心竖直安装一根水管,在水管的顶端安一个喷水头,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,建立如图所示的平面直角坐标系,若喷出的抛物线形水柱解析式为(0≤x≤3),则水管长为( )
A、20° B、30° C、40° D、140°10. 在某圆形喷水池的池中心竖直安装一根水管,在水管的顶端安一个喷水头,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,建立如图所示的平面直角坐标系,若喷出的抛物线形水柱解析式为(0≤x≤3),则水管长为( )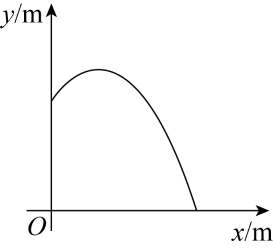 A、1m B、2m C、m D、3m
A、1m B、2m C、m D、3m二、填空题
-
11. 不等式2x-1>0的解集为.12. 方程 的解为.13. 不透明袋子中装有5个红球,3个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .14. 如图,在△ABC中,DE是AC的垂直平分线,AE=3,△ABD的周长为13,则△ABC的周长为.
 15. 如图,在菱形ABCD中,AB=4,∠ABC=60°,对角线AC,BD交于点O,分别以点A,C为圆心,AO的长为半径画弧,与该菱形的边相交,则图中阴影部分的面积为.
15. 如图,在菱形ABCD中,AB=4,∠ABC=60°,对角线AC,BD交于点O,分别以点A,C为圆心,AO的长为半径画弧,与该菱形的边相交,则图中阴影部分的面积为. 16. 如图,用大小相同的小正方形拼图形,第1个图形是一个小正方形;第2个图形由9个小正方形拼成;第3个图形由25个小正方形拼成,依此规律,若第n个图形比第(n-1)个图形多用了72个小正方形,则n的值是.
16. 如图,用大小相同的小正方形拼图形,第1个图形是一个小正方形;第2个图形由9个小正方形拼成;第3个图形由25个小正方形拼成,依此规律,若第n个图形比第(n-1)个图形多用了72个小正方形,则n的值是.
三、解答题
-
17. 计算18. 为了解某校九年级学生周末学习时长情况,随机抽取该年级部分学生进行调查,以下是根据调查结果绘制的统计图表的一部分.
学习时长x(小时)
人数
频率
4<x≤5
2
b
5<x≤6
a
0.3
6<x≤7
c
7<x≤8
0.2

根据以上信息,回答下列问题:
(1)、填空:a= , b= , c=;(2)、若该校九年级共有1000名学生,请估计学习时长在5<x≤7范围内的学生人数.19. 第24届北京冬奥会冰壶混合双人循环赛在冰立方举行.参加比赛的每两队之间都进行一场比赛,共要比赛45场,共有多少个队参加比赛?20. 如图,在平行四边形ABCD中,连接AC,BE⊥AC,DF⊥AC,垂足分别为E, F,连接DE,BF.求证:四边形BFDE是平行四边形. 21. 如图,平面直角坐标系中,正方形ABCD的顶点B,C在x轴上,反比例函数(x>0)的图象经过点A(1,3),交CD于点E.
21. 如图,平面直角坐标系中,正方形ABCD的顶点B,C在x轴上,反比例函数(x>0)的图象经过点A(1,3),交CD于点E. (1)、求该反比例函数的解析式:(2)、求△BCE的面积.22. 如图1,AB是⊙O的直径,C,D是⊙O上的点,连接CB,CD,延长CA,BD交于点E,∠BDC=2∠ABE.
(1)、求该反比例函数的解析式:(2)、求△BCE的面积.22. 如图1,AB是⊙O的直径,C,D是⊙O上的点,连接CB,CD,延长CA,BD交于点E,∠BDC=2∠ABE. (1)、求证:AE=AB;(2)、如图2,过点D作⊙O的切线交AE于点F,若DF= , CD= , 求EF长.23. 如图,大连森林动物园浪漫之星摩天轮是大连市著名建筑之一.已知摩天轮是一个圆形,匀速旋转一周需20分钟.小明测得摩天轮上A处顺时针旋转到B处需6分钟,且这两处到地面的距离(AC和BD)都恰好为64米,OF上MN交⊙O于点E,EF=8米.
(1)、求证:AE=AB;(2)、如图2,过点D作⊙O的切线交AE于点F,若DF= , CD= , 求EF长.23. 如图,大连森林动物园浪漫之星摩天轮是大连市著名建筑之一.已知摩天轮是一个圆形,匀速旋转一周需20分钟.小明测得摩天轮上A处顺时针旋转到B处需6分钟,且这两处到地面的距离(AC和BD)都恰好为64米,OF上MN交⊙O于点E,EF=8米.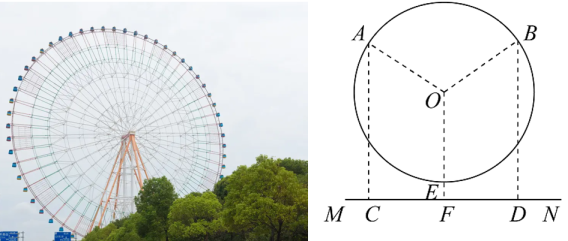 (1)、劣弧AB所对的圆心角度数为°;(2)、请您帮助小明估算摩天轮的半径(结果取整数).
(1)、劣弧AB所对的圆心角度数为°;(2)、请您帮助小明估算摩天轮的半径(结果取整数).(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38)
24. 如图,在Rt△ACB中,∠ACB=90°,AC=3cm,BC=4cm.点D在边AB上,AD=AC,DEBC,垂足为E,点P从点C出发,以2cm/s的速度沿边CB运动,当点P与点B重合时,停止运动.过点P作BC的垂线,交射线CD于点F.设点P的运动时间为t(s),△CPF与△DCB重叠部分图形面积为S(cm²). (1)、请直接写出AB的长;(2)、求CE的长;(3)、求S关于t的函数解析式,并直接写出自变量t的取值范围.25. 如图1,四边形ABCD中,AB=AD,∠BAD=90°,∠D=90°+∠C,点E,F分别在边BC,AD上,∠BAE=∠AEF,EB=EF.
(1)、请直接写出AB的长;(2)、求CE的长;(3)、求S关于t的函数解析式,并直接写出自变量t的取值范围.25. 如图1,四边形ABCD中,AB=AD,∠BAD=90°,∠D=90°+∠C,点E,F分别在边BC,AD上,∠BAE=∠AEF,EB=EF. (1)、猜想∠B与∠C的数量关系,并证明;(2)、求证:BC=AB+AF;(3)、如图2,若AF=1,AB=2,AF>CD,求CD的长.26. 抛物线y1=x2+(3-m)x+c与直线l:y2=kx+b分别交于点A(-2,0)和点B(m,n),当-2≤x≤4时,y1≤y2 .(1)、求c和n的值(用含m的式子表示);(2)、过点P(1,0)作x轴的垂线,分别交抛物线和直线l于M,N两点,则△BMN的面积是否存在最大值或者最小值,若存在,请求出这个值;若不存在,请说明理由;(3)、直线x=m+1交抛物线于点C,过点C作x轴的平行线交直线l于点D,交抛物线另一点于E,连接BE,求∠DBE的度数.
(1)、猜想∠B与∠C的数量关系,并证明;(2)、求证:BC=AB+AF;(3)、如图2,若AF=1,AB=2,AF>CD,求CD的长.26. 抛物线y1=x2+(3-m)x+c与直线l:y2=kx+b分别交于点A(-2,0)和点B(m,n),当-2≤x≤4时,y1≤y2 .(1)、求c和n的值(用含m的式子表示);(2)、过点P(1,0)作x轴的垂线,分别交抛物线和直线l于M,N两点,则△BMN的面积是否存在最大值或者最小值,若存在,请求出这个值;若不存在,请说明理由;(3)、直线x=m+1交抛物线于点C,过点C作x轴的平行线交直线l于点D,交抛物线另一点于E,连接BE,求∠DBE的度数.