吉林省长春市南关区2022年第一次模拟数学试题
试卷更新日期:2022-07-06 类型:中考模拟
一、单选题
-
1. 的值为( )A、 B、3 C、 D、2. 2021年5月11日,第七次全国人口普查结果公布,我国总人口大约为1412000000人,把数字1412000000用科学记数法表示为( )A、14.12×108 B、1.412×1010 C、0.1412×1010 D、1.412×1093. 如图是一个立体图形的三视图,这个立体图形是( ).
 A、圆柱 B、圆锥 C、长方体 D、三棱柱4. 关于x的一元二次方程没有实数根,则m的值可能是( )A、 B、0 C、1 D、5. 如图,某飞机于空中A处探测到正下方的地面目标C,此时飞机高度AC为1200米,从飞机上看地面控制点B的俯角为 , 则B、C之间的距离为( )
A、圆柱 B、圆锥 C、长方体 D、三棱柱4. 关于x的一元二次方程没有实数根,则m的值可能是( )A、 B、0 C、1 D、5. 如图,某飞机于空中A处探测到正下方的地面目标C,此时飞机高度AC为1200米,从飞机上看地面控制点B的俯角为 , 则B、C之间的距离为( ) A、米 B、米 C、米 D、米6. 如图,直线 , 点A在EF上,点B、C在MN上,点D在线段AC上.若 , , 则的大小为( )
A、米 B、米 C、米 D、米6. 如图,直线 , 点A在EF上,点B、C在MN上,点D在线段AC上.若 , , 则的大小为( ) A、50° B、110° C、120° D、140°7. 如图,在中, , . 用无刻度的直尺和圆规在AB边上找一点D,使 , 则符合要求的作图是( )A、
A、50° B、110° C、120° D、140°7. 如图,在中, , . 用无刻度的直尺和圆规在AB边上找一点D,使 , 则符合要求的作图是( )A、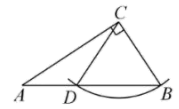 B、
B、 C、
C、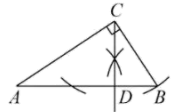 D、
D、 8. 如图,在平面直角坐标系中,的顶点B、C在x轴的正半轴上, , 点D在AB边上,且 , 函数的图象经过点D.若点A、B的坐标分别为、 , 则k的值为( )
8. 如图,在平面直角坐标系中,的顶点B、C在x轴的正半轴上, , 点D在AB边上,且 , 函数的图象经过点D.若点A、B的坐标分别为、 , 则k的值为( ) A、 B、3 C、4 D、
A、 B、3 C、4 D、二、填空题
-
9. 化简: .10. 分解因式: .11. 不等式组的解集为 .12. 正六边形的每一个外角是度13. 如图,菱形ABCD的对角线AC与BD相交于点O,分别以点A、C为圆心,OA长为半径作、交AD于点E、BC于点F.若 , , 则阴影部分图形的面积为 . (结果保留)
 14. 如图,在平面直角坐标系中,抛物线与y轴交于点A,过点A作x轴的平行线交抛物线于点B、C,则线段BC的长为 .
14. 如图,在平面直角坐标系中,抛物线与y轴交于点A,过点A作x轴的平行线交抛物线于点B、C,则线段BC的长为 .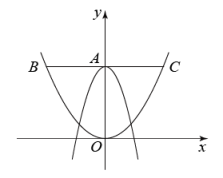
三、解答题
-
15. 先化简,再求值: , 其中 .16. 一个不透明的口袋中装有2个黄球、1个白球,每个小球除颜色不同外其余均相同.从口袋中随机摸出1个小球,记下颜色后放回并搅匀,再从口袋中随机摸出一个小球.用画树状图(或列表)的方法,求两次摸出的球至少有一个白球的概率.17. 为保障新冠病毒疫苗接种需求,某生物科技公司开启“加速”模式,生产效率提高到原来的1.2倍,现在生产480万剂疫苗所用的时间比原来生产440万剂疫苗所用的时间少1天.求原来每天生产多少万剂疫苗?18. 如图,AB是的直径,BC切于点B,AC交于点D.已知的半径为9, .
 (1)、求的度数.(2)、求的长,(结果保留)19. 为了解学生掌握垃圾分类知识的情况,某学校举行了“垃圾分类人人有责”知识竞赛活动.活动结束后,从该校七、八年级中各随机抽取20名学生的竞赛成绩(百分制),并对成绩进行了整理和描述,下面给出了部分信息:
(1)、求的度数.(2)、求的长,(结果保留)19. 为了解学生掌握垃圾分类知识的情况,某学校举行了“垃圾分类人人有责”知识竞赛活动.活动结束后,从该校七、八年级中各随机抽取20名学生的竞赛成绩(百分制),并对成绩进行了整理和描述,下面给出了部分信息:Ⅰ.八年级学生竞赛成绩如下:
81 92 84 95 85 95 88 99 89 100
92 83 93 84 95 87 99 89 90 100
Ⅱ.七、八年级各20名学生竞赛成绩的频数分布统计表如下:
七年级
4
6
2
8
八年级
4
a
4
7
Ⅲ.七、八年级各20名学生竞赛成绩的平均数、众数、中位数如下:
平均数
众数
中位数
七年级
91
96
89
八年级
91
m
n
根据以上信息,回答下列问题:
(1)、表中a的值为 , m的值为 , n的值为 .(2)、在抽取的七、八年级学生中,若七年级甲同学和八年级乙同学分数都为90分,同学的分数在本年级抽取的学生分数中从高到低排序更靠前,(填“甲”或“乙”)(3)、根据抽查结果,求该校450名七年级学生竞赛成绩不低于95分的人数.20. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,线段AB、BC的端点均在格点上,只用无刻度的直尺,在给定的网格中按下列要求以AB、BC为邻边画四边形,使第四个顶点在格点上. (1)、在图①中画一个中心对称的四边形ABCD.(2)、在图②中画一个轴对称的四边形ABCE.(3)、在图③中画一个非轴对称的四边形ABCF,且使 .21. 如图①,我国传统计重工具杆秤的应用方便了人们的生活.某兴趣小组为探究秤杆上秤砣到秤纽的水平距离x厘米()与秤钩所挂物体重量y斤之间的关系,进行了6次称重,下表为称重时所记录的一些数据.
(1)、在图①中画一个中心对称的四边形ABCD.(2)、在图②中画一个轴对称的四边形ABCE.(3)、在图③中画一个非轴对称的四边形ABCF,且使 .21. 如图①,我国传统计重工具杆秤的应用方便了人们的生活.某兴趣小组为探究秤杆上秤砣到秤纽的水平距离x厘米()与秤钩所挂物体重量y斤之间的关系,进行了6次称重,下表为称重时所记录的一些数据.x
4
12
16
24
28
36
y
0
1
1.5
2.5
3
4
 (1)、在图②的平面直角坐标系中,描出以表格中x的值为横坐标、y的值为纵坐标的各点.(2)、观察(1)所描各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式.(3)、当秤杆上秤砣到秤纽的水平距离为40厘米时,求秤钩所挂物体的重量.(4)、若这个秤最大的秤重量是6斤,直接写出秤砣到秤纽的水平距离x的取值范围.22. 实践与探究
(1)、在图②的平面直角坐标系中,描出以表格中x的值为横坐标、y的值为纵坐标的各点.(2)、观察(1)所描各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式.(3)、当秤杆上秤砣到秤纽的水平距离为40厘米时,求秤钩所挂物体的重量.(4)、若这个秤最大的秤重量是6斤,直接写出秤砣到秤纽的水平距离x的取值范围.22. 实践与探究如图①,在矩形ABCD中, , . 将矩形ABCD沿过点A的直线折叠,使点D落在矩形ABCD的内部,点D的对应点为点 , 折痕为AE,再将矩形ABCD沿过点A的直线折叠,使点B落在边上,折痕为AF,点B的对应点为点 . 延长交AE于点G,过点G作直线交AD于点M,交BC于点N.
 (1)、求证: .(2)、求证:四边形ABNM是正方形.(3)、若 , 求线段BF的长.(4)、如图②,将矩形沿所在直线继续折叠,点C的对应点为点 . 我们发现,点E的位置不同,点的位置也不同.当点恰好与点重合时,线段DE的长为 .23. 如图,在中, , , . 动点P从点B出发沿折线BC—CA以每秒5个单位长度的速度向终点A运动,当点P不与的顶点重合时,过点P作于点D,以PD为直角边构造等腰直角三角形PDE,使 , 且点E、点C始终在PD的同侧,设点P运动的时间为t秒.
(1)、求证: .(2)、求证:四边形ABNM是正方形.(3)、若 , 求线段BF的长.(4)、如图②,将矩形沿所在直线继续折叠,点C的对应点为点 . 我们发现,点E的位置不同,点的位置也不同.当点恰好与点重合时,线段DE的长为 .23. 如图,在中, , , . 动点P从点B出发沿折线BC—CA以每秒5个单位长度的速度向终点A运动,当点P不与的顶点重合时,过点P作于点D,以PD为直角边构造等腰直角三角形PDE,使 , 且点E、点C始终在PD的同侧,设点P运动的时间为t秒. (1)、用含t的代数式表示线段PC的长.(2)、当点E落在AC边上时,求t的值.(3)、当点E在AB边垂直平分线上时,求t的值.(4)、连结CE,当为锐角时,直接写出t的取值范围.24. 在平面直角坐标系中,已知抛物线(m为常数且).(1)、当时,抛物线的顶点坐标为 .(2)、抛物线经过坐标原点时,求此抛物线所对应的二次函数的表达式,并写出函数值y随x的增大而增大时x的取值范围.(3)、当抛物线在直线和直线之间的部分(包括边界点)的最高点的纵坐标为5时,求m的值.(4)、点关于y轴的对称点为点D,点关于y轴的对称点为点C.当抛物线与四边形ABCD的边有两个交点,且两个交点到抛物线的对称轴的距离之和为3时,直接写出m的值.
(1)、用含t的代数式表示线段PC的长.(2)、当点E落在AC边上时,求t的值.(3)、当点E在AB边垂直平分线上时,求t的值.(4)、连结CE,当为锐角时,直接写出t的取值范围.24. 在平面直角坐标系中,已知抛物线(m为常数且).(1)、当时,抛物线的顶点坐标为 .(2)、抛物线经过坐标原点时,求此抛物线所对应的二次函数的表达式,并写出函数值y随x的增大而增大时x的取值范围.(3)、当抛物线在直线和直线之间的部分(包括边界点)的最高点的纵坐标为5时,求m的值.(4)、点关于y轴的对称点为点D,点关于y轴的对称点为点C.当抛物线与四边形ABCD的边有两个交点,且两个交点到抛物线的对称轴的距离之和为3时,直接写出m的值.