甘肃省酒泉市肃州区2022年中考适应性检测(一)数学试题
试卷更新日期:2022-07-06 类型:中考模拟
一、单选题
-
1. -2022的相反数是( )A、2022 B、-2022 C、 D、2. 冬季奥林匹克运动会是世界规模最大的冬季综合性运动会,每四年举办一次,第24届冬奥会将于2022年在北京和张家口举办.下列四个图分别是第24届冬奥会图标中的一部分,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食物和药物,得到广泛的使用.经测算,一粒芝麻的质量约为0.00000201kg,将0.00000201用科学记数法表示为( )A、 B、 C、 D、4. 下列计算结果为的是( )A、 B、 C、 D、5. 甲,乙,丙,丁四位男同学的5次足球30米S型绕杆运球的平均时间x(秒)及方差如下表所示,则这四名同学成绩最好的是( )
3. 芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食物和药物,得到广泛的使用.经测算,一粒芝麻的质量约为0.00000201kg,将0.00000201用科学记数法表示为( )A、 B、 C、 D、4. 下列计算结果为的是( )A、 B、 C、 D、5. 甲,乙,丙,丁四位男同学的5次足球30米S型绕杆运球的平均时间x(秒)及方差如下表所示,则这四名同学成绩最好的是( )甲
乙
丙
丁
x
9.5
9.5
10
10
0.2
0.45
0.2
0.45
A、甲 B、乙 C、丙 D、丁6. 将一个含有30°角的直角三角板和一把直尺按如图方式放置,若 , 则的度数为( ) A、120° B、125° C、130° D、135°7. 如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形ABCD,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线BE与边DC相交于点F,如果测得米,那么塔与树的距离AE为( )
A、120° B、125° C、130° D、135°7. 如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形ABCD,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线BE与边DC相交于点F,如果测得米,那么塔与树的距离AE为( ) A、15米 B、20米 C、25米 D、30米8. 为了能让更多人接种,某药厂的新冠疫苗生产线开足马力,24小时运转,该条生产线计划加工320万支疫苗,前5天按原计划的速度生产,5天后以原来速度的1.25倍生产,结果比原计划提前3天完成任务.设原计划每天生产 万支疫苗,则可列方程为( )A、 B、 C、 D、9. 如图,AB是的直径,CD是的弦,连接BD、BC,若 , 则的度数为( )
A、15米 B、20米 C、25米 D、30米8. 为了能让更多人接种,某药厂的新冠疫苗生产线开足马力,24小时运转,该条生产线计划加工320万支疫苗,前5天按原计划的速度生产,5天后以原来速度的1.25倍生产,结果比原计划提前3天完成任务.设原计划每天生产 万支疫苗,则可列方程为( )A、 B、 C、 D、9. 如图,AB是的直径,CD是的弦,连接BD、BC,若 , 则的度数为( ) A、34° B、56° C、68° D、102°10. 如图1,点P从 的顶点A出发,沿 匀速运动到点C,图2是点P运动时线段 的长度y随时间x变化的关系图象,其中点Q为曲线部分的最低点,则 的边 的长度为( )
A、34° B、56° C、68° D、102°10. 如图1,点P从 的顶点A出发,沿 匀速运动到点C,图2是点P运动时线段 的长度y随时间x变化的关系图象,其中点Q为曲线部分的最低点,则 的边 的长度为( ) A、12 B、8 C、10 D、13
A、12 B、8 C、10 D、13二、填空题
-
11. 因式分解 .12. 在数学实践课上,同学们进行投针试验:在平面上有一组平行线,相邻两条平行线间的距离都为5cm,将一根长度为3cm的针任意投掷在这个平面上,针可能与某一直线相交,也可能与任一直线都不相交,下表记录了他们的试验数据.
试验次数n
50
100
200
500
1000
2000
相交频数m
23
48
83
207
404
802
相交频率
0.460
0.480
0.415
0.414
0.404
0.401
若进行一次投针试验,估计针与直线相交的概率是(结果保留小数点后一位).
13. 要使分式 有意义,则x的取值范围为 .14. 若关于x的一元二次方程有实数根,则k的取值范围是 .15. 如图,在中, , , AD平分交BC于点D,点E、F分别是AD、AC的中点,则的度数为 . 16. 定义:如果三角形的一个内角是另一个内角的2倍,那么称这个三角形为“倍角三角形”,若一个等腰三角形恰好是“倍角三角形”,则它的顶角度数为 .17. 如图,在半圆O中, , 点C是的中点,则图中阴影部分的面积是 .
16. 定义:如果三角形的一个内角是另一个内角的2倍,那么称这个三角形为“倍角三角形”,若一个等腰三角形恰好是“倍角三角形”,则它的顶角度数为 .17. 如图,在半圆O中, , 点C是的中点,则图中阴影部分的面积是 . 18. 按一定规律排列的多项式: , , , , , …,根据上述规律,则第n个多项式是 .
18. 按一定规律排列的多项式: , , , , , …,根据上述规律,则第n个多项式是 .三、解答题
-
19. 计算:20. 化简求值: ,其中 .21. 如图,已知点D在△ABC的边AB上,且AD=CD,
 (1)、用直尺和圆规作∠BDC的平分线DE,交BC于点E(不写作法,保留作图痕迹);(2)、在(1)的条件下,判断DE与AC的位置关系,并写出证明过程.22. 敦煌莫高窟是中国现存规模最大、保存最为完好的佛教艺术宝库,被誉为“沙漠中的古代艺术画廊”,位于石窟群中段的红色楼阁(如图①),便是莫高窟标志性建筑——九层楼.某数学兴趣小组想利用所学的知识测量莫高窟九层楼的高度,并画出示意图如图②所示.具体方法如下:在地面C处测得楼顶A的仰角为60°,此时无人机从地面C处垂直上升到点D处,测得楼顶A的仰角为53.5°,且 . 已知点A,B,C,D在同一平面内,求莫高窟九层楼的高度AB.(结果保留整数,参考数据: , , , )
(1)、用直尺和圆规作∠BDC的平分线DE,交BC于点E(不写作法,保留作图痕迹);(2)、在(1)的条件下,判断DE与AC的位置关系,并写出证明过程.22. 敦煌莫高窟是中国现存规模最大、保存最为完好的佛教艺术宝库,被誉为“沙漠中的古代艺术画廊”,位于石窟群中段的红色楼阁(如图①),便是莫高窟标志性建筑——九层楼.某数学兴趣小组想利用所学的知识测量莫高窟九层楼的高度,并画出示意图如图②所示.具体方法如下:在地面C处测得楼顶A的仰角为60°,此时无人机从地面C处垂直上升到点D处,测得楼顶A的仰角为53.5°,且 . 已知点A,B,C,D在同一平面内,求莫高窟九层楼的高度AB.(结果保留整数,参考数据: , , , ) 23. 邮票素有“国家名片”之称,方寸之间,包罗万象.为宣传北京2022年冬奥会,中国邮政发行了若干套冬奥会纪念邮票,其中有一套展现雪上运动的邮票,如图所示:
23. 邮票素有“国家名片”之称,方寸之间,包罗万象.为宣传北京2022年冬奥会,中国邮政发行了若干套冬奥会纪念邮票,其中有一套展现雪上运动的邮票,如图所示:
某班级举行冬奥会有奖问答活动,答对的同学可以随机抽取邮票作为奖品.
(1)、在抢答环节中,若答对一题,可从4枚邮票中任意抽取1枚作为奖品,则恰好抽到“冬季两项”的概率是 .(2)、在抢答环节中,若答对两题,可从4枚邮票中任意抽取2枚作为奖品,请用列表或画树状图的方法,求恰好抽到“高山滑雪”和“自由式滑雪”的概率.24. 世界卫生组织预计:到2025年,全世界将会有一半人面临用水危机.为了倡导“节约用水,从我做起”,某县政府决定对县直属机关500户家庭一年的月平均用水量进行调查,调查小组随机抽查了部分家庭的月平均用水量(单位:吨),并将调查结果绘制成如图所示的条形统计图和扇形统计图.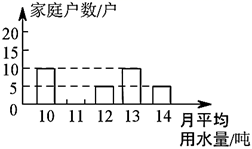

根据以上提供的信息,解答下列问题:
(1)、将条形统计图补充完整;(2)、求被调查家庭的月平均用水量的中位数吨、众数吨;(3)、估计该县直属机关 户家庭的月平均用水量不少于 吨的约有多少户?25. 心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分)的变化规律如图12所示(其中AB,BC分别为线段,CD为双曲线的一部分): (1)、开始上课后第5分钟与第30分钟相比较,何时学生的注意力更集中?(2)、一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题?26. 如图, 是 的直径,点C是 上异于A、B的点,连接 、 ,点D在 的延长线上,且 ,点E在 的延长线上,且 .
(1)、开始上课后第5分钟与第30分钟相比较,何时学生的注意力更集中?(2)、一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题?26. 如图, 是 的直径,点C是 上异于A、B的点,连接 、 ,点D在 的延长线上,且 ,点E在 的延长线上,且 .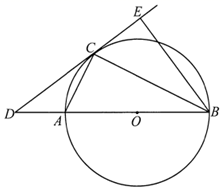 (1)、求证: 是 的切线:(2)、若 ,求 的长.27. 已知:正方形 中, , 绕点A顺时针旋转,它的两边分别交 (或它们的延长线)于点 .
(1)、求证: 是 的切线:(2)、若 ,求 的长.27. 已知:正方形 中, , 绕点A顺时针旋转,它的两边分别交 (或它们的延长线)于点 .当 绕点A旋转到 时(如图1),易证 .
 (1)、当 绕点A旋转到 时(如图2),线段 和 之间有怎样的数量关系?写出猜想,并加以证明.(2)、当 绕点A旋转到如图3的位置时,线段 和 之间又有怎样的数量关系?请直接写出你的猜想.28. 如图,抛物线y=ax2+bx+c与坐标轴交于点A(0,﹣3)、B(﹣1,0)、E(3,0),点P为抛物线上动点,设点P的横坐标为t.
(1)、当 绕点A旋转到 时(如图2),线段 和 之间有怎样的数量关系?写出猜想,并加以证明.(2)、当 绕点A旋转到如图3的位置时,线段 和 之间又有怎样的数量关系?请直接写出你的猜想.28. 如图,抛物线y=ax2+bx+c与坐标轴交于点A(0,﹣3)、B(﹣1,0)、E(3,0),点P为抛物线上动点,设点P的横坐标为t. (1)、若点C与点A关于抛物线的对称轴对称,求C点的坐标及抛物线的解析式;(2)、若点P在第四象限,连接PA、PE及AE,当t为何值时,△PAE的面积最大?最大面积是多少?(3)、是否存在点P,使△PAE为以AE为直角边的直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.
(1)、若点C与点A关于抛物线的对称轴对称,求C点的坐标及抛物线的解析式;(2)、若点P在第四象限,连接PA、PE及AE,当t为何值时,△PAE的面积最大?最大面积是多少?(3)、是否存在点P,使△PAE为以AE为直角边的直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.