北京市石景山区2022年中考一模数学试题
试卷更新日期:2022-07-06 类型:中考模拟
一、单选题
-
1. 在△ABC中, , , , a的值可能是( )A、1 B、3 C、5 D、72. 如图是某个几何体的展开图,该几何体是( )
 A、长方体 B、正方体 C、三棱柱 D、圆柱3. 实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A、长方体 B、正方体 C、三棱柱 D、圆柱3. 实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )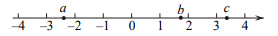 A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,△ABC中, , D,E分别为CB,AB上的点, , , 若 , 则DE的长为( )
A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,△ABC中, , D,E分别为CB,AB上的点, , , 若 , 则DE的长为( ) A、 B、2 C、 D、16. 方程组的解为( )A、 B、 C、 D、7. 研究与试验发展(R&D)经费是指报告期为实施研究与试验发展(R&D)活动而实际发生的全部经费支出.基础研究活动是研究与试验发展(R&D)活动的重要组成.下面的统计图是自2016年以来全国基础研究经费及占R&D经费比重情况.
A、 B、2 C、 D、16. 方程组的解为( )A、 B、 C、 D、7. 研究与试验发展(R&D)经费是指报告期为实施研究与试验发展(R&D)活动而实际发生的全部经费支出.基础研究活动是研究与试验发展(R&D)活动的重要组成.下面的统计图是自2016年以来全国基础研究经费及占R&D经费比重情况.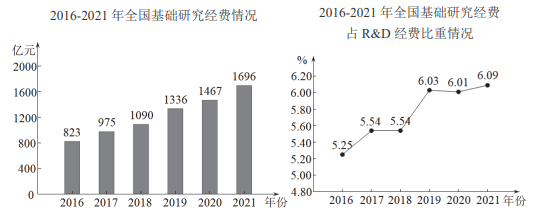
根据统计图提供的信息,下面四个推断中错误的是( )
A、2016年至2021年,全国基础研究经费逐年上升 B、2016年至2021年,全国基础研究经费占R&D经费比重逐年上升 C、2016年至2021年,全国基础研究经费平均值超过1000亿元 D、2021年全国基础研究经费比2016年的2倍还多8. 已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:…
﹣1
0
1
3
…
…
0
﹣1.5
﹣2
0
…
根据表格中的信息,得到了如下的结论:
①二次函数y=ax2+bx+c可改写为y=a(x−1) 2−2的形式
②二次函数y=ax2+bx+c的图象开口向下
③关于x的一元二次方程ax2+bx+c=−1.5的两个根为0或2
④若y>0,则x>3
其中所有正确的结论为( )
A、①④ B、②③ C、②④ D、①③二、填空题
-
9. 若代数式 有意义,则实数x的取值范围是 .10. 分式方程的解为 .11. 如图,将沿BC方向平移一定的距离得到 . 请写出一条正确的结论,可以为 .
 12. 在平面直角坐标系xOy中,点 , 都在反比例函数的图象上,则的值为 .13. , , 若 , , 请借助下图直观分析,通过计算求得的值为 .
12. 在平面直角坐标系xOy中,点 , 都在反比例函数的图象上,则的值为 .13. , , 若 , , 请借助下图直观分析,通过计算求得的值为 . 14. 如图,AB为⊙O的直径,点P在AB的延长线上,PC,PD分别与⊙O相切于点C,D,若∠CPA=40°,则∠CAD的度数为°.
14. 如图,AB为⊙O的直径,点P在AB的延长线上,PC,PD分别与⊙O相切于点C,D,若∠CPA=40°,则∠CAD的度数为°.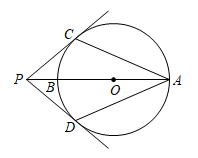 15. 某班级学生分组做抛掷瓶盖的试验,各组试验结果如下表:
15. 某班级学生分组做抛掷瓶盖的试验,各组试验结果如下表:累计抛掷次数
100
200
300
400
500
600
盖面朝上次数
54
105
158
212
264
319
盖面朝上的频率
0.5400
0.5250
0.5267
0.5300
0.5280
0.5317
根据表格中的信息,估计抛掷一枚这样的瓶盖,落地后盖面朝上的概率为 . (精确到0.01)
16. 如图,某建筑公司有A(1,3),B(3,3),C(5,3)三个建筑工地,三个工地的水泥日用量分别为a吨,b吨,c吨.有M(1,5),N(3,1)两个原料库供应水泥.使用一辆载重量大于(a+b+c)吨的运输车可沿图中虚线所示的道路运送水泥.为节约运输成本,公司要进行运输路线规划,使总的“吨千米数”(吨数×运输路程千米数)最小.若公司安排一辆装有(a+c)吨的运输车向A和C工地运送当日所需的水泥,且a>c,为使总的“吨千米数”最小,则应从原料库(填“M”或“N”)装运;若公司计划从N原料库安排一辆装有(a+b+c)吨的运输车向A,B,C三个工地运送当日所需的水泥,且a:b:c=3:2:1,为使总的“吨千米数”最小,写出向三个工地运送水泥的顺序(按运送的先后顺序依次排列即可).
三、解答题
-
17. 计算: .18. 解不等式组:并写出它的最大整数解.19. 已知 , 求代数式的值.20. 已知:如图,Rt△ABC中,∠ACB=90°,CB<CA.

求作:线段AB上的一点M,使得∠MCB=∠A.
作法:①以点C为圆心,CB长为半径作弧,交AB于点D;
②分别以点B,D为圆心,大于BD长为半径作弧,两弧在AB的右侧相交于点E;
③作直线CE,交AB于点M.∠MCB即为所求.
根据小伟设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接CD,ED,EB.
∵CD=CB,ED=EB,
∴CE是DB的垂直平分线( )(填推理的依据).
∴CM⊥AB.
∴∠MCB+∠B=90°.
∵∠ACB=90°,
∴∠A+∠B=90°.
∴∠MCB=∠A( )(填推理的依据).
21. 已知:关于x的一元二次方程 .(1)、求证:不论m取何值,方程总有两个不相等的实数根;(2)、选择一个你喜欢的整数m的值代入原方程,并求出这个方程的解.22. 如图所示,△ABC中,∠ACB=90°,D,E分别为AB,BC的中点,连接DE并延长到点F,使得EF=DE,连接CD,CF,BF.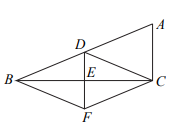 (1)、求证:四边形BFCD是菱形;(2)、若cosA= , DE=5,求菱形BFCD的面积.23. 在平面直角坐标系xOy中,直线与直线交于点 .(1)、当时,求n,b的值;(2)、过动点且垂直于x轴的直线与 , 的交点分别是C,D.当时,点C位于点D上方,直接写出b的取值范围.24. 如图,AB为⊙O的直径,C,D为⊙O上两点,= , 连接AC,BC,AD,BD,过点D作DE//AB交CB的延长线于点E.
(1)、求证:四边形BFCD是菱形;(2)、若cosA= , DE=5,求菱形BFCD的面积.23. 在平面直角坐标系xOy中,直线与直线交于点 .(1)、当时,求n,b的值;(2)、过动点且垂直于x轴的直线与 , 的交点分别是C,D.当时,点C位于点D上方,直接写出b的取值范围.24. 如图,AB为⊙O的直径,C,D为⊙O上两点,= , 连接AC,BC,AD,BD,过点D作DE//AB交CB的延长线于点E. (1)、求证:直线DE是⊙O的切线;(2)、若AB=10,BC=6,求AD,BE的长.25. 2022年是中国共产主义青年团成立100周年,某中学为普及共青团知识,举行了一次知识竞赛(百分制).为了解七、八年级学生的答题情况,从中各随机抽取了20名学生的成绩,并对数据(成绩)进行了整理、描述和分析.下面给出部分信息.
(1)、求证:直线DE是⊙O的切线;(2)、若AB=10,BC=6,求AD,BE的长.25. 2022年是中国共产主义青年团成立100周年,某中学为普及共青团知识,举行了一次知识竞赛(百分制).为了解七、八年级学生的答题情况,从中各随机抽取了20名学生的成绩,并对数据(成绩)进行了整理、描述和分析.下面给出部分信息.a.七年级学生竞赛成绩的频数分布表及八年级学生竞赛成绩的扇形统计图:
分组/分数
频数
频率
50≤x<60
1
0.05
60≤x<70
2
0.10
70≤x<80
5
0.25
80≤x<90
7
m
90≤x<100
5
0.25
合计
20
1

b.七年级学生竞赛成绩数据在这一组的是:
80 80 82 85 85 85 89
c.七、八两年级竞赛成绩数据的平均数、中位数、众数以及方差如下:
年级
平均数
中位数
众数
方差
七年级
82.0
n
85
109.9
八年级
82.4
84
85
72.1
根据以上信息,回答下列问题:
(1)、写出表中m,n的值:m= , n=;八年级学生竞赛成绩扇形统计图中,表示这组数据的扇形圆心角的度数是°;(2)、在此次竞赛中,竞赛成绩更好的是(填“七”或“八”)年级,理由为;(3)、竞赛成绩90分及以上记为优秀,该校七、八年级各有200名学生,估计这两个年级成绩优秀的学生共约人.26. 在平面直角坐标xOy中,点在抛物线上.(1)、求抛物线的对称轴;(2)、抛物线上两点 , , 且 , .①当时,比较 , 的大小关系,并说明理由;
②若对于 , , 都有 , 直接写出t的取值范围.
27. 如图,△ACB中, , , D为边BC上一点(不与点C重合), , 点E在AD的延长线上,且 , 连接BE,过点B作BE的垂线,交边AC于点F. (1)、依题意补全图形;(2)、求证:;(3)、用等式表示线段AF与CD的数量关系,并证明.28. 在平面直角坐标系xOy中,点P不在坐标轴上,点P关于x轴的对称点为P1 , 点P关于y轴的对称点为P2 , 称△P1PP2为点P的“关联三角形”.
(1)、依题意补全图形;(2)、求证:;(3)、用等式表示线段AF与CD的数量关系,并证明.28. 在平面直角坐标系xOy中,点P不在坐标轴上,点P关于x轴的对称点为P1 , 点P关于y轴的对称点为P2 , 称△P1PP2为点P的“关联三角形”. (1)、已知点A(1,2),求点A的“关联三角形”的面积;(2)、如图,已知点B(m,n),⊙T的圆心为T(2,2),半径为2.若点B的“关联三角形”与⊙T有公共点,直接写出m的取值范围;(3)、已知⊙O的半径为r,OP=2r,若点P的“关联三角形”与⊙O有四个公共点,直接写出∠PP1P2的取值范围.
(1)、已知点A(1,2),求点A的“关联三角形”的面积;(2)、如图,已知点B(m,n),⊙T的圆心为T(2,2),半径为2.若点B的“关联三角形”与⊙T有公共点,直接写出m的取值范围;(3)、已知⊙O的半径为r,OP=2r,若点P的“关联三角形”与⊙O有四个公共点,直接写出∠PP1P2的取值范围.