北京市丰台区2022年九年级一模数学试题
试卷更新日期：2022-07-06 类型：中考模拟
一、单选题
-
1. 如图是某几何体的三视图，该几何体是（ ）
A、长方体 B、三棱柱 C、圆柱 D、圆锥2. 根据国家统计局统计结果，从北京冬奥会申办成功至2021年10月，全国参与冰雪运动的人数达到3.46亿，“带动三亿人参与冰雪运动”的承诺已经实现，这是北京冬奥会最大的遗产成果．将346000000用科学记数法表示应为（ ）A、346×106 B、3.46×108 C、3.46×109 D、0.346×1093. 如图，直角三角板的直角顶点A在直线l上，如果∠1＝35°，那么∠2的度数是（ ）
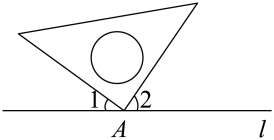A、55° B、45° C、35° D、25°4. 下列图形中，既是中心对称图形又是轴对称图形的是（ ）A、
B、
C、
D、
5. 实数a，b在数轴上的对应点的位置如图所示，下列结论中正确的是（ ）
A、a+b＜0 B、a﹣b＞0 C、ab＞0 D、|b|＞26. 不透明的袋子中有3个小球，其中有1个红球，1个黄球，1个绿球，除颜色外3个小球无其他差别，从中随机摸出一个小球，放回并摇匀，再从中随机摸出一个小球，那么两次摸出的小球都是红球的概率是（ ）A、 B、 C、 D、7. 如果3x﹣2y＝0，那么代数式（+1）•的值为（ ）A、1 B、2 C、3 D、48. 如图，长方体的体积是100m3 ， 底面一边长为2m．记底面另一边长为xm，底面的周长为lm，长方体的高为hm．当x在一定范围内变化时，l和h都随x的变化而变化，则l与x，h与x满足的函数关系分别是（ ）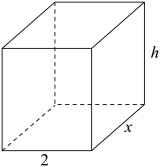
A、一次函数关系，二次函数关系 B、反比例函数关系，二次函数关系 C、反比例函数关系，一次函数关系 D、一次函数关系，反比例函数关系二、填空题
-
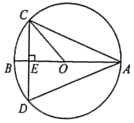
9. 若分式 有意义，则实数x的取值范围是 ．10. 分解因式：2x2﹣8=11. 写出一个比3大且比5小的无理数 ．12. 在平面直角坐标系xOy中，直线y＝x与双曲线y＝交于点A（2，m），则k的值是 ．13. 如图，⊙O的直径AB垂直于弦CD，垂足为E，∠CAD＝45°，则∠BOC＝°．
14. 如图，点B，E，C，F在一条直线上，BC＝EF，∠B＝∠DEF．只需添加一个条件即可证明△ABC≌△DEF，这个条件可以是 （写出一个即可）．
15. 如图是甲、乙两名射击运动员10次射击训练成绩的统计图，如果甲、乙这10次射击成绩的方差为s甲2 ， s乙2 ， 那么s甲2s乙2 ． （填“＞”，“＝”或“＜”）
16. 某工厂有甲、乙、丙、丁、戊五台车床．若同时启动其中两台车床，加工10000个W型零件所需时间如表：车床编号
甲、乙
乙、丙
丙、丁
丁、戊
甲、戊
所需时间（h）
13
9
10
12
8
则加工W型零件最快的一台车床的编号是 ．
三、解答题
-
17. 计算：（）﹣1﹣2cos30°+|﹣|﹣（3.14﹣π）0 ．18. 解不等式组： ．19. 已知关于x的一元二次方程x2﹣（m+2）x+m+1＝0．(1)、求证：该方程总有两个实数根；(2)、若该方程的两个实数根互为相反数，求m的值．20. 《周髀算经》中记载了一种确定东南西北方向的方法．大意是：在平地上点A处立一根杆，记录日出时杆影子的长度AB，并以点A为圆心，以AB为半径画圆，记录同一天日落时杆影子的痕迹与此圆的交点C，那么直线CB表示的方向就是东西方向，∠BAC的角平分线所在的直线表示的方向就是南北方向．
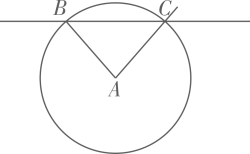(1)、上述方法中，点A，B，C的位置如图所示，使用直尺和圆规，在图中作∠BAC的角平分线AD（保留作图痕迹）；(2)、在图中，确定了直线CB表示的方向为东西方向，根据南北方向与东西方向互相垂直，可以判断直线AD表示的方向为南北方向，完成如下证明．证明：∵点B，C在⊙O上，
∴AB＝ ▲ ．
∴△ABC是等腰三角形．
∵AD平分∠BAC，
∴AD⊥BC （ ）（填推理的依据）．
∵直线CB表示的方向为东西方向，
∴直线AD表示的方向为南北方向．
21. 如图，在四边形ABCD中，∠DCB＝90°，ADBC，点E在BC上，ABDE，AE平分∠BAD．
(1)、求证：四边形ABED为菱形；(2)、连接BD，交AE于点O．若AE＝6，sin∠DBE＝ ， 求CD的长．22. 在平面直角坐标系xOy中，一次函数y＝kx+b（k≠0）的图象由函数y＝2x的图象平移得到，且经过点（2，1）．(1)、求这个一次函数的解析式；(2)、当x＞0时，对于x的每一个值，函数y＝mx（m≠0）的值大于一次函数y＝kx+b的值，直接写出m的取值范围．23. 如图，AB是⊙O的直径，C是⊙O上一点，连接AC．过点B作⊙O的切线，交AC的延长线于点D，在AD上取一点E，使AE＝AB，连接BE，交⊙O于点F，连接AF．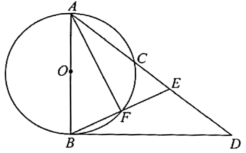
(1)、求证：∠BAF＝∠EBD；(2)、过点E作EG⊥BD于点G．如果AB＝5，BE＝2 ， 求EG，BD的长．24. 某公园在人工湖里安装一个喷泉，在湖心处竖直安装一根水管，在水管的顶端安一个喷水头，水柱从喷水头喷出到落于湖面的路径形状可以看作是抛物线的一部分．若记水柱上某一位置与水管的水平距离为d米，与湖面的垂直高度为h米．下面的表中记录了d与h的五组数据：d（米）
0
1
2
3
4
h（米）
0.5
1.25
1.5
1.25
0.5
根据上述信息，解决以下问题：
(1)、在下面网格（图1）中建立适当的平面直角坐标系，并根据表中所给数据画出表示h与d函数关系的图象；(2)、若水柱最高点距离湖面的高度为m米，则m=；(3)、现公园想通过喷泉设立新的游玩项目，准备通过只调节水管露出湖面的高度，使得游船能从水柱下方通过．如图2所示，为避免游船被喷泉淋到，要求游船从水柱下方中间通过时，顶棚上任意一点到水柱的竖直距离均不小于0.5米．已知游船顶棚宽度为3米，顶棚到湖面的高度为2米，那么公园应将水管露出湖面的高度（喷水头忽略不计）至少调节到多少米才能符合要求？请通过计算说明理由（结果保留一位小数）．25. 为了解地铁14号线与7号线的日客运强度，获得了它们2022年1月份工作日（共21天）日客运强度（单位：万人/公里）的数据，并对数据进行整理、描述和分析．下面给出了部分信息：
a．地铁14号线2022年1月份工作日日客运强度的数据的频数分布直方图如下（数据分成6组：0.50≤x＜0.70，0.70≤x＜0.90，0.90≤x＜1.10，1.10≤x＜1.30，1.30≤x＜1.50，1.50≤x≤1.70）；
b．地铁14号线2022年1月份工作日日客运强度的数据在1.30≤x＜1.50这一组是：
1.37 1.37 1.37 1.38 1.41 1.47 1.48 1.48 1.49c．地铁14号线与7号线2022年1月份工作日日客运强度的平均数、中位数如下：
平均数
中位数
地铁14号线
1.37
m
地铁7号线
1.08
1.1
根据以上信息，回答下列问题：
(1)、写出表中m的值；(2)、日客运强度反映了地铁的拥挤程度，小明每天上班均需乘坐地铁，可以选择乘坐地铁14号线或乘坐地铁7号线．请帮助小明选择一种乘坐地铁的方式，并说明理由；(3)、2022年一共有249个工作日，请估计2022年全年的工作日中，地铁14号线日客运强度不低于1.3万人/公里的天数（直接写出结果）．26. 在平面直角坐标系xOy中，点M（2，m），N（4，n）在抛物线y＝ax2+bx（a＞0）上．(1)、若m＝n，求该抛物线的对称轴；(2)、已知点P（﹣1，P）在该抛物线上，设该抛物线的对称轴为x＝t．若mn＜0，且m＜p＜n，求t的取值范围．27. 如图，在△ABC中，AB＝AC，∠BAC＝α，点D在边BC上（不与点B，C重合），连接AD，以点A为中心，将线段AD逆时针旋转180°﹣α得到线段AE，连接BE．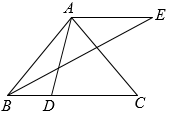
(1)、∠BAC+∠DAE＝°；(2)、取CD中点F，连接AF，用等式表示线段AF与BE的数量关系，并证明．28. 在平面直角坐标系xOy中，⊙O的半径为1，T（0，t）为y轴上一点，P为平面上一点．给出如下定义：若在⊙O上存在一点Q，使得△TQP是等腰直角三角形，且∠TQP＝90°，则称点P为⊙O的“等直点”，△TQP为⊙O的“等直三角形”．如图，点A，B，C，D的横、纵坐标都是整数．
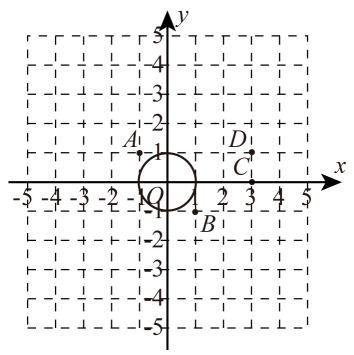(1)、当t＝2时，在点A，B，C，D中，⊙O的“等直点”是；(2)、当t＝3时，若△TQP是⊙O“等直三角形”，且点P，Q都在第一象限，求的值．