安徽省宣城市宣州区2022年九年级第二次模拟考试数学试题

试卷更新日期：2022-07-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列实数中，最小的是（）

A、 $- \sqrt{2}$ B、 $- \sqrt{5}$ C、0 D、3

查看试题解析
2. 计算 ${(- m^{2} n)}^{3}$ 的结果为（）

A、 $- m^{5} n^{3}$ B、 $m^{6} n^{3}$ C、 $- m^{6} n^{3}$ D、 $m^{5} n^{3}$

查看试题解析
3. 如图所示的几何体的主视图为（）

A、 B、 C、 D、

查看试题解析
4. 从省林业局获悉，我省实施“金银森林”行动，推动林业产业集聚发展，去年全省林业总产值达到5092亿元，保持在全国第一方阵，数据5092亿用科学记数法表示为（）

A、 $5.092 \times 1 0^{3}$ B、 $5.092 \times 1 0^{11}$ C、 $5.092 \times 1 0^{12}$ D、 $50.92 \times 1 0^{10}$

查看试题解析
5. 直线BD∥EF，两个直角三角板如图摆放，若∠CBD＝10°，则∠1＝（）

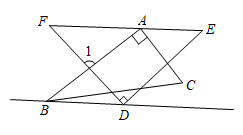A、75° B、80° C、85° D、95°

查看试题解析
6. 如图所示的电路中，随机闭合开关S₁ ， S₂ ， S₃中的两个，则能让两盏灯泡同时发光的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{1}{6}$ D、 $\frac{1}{3}$

查看试题解析
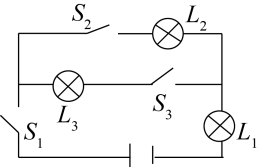7. 一次函数 $y = k x + b (k \neq 0)$ 的图象经过点 $A (- 2 ， m)$ ， $B (- 3 ， n)$ ，不经过第一象限，则下列关系正确的是（）

A、m＜n B、 $m > n$ C、m＝n D、不能确定

查看试题解析
8. 如图，在网格中小正方形的边长均为1，△ABC的顶点都在格点上，则 $s i n ∠ A B C$ 等于（）

A、 $\frac{1}{2}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{\sqrt{10}}{2}$

查看试题解析
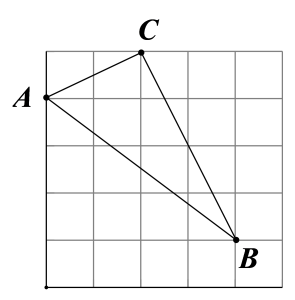9. 如图所示的是一圆弧形拱门，其中路面AB＝2m，拱高CD＝3m，则该拱门的半径为（）

A、 $\frac{5}{3} m$ B、2m C、 $\frac{8}{3} m$ D、3m

查看试题解析
10. 如图，P是矩形ABCD的一边BA延长线上一点，M是AD上一动点，连接PM与矩形ABCD的边交于点N，连接BM，BN，若AB＝6，AD＝2AP＝4，△BMN的面积为S，设DM＝x，则下列图象能反映S与x之间函数关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 计算 $\sqrt{8} + \sqrt{\frac{1}{2}}$ 的结果是．

查看试题解析
12. 分解因式： $2 m n^{2} - 50 m =$ ．

查看试题解析
13. 如图，菱形AOBC的顶点A在反比例函数 $y = \frac{3}{x}$ 的图象上，反比例函数 $y = \frac{k}{x}$ 的图象经过点C，若∠AOB＝60°，则k＝．

查看试题解析
14. 将二次函数 $y = - x^{2} - 4 x + 1$ 的图象先向右平移a个单位再向下平移2a个单位．

(1)、若平移后的二次函数图象经过点 $(1 ， - 1)$ ，则a＝．

(2)、平移后的二次函数图象与y轴交点的纵坐标最大值为．

查看试题解析

三、解答题

15. 解不等式组 ${\begin{array}{l} \frac{2 x - 1}{2} > 1 \\ \frac{2 - x}{3} > - \frac{1}{3} \end{array}$ ．

查看试题解析
16. △OAB在平面直角坐标系中的位置如图所示．

( 1 )画出与△OAB关于x轴对称的 $△ O A_{1} B_{1}$ ．（其中 $A_{1}$ 与A对称， $B_{1}$ 与B对称）

( 2 )将△OAB绕着点O顺时针方向旋转90°得到 $△ O A_{2} B_{2}$ ，画出 $△ O A_{2} B_{2}$ ．

查看试题解析
17. 为了节能减排，越来越多的市民使用共享电动车，图1为电动车实物图，图2为电动车示意图，AB与地面平行，已知车轮半径为15cm，BE＝40cm，∠ABE＝60°，若坐垫厚度为EM＝12cm，求坐垫M离地面的高度．（结果精确到1cm）（参考数据： $\sqrt{3} \approx 1.732$ ）

查看试题解析
18. 观察下列各式：
第1个等式： $\frac{2}{1 \times 3} = 1 - \frac{1}{3}$ ．
第2个等式： $\frac{2}{2 \times 4} = \frac{1}{2} - \frac{1}{4}$ ．
第3个等式： $\frac{2}{3 \times 5} = \frac{1}{3} - \frac{1}{5}$ ．
……
根据你发现的规律解答下列问题：

(1)、第4个等式为：．

(2)、写出你猜想的第n个等式：（用含n的等式表示），并证明．

查看试题解析
19. 如图，直线 $y_{1} = m x$ 与双曲线 $y_{2} = \frac{k}{x}$ 交于点A、B，过点A作AP⊥x轴，垂足P点的坐标是 $(- 2 ， 0)$ ，连接BP，且 $S_{△ A B P} = 4$ ．

(1)、求正比例函数 $y_{1} = m x$ 和反比例函数 $y_{2} = \frac{k}{x}$ 的解析式．

(2)、当 $y_{1} < y_{2}$ 时，求x的取值范围．

查看试题解析
20. 如图．AB是⊙O的直径，点C，D在⊙O上，C是 $\overset{⌢}{B D}$ 的中点，连接BD交AC于点E，延长AC至F，使CE＝CF．

(1)、求证：BF是⊙O的切线．

(2)、若BF＝3， $s i n A = \frac{1}{3}$ ，求BD的长．

查看试题解析
21. 2022年初由于新冠疫情，安徽部分市区学校响应“停课不停学”号召，积极实施线上教学，为了解线上教学情况，某校制定了网课效果调查表发至家长群中，其中用A表示“网课效果非常好”，B表示“网课效果比较好”，C表示“网课效果比较差”，D表示“网课效果非常差”，随机抽取了部分调查表，如图是老师根据调查表统计资料绘制的两幅不完整的统计图，请你根据统计图提供的信息解答以下问题：

(1)、计算图1中 $α$ 的度数，并通过计算补全条形统计图．

(2)、如果该校有2000名同学，请你估计该校“网课效果比较差”的同学有多少人？

(3)、其中被抽查的“网课效果非常好”的学生中有4人位于同一班级，分别为两男两女，现老师从这4人中抽出2名同学作经验分享以提高学生的网课效果，请用列表法或画树状图法求被抽到一男一女的概率．

查看试题解析
22. 如图，抛物线 $y = a x^{2} + b x + c$ 与x轴交于点A，B，与y轴交于点C，一次函数y＝－x＋3的图象经过点B，C，与抛物线对称轴交于点D，且 $S_{△ A B D} = 4$ ，点P是抛物线 $y = a x^{2} + b x + c$ 上的动点．

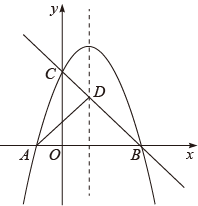(1)、求抛物线的函数解析式．

(2)、当点P在直线BC上方时，求点P到直线BC的距离的最大值．

查看试题解析
23. 某数学兴趣小组在数学课外活动中，对多边形内两条互相垂直的线段做了如下探究：

(1)、如图1，在正方形ABCD中，E，F分别是AB，AD上的两点，连接DE，CF，若DE⊥CF，求证：CF＝DE．

(2)、如图2，在矩形ABCD中，过点C作CE⊥BD交AD于点E，若 $t a n ∠ D C E = \frac{2}{3}$ ，求 $\frac{C E}{B D}$ 的值．

(3)、如图3，在四边形ABCD中，∠A＝∠B＝90°，E为AB上一点，连接DE，过点C作DE的垂线交ED的延长线于点G，交AD的延长线于点F，且AB＝5，AD＝3，CF＝7．求DE的长．

查看试题解析