云南省大理市2022年九年级中考第一次统一检测数学试题
试卷更新日期:2022-07-06 类型:中考模拟
一、单选题
-
1. 如果水库的水位高于正常水位2m时,记作+2m,那么低于正常水位3m时,应记作( ).A、+3m B、-3m C、+ m D、 m2. 如图,已知 ABCD,∠1=47°,则∠2 的度数是( )
 A、43° B、147° C、47° D、133°3. 下列运算正确的是( )A、 B、 C、 D、4. 下列用相同的正方体堆放在一起组成的几何体中,主视图和左视图不相同的是( )A、
A、43° B、147° C、47° D、133°3. 下列运算正确的是( )A、 B、 C、 D、4. 下列用相同的正方体堆放在一起组成的几何体中,主视图和左视图不相同的是( )A、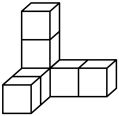 B、
B、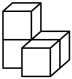 C、
C、 D、
D、 5. 已知正多边形的一个外角为36°,则该正多边形的边数为( )A、10 B、9 C、8 D、66. 随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递80件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件 件,根据题意可列方程为( )A、 B、 C、 D、7. 如图,已知 , CD和BE相交于点O, , 则AE∶EC为( )
5. 已知正多边形的一个外角为36°,则该正多边形的边数为( )A、10 B、9 C、8 D、66. 随着快递业务的增加,某快递公司为快递员更换了快捷的交通工具,公司投递快件的能力由每周3000件提高到4200件,平均每人每周比原来多投递80件,若快递公司的快递员人数不变,求原来平均每人每周投递快件多少件?设原来平均每人每周投递快件 件,根据题意可列方程为( )A、 B、 C、 D、7. 如图,已知 , CD和BE相交于点O, , 则AE∶EC为( ) A、3:5 B、9:25 C、3:2 D、5:38. 高尔基说:“书,是人类进步的阶梯”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )
A、3:5 B、9:25 C、3:2 D、5:38. 高尔基说:“书,是人类进步的阶梯”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )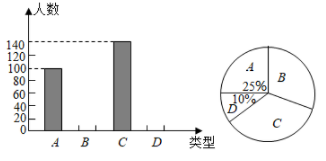 A、样本容量为400 B、类型D所对应的扇形的圆心角为 C、类型C所占百分比为 D、类型B的人数为120人9. 如图, 是 的外接圆, 交 于点E,垂足为点D, , 的延长线交于点F.若 , ,则 的长是( )
A、样本容量为400 B、类型D所对应的扇形的圆心角为 C、类型C所占百分比为 D、类型B的人数为120人9. 如图, 是 的外接圆, 交 于点E,垂足为点D, , 的延长线交于点F.若 , ,则 的长是( )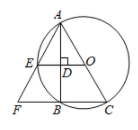 A、10 B、8 C、6 D、410. 计算3的正整数次幂: , , , , , , , …观察归纳各计算结果中个位数字的规律,可得的个位数字是( )A、1 B、3 C、7 D、911. 如图,点E在边长为4的正方形ABCD的CD边上,连接BE,将△BCE沿直线BE翻折,点C的对应点为C′,延长BC′交AD边于点F,若AF=3,则tan∠CBE的值为( )
A、10 B、8 C、6 D、410. 计算3的正整数次幂: , , , , , , , …观察归纳各计算结果中个位数字的规律,可得的个位数字是( )A、1 B、3 C、7 D、911. 如图,点E在边长为4的正方形ABCD的CD边上,连接BE,将△BCE沿直线BE翻折,点C的对应点为C′,延长BC′交AD边于点F,若AF=3,则tan∠CBE的值为( ) A、 B、 C、 D、212. 若关于x的不等式组有且只有4个整数解,且关于y的一元二次方程有两个不相等的实数根,则符合条件的所有整数m的和为( )A、26 B、24 C、21 D、15
A、 B、 C、 D、212. 若关于x的不等式组有且只有4个整数解,且关于y的一元二次方程有两个不相等的实数根,则符合条件的所有整数m的和为( )A、26 B、24 C、21 D、15二、填空题
-
13. 2021年5月15日7时18分,执行我国首次火星探测任务的“天问一号”探测器在火星着落,在火星上首次留下中国印迹.火星是太阳系九大行星之一,火星的半径约为3395000米,用科学记数法表示“3395000”为 .14. 分解因式: -25a =15. 使代数式有意义的x的取值范围是 .16. 如图,已知点A在反比例函数 的图象上,过点A作 轴于点B , 的面积是2.则k的值是 .
 17. 要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为 , 侧面积为 , 则这个扇形的圆心角的度数是 .18. 在平行四边形ABCD中,AB=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AD的长为 .
17. 要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为 , 侧面积为 , 则这个扇形的圆心角的度数是 .18. 在平行四边形ABCD中,AB=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AD的长为 .三、解答题
-
19. 某校德育处利用班会课对全校学生进行了一次防疫知识测试活动,现从初二、初三两个年级各随机抽取了15名学生的测试成绩,得分用x表示,共分成4组:A: , B: , C: , D: , 对得分进行整理分析,给出了下面部分信息:
初二的测试成绩在C组中的数据为:80,86,88.
初三的测试成绩:76,83,100,88,81,100,82,71,95,90,100,93,89,86,86.
年级
平均数
中位数
最高分
众数
初二
88
a
98
98
初三
88
88
100
b
 (1)、a= , b=;(2)、通过以上数据分析,你认为(填“初二”或“初三”)学生对防疫知识的掌握更好?请写出一条理由;(3)、若初二、初三共有1500名学生,请估计此次测试成绩达到90分及以上的学生约有多少人?20. 第二十四届冬奥会于2022年2月20日在北京闭幕,北京成为全球首个既举办过夏季奥运会义举办过冬季奥运会的城市.如图,是四张关于冬奥会运动项目的卡片,卡片的正面分别印有A.“花样滑冰”、B.“高山滑雪”、C.“单板滑雪大跳台”、D.“钢架雪车”(这四张卡片除正面图案外,其余都相同).将这四张卡片背面朝上,洗匀.
(1)、a= , b=;(2)、通过以上数据分析,你认为(填“初二”或“初三”)学生对防疫知识的掌握更好?请写出一条理由;(3)、若初二、初三共有1500名学生,请估计此次测试成绩达到90分及以上的学生约有多少人?20. 第二十四届冬奥会于2022年2月20日在北京闭幕,北京成为全球首个既举办过夏季奥运会义举办过冬季奥运会的城市.如图,是四张关于冬奥会运动项目的卡片,卡片的正面分别印有A.“花样滑冰”、B.“高山滑雪”、C.“单板滑雪大跳台”、D.“钢架雪车”(这四张卡片除正面图案外,其余都相同).将这四张卡片背面朝上,洗匀. (1)、从中随机抽取一张,求抽得的卡片恰好为“花样滑冰”的概率;(2)、若从中随机抽取两张卡片,请你用列表或画树状图的方法,求抽取的卡片中有“高山滑雪”的概率.21. 如图,四边形ABCD是平行四边形, , BE、DF分别交AC于点E,F.
(1)、从中随机抽取一张,求抽得的卡片恰好为“花样滑冰”的概率;(2)、若从中随机抽取两张卡片,请你用列表或画树状图的方法,求抽取的卡片中有“高山滑雪”的概率.21. 如图,四边形ABCD是平行四边形, , BE、DF分别交AC于点E,F. (1)、求证:;(2)、当四边形ABCD是菱形时,请判断四边形BEDF的形状,并证明你的结论.22. 农技人员对培育的某一品种桃树进行研究,发现桃子成熟后一棵树上每个桃子质量大致相同.以每棵树上桃子的数量x(个)为横坐标、桃子的平均质量y(克/个)为纵坐标,在平面直角坐标系中描出对应的点,发现这些点大致分布在直线AB附近(如图所示).
(1)、求证:;(2)、当四边形ABCD是菱形时,请判断四边形BEDF的形状,并证明你的结论.22. 农技人员对培育的某一品种桃树进行研究,发现桃子成熟后一棵树上每个桃子质量大致相同.以每棵树上桃子的数量x(个)为横坐标、桃子的平均质量y(克/个)为纵坐标,在平面直角坐标系中描出对应的点,发现这些点大致分布在直线AB附近(如图所示).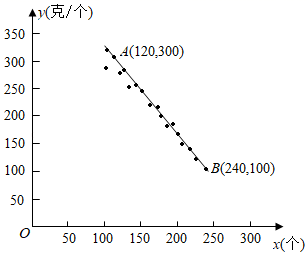 (1)、求直线AB的函数关系式;(2)、市场调研发现:这个品种每个桃子的平均价格w(元)与平均质量y(克/个)满足函数表达式w= y+2.在(1)的情形下,求一棵树上桃子数量为多少时,该树上的桃子销售额最大?
(1)、求直线AB的函数关系式;(2)、市场调研发现:这个品种每个桃子的平均价格w(元)与平均质量y(克/个)满足函数表达式w= y+2.在(1)的情形下,求一棵树上桃子数量为多少时,该树上的桃子销售额最大?