（人教版）2022年暑假复习巩固专题2垂线

试卷更新日期：2022-07-06 类型：复习试卷

进入出卷网下载

一、单选题

1. 点P为直线 $M N$ 外一点，点A、B、C为直线 $M N$ 上三点， $P A = 4 c m$ ， $P B = 5 c m$ ， $P C = 2 c m$ ，则P到直线 $M N$ 的距离为（）

A、 $4 c m$ B、 $2 c m$ C、小于 $2 c m$ D、不大于 $2 c m$

查看试题解析
2. 若点P为直线l外一点，点A、B、C为直线l上的不同的点，其中 $P A = 4$ ， $P B = 5$ ， $P C = 6$ ，那么点P到直线l的距离是（）

A、小于4 B、4 C、小于或等于4 D、大于或等于4

查看试题解析
3. 如图，OB⊥OD，OC⊥OA，∠BOC＝32°，那么∠AOD等于（）

A、148° B、132° C、128° D、90°

查看试题解析
4. 如图，已知AC⊥BC，CD⊥AB，垂足分别是C，D，其中AC＝6，BC＝8，AB＝10，CD＝4.8，那么点B到AC的距离是（）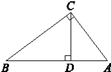

A、6 B、8 C、10 D、4.8

查看试题解析
5. 如图，点A、C、B在同一直线上，DC⊥EC，若∠BCD＝40°，则∠ACE的度数是（）

A、30° B、40° C、50° D、60°

查看试题解析
6. 点P为直线m外一点，点A、B、C是直线m上三点， $P A = 4 c m$ ， $P B = 4 c m$ ， $P C = 2 c m$ ，则点P到直线m的距离为（）

A、4cm B、5cm C、2cm D、小于或等于2cm

查看试题解析
7. 如图，AB⊥CD，垂足为O，EF为过点O的一条直线，若∠1＝50°，则∠2的度数为（）

A、30° B、40° C、45° D、50°

查看试题解析
8. 如图所示，在灌溉农田时，要把河（直线 $l$ 表示一条河）中的水引到农田 $P$ 处，设计了四条路线 $P A 、 P B 、 P C 、 P D$ ，你选择哪条路线挖渠才能使渠道最短（）

A、 $P A$ B、 $P B$ C、 $P C$ D、 $P D$

查看试题解析
9. 如图所示，P是直线l外一点，点A，B，C在l上，且PB⊥l，垂足是B，下列说法：①PA，PB，PC这3条线段中，PB最短；②点P到直线l的距离是线段PB的长；③线段AB的长是点A到PB的距离；④线段PA的长是点P到直线l的距离．其中正确的是（）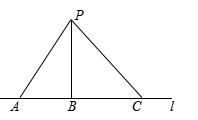

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
10. 如图，三角形 $A B C$ 中， $∠ B A C = 90 °$ ， $A D ⊥ B C$ ，垂足为 $D$ ，则下列结论正确的是（）

A、点 $C$ 到 $A B$ 的垂线段是线段 $A B$ B、 $A D > A C$ C、点 $A$ 到 $B C$ 的距离是线段 $A D$ 的长度 D、 $A D < B D$

查看试题解析

二、填空题

11. 如图是小凡同学在体育课上跳远后留下的脚印，他的跳远成绩是线段BN的长度，这样测量的依据是.

查看试题解析
12. 点O在直线AB上，过点O作射线OC、OD，使得 $O C ⊥ O D$ ，若 $∠ A O C = 30 °$ ，则 $∠ B O D$ 的度数是．

查看试题解析
13. 如图，直线 $A B ， C D$ 相交于O， $O E$ 平分 $∠ A O C ， O F ⊥ O E$ ，若 $∠ B O D = 46 °$ ，则 $∠ D O F$ 的度数为 $°$ ．

查看试题解析
14. 在平面直角坐标系中，点 $A$ 、 $B$ 的坐标为： $A (a ， 3)$ 、 $B (- 3 ， - 2)$ ，若线段 $A B$ 最短，则 $a$ 的值为．

查看试题解析
15. 如图，直线 AB，CD 相交于点 O，EO⊥AB，垂足为 O，∠BOC：∠COE=13：4，则∠AOC=.

查看试题解析

三、解答题

16. 如图，直线AB，CD相交于点O.射线OF⊥CD于点O，∠BOF=30°，求∠BOD，∠AOD的度数.

查看试题解析
17. 如图，已知直线 $A B$ 和 $C D$ 相交于O点，射线 $O E ⊥ A B$ 于O，射线 $O F ⊥ C D$ 于O，且 $∠ B O F = 20 °$ .求 $∠ E O D$ 的度数.

查看试题解析
18. 如图，直线AB、CD相交于点O，OE⊥CD，垂足为O，∠AOC＝35°，求∠BOE的度数.

查看试题解析
19. 如图，∠1=28°，AB⊥CD，垂足为O，EF经过点O.求∠2、∠3的度数.

查看试题解析
20. 如图，直线AB､CD相交于点O，EF⊥AB于O，且∠COE =50°，求∠BOD的度数

查看试题解析
21. 如图，已知直线 $A B$ ， $C D$ 相交于点O， $∠ A O D = 56 °$ ， $O E$ 平分 $∠ B O C$ ，且 $O F ⊥ O E$ ，求 $∠ C O F$ 的度数.

查看试题解析
22. 如图所示，直线 $A B$ ， $E F$ 交于点 $O$ ， $O D$ 平分 $∠ B O F$ ， $C O ⊥ E F$ 于点 $O$ ， $∠ A O E = 70 °$ ，求 $∠ C O D$ 的度数

查看试题解析
23. 如图，直线AB、CD相交于点O，EO⊥AB，垂足为O，∠EOC：∠AOD=7：11，求∠DOE的度数.

查看试题解析