2022-2023初数北师大版八年级上册1.2 一定是直角三角形吗 同步练习
试卷更新日期:2022-07-05 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 下列四组线段中,可以构成直角三角形的是( )A、4,5,6 B、2,3,4 C、3,4,5 D、1, , 32. 下列各组数据中,不能作为直角三角形边长的是( )A、3,5,7 B、6,8,10 C、5, 12, 13 D、1, , 23. 下列各组数中,以它们为边长的线段能构成直角三角形的是( )A、1,3,4 B、 C、5,12,13 D、4. 如图,五根小木棒,其长度分别为5,9,12,13,15,现将它们摆成两个直角三角形,其中正确的是( )A、
 B、
B、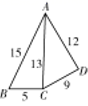 C、
C、 D、
D、 5. 有4条线段,分别为 , , , ,从中任取3条,能构成直角三角形的概率是( ).A、 B、 C、 D、6. 将一个直角三角形的三边长同时扩大10倍,得到的三角形是( )A、钝角三角形 B、锐角三角形 C、直角三角形 D、等腰三角形7. 如图,在四边形中, , , , , 且 , 则四边形的面积是( )
5. 有4条线段,分别为 , , , ,从中任取3条,能构成直角三角形的概率是( ).A、 B、 C、 D、6. 将一个直角三角形的三边长同时扩大10倍,得到的三角形是( )A、钝角三角形 B、锐角三角形 C、直角三角形 D、等腰三角形7. 如图,在四边形中, , , , , 且 , 则四边形的面积是( ) A、4 B、 C、 D、8. 如图,A,B,C是某社区的三栋楼,若在AC中点D处建一个5G基站,其覆盖半径为300 m,则这三栋楼中在该5G基站覆盖范围内的是( )
A、4 B、 C、 D、8. 如图,A,B,C是某社区的三栋楼,若在AC中点D处建一个5G基站,其覆盖半径为300 m,则这三栋楼中在该5G基站覆盖范围内的是( ) A、A,B,C都不在 B、只有B C、只有A,C D、A,B,C9. 在海面上有两个疑似漂浮目标. 接到消息后,A舰艇以12海里/时的速度离开港口O , 向北偏西50°方向航行. 同时,B舰艇在同地以16海里/时的速度向北偏东方向行驶,如图所示,离开港口1.5小时后两船相距30海里,则B舰艇的航行方向是( )
A、A,B,C都不在 B、只有B C、只有A,C D、A,B,C9. 在海面上有两个疑似漂浮目标. 接到消息后,A舰艇以12海里/时的速度离开港口O , 向北偏西50°方向航行. 同时,B舰艇在同地以16海里/时的速度向北偏东方向行驶,如图所示,离开港口1.5小时后两船相距30海里,则B舰艇的航行方向是( ) A、北偏东60° B、北偏东50° C、北偏东40° D、北偏东30°10. 如图,已知 中 , , ,在 上取一点E, 上取一点F,使得 ,过点C作 ,交 于点G,过点B作 .则 的度数为( )
A、北偏东60° B、北偏东50° C、北偏东40° D、北偏东30°10. 如图,已知 中 , , ,在 上取一点E, 上取一点F,使得 ,过点C作 ,交 于点G,过点B作 .则 的度数为( )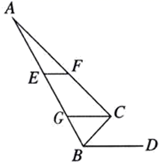 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 在△ABC中,若AC2+BC2=AB2 , ∠A∶∠B=1∶2,则∠B的度数是.12. 李老师要做一个直角三角形教具,做好后量得三边长分别是30 cm,40 cm和50 cm,则这个教具(填“ 合格”或“不合格”).13. 如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为.
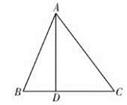 14. 如图所示,小明和组员想知道在水平地面上立的旗杆是否垂直于地面,已知旗杆高20米.从旗杆顶部拉下来一根绳子,测得绳子一端离旗杆底部BC长15.5 米,绳子长25米.那么旗杆是否与地面垂直?答案为:(填“是”或“不是”)
14. 如图所示,小明和组员想知道在水平地面上立的旗杆是否垂直于地面,已知旗杆高20米.从旗杆顶部拉下来一根绳子,测得绳子一端离旗杆底部BC长15.5 米,绳子长25米.那么旗杆是否与地面垂直?答案为:(填“是”或“不是”) 15. 如图,在单位为1的正方形网格中,有三条线段a,b,c(线段端点都在格点上),以这三条线段为边能否组成一个直角三角形?答: . (填“能”或“不能”.)
15. 如图,在单位为1的正方形网格中,有三条线段a,b,c(线段端点都在格点上),以这三条线段为边能否组成一个直角三角形?答: . (填“能”或“不能”.) 16. 如图,在△ABC中,AC=24,AB=25,BC=7.在AB上取一点E,AC上取一点F,连接EF,若∠EFC=125°,过点B作BD∥EF,且点D在AB的右侧,则∠CBD的度数为 .
16. 如图,在△ABC中,AC=24,AB=25,BC=7.在AB上取一点E,AC上取一点F,连接EF,若∠EFC=125°,过点B作BD∥EF,且点D在AB的右侧,则∠CBD的度数为 .
三、解答题(共8题,共52分)
-
17. 如图,正方形网格中,小格的顶点叫做格点,按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连接三个格点,使之构成直角三角形.小华在下边的正方形网格中作出了 .


 (1)、你认为小华作出的是直角三角形吗?请给予说明;(2)、请你按照同样的要求,在上边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等.18. 一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和地面是否垂直,为什么?
(1)、你认为小华作出的是直角三角形吗?请给予说明;(2)、请你按照同样的要求,在上边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等.18. 一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和地面是否垂直,为什么? 19. 如图所示的一块空地进行草坪绿化,已知 AD=4m ,CD=3m,AD⊥DC,AB=13m ,BC=12m ,绿化草坪价格 150 元/米2。求这块地草坪绿化的价钱.
19. 如图所示的一块空地进行草坪绿化,已知 AD=4m ,CD=3m,AD⊥DC,AB=13m ,BC=12m ,绿化草坪价格 150 元/米2。求这块地草坪绿化的价钱.
 20. 如图,四边形 中, , , , , ,求证: .
20. 如图,四边形 中, , , , , ,求证: . 21. 如图,在正方形网格中,每个小正方形的边长均是1,A,B,C为格点(每个小正方形的顶点叫格点).
21. 如图,在正方形网格中,每个小正方形的边长均是1,A,B,C为格点(每个小正方形的顶点叫格点). (1)、填空:线段 , , ;(2)、判断 的形状,并说明理由.22. 在 中, , , 的对边分别是a,b,c,根据下列各边的长度,判断各三角形是否为直角三角形.并指出哪一个角是直角.(1)、 , , ;(2)、 , , ;
(1)、填空:线段 , , ;(2)、判断 的形状,并说明理由.22. 在 中, , , 的对边分别是a,b,c,根据下列各边的长度,判断各三角形是否为直角三角形.并指出哪一个角是直角.(1)、 , , ;(2)、 , , ;

