2022-2023初数北师大版八年级上册1.1探索勾股定理 同步练习
试卷更新日期：2022-07-05 类型：同步测试
一、单选题（每题3分，共30分）
-
1. 若直角三角形的两边长分别是5和12，则它的斜边长是（ ）A、13 B、13或 C、 D、12或132. 如图，已知钓鱼竿 的长为 ，露在水面上的鱼线 长为 ，某钓鱼者想看看鱼钩上的情况，把鱼竿 转动到 的位置，此时露在水面上的鱼线 为 ，则 的长为（ ）
A、 B、 C、 D、3. 如图，在△ABC中，∠ACB=90°，点D是AB的中点，连接CD，若AC=4，BC=3，则CD的长度是（ )
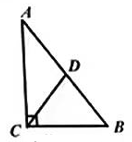A、1.5 B、2 C、2.5 D、54. 如图，在△ABC中，∠C＝90°，AC＝3 ，BC＝2．以AB为一条边向三角形外部作正方形，则正方形的面积是（ ）
A、5 B、6 C、12 D、135. 如图，在长方形ABCD中，分别按图中方式放入同样大小的直角三角形纸片．如果按图①方式摆放，刚好放下4个；如果按图②方式摆放，刚好放下3个．若BC＝4a，则按图③方式摆放时，剩余部分CF的长为（ ）
A、 B、 C、 D、6. 如图所示，在△ABC中，∠ACB＝90°，分别以AB、BC、AC为边向外作正方形，若三个正方形的面积分别为225、400、S，则S的值为（ ）
A、25 B、175 C、600 D、6257. 如图，RtΔABC中，AB=9，BC=6，∠B=90°，将ΔABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（ ）
A、 B、 C、4 D、58. 我国古代著名的“赵爽弦图”的示意图如图所示，它是由四个全等的直角三角形围成的．若AC＝2，BC＝3，将四个直角三角形中边长为3的直角边分别向外延长一倍，得到一个如图所示“数学风车”，则这个风车的外围周长是（ ）
A、 B、8 C、 D、9. 设a、b是直角三角形的两条直角边，若该三角形的周长为6，斜边长为2.5，则 的值是（ ）A、3 B、2.5 C、2 D、610. 如图1，分别以直角三角形三边为边向外作方形，面积分别为S1 ， S2 ， S3；如图2，分别以直角三角形三边长为直径向外作半圆，面积分别为S4 ， S5 ， S6 ， 其中S1＝1，S2＝3，S5＝2，S6＝4，则S3+S4＝（ ）
A、10 B、9 C、8 D、7二、填空题（每题3分，共18分）
-
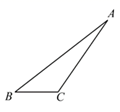
11. 设x>0，若以x+1，x+2，x+3为边长的三角形是直角三角形，则x的值为 ．12. 如图，在 ABC中，AB＝20，AC＝15，BC＝7，则点A到BC的距离是.
13. 如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”，在Rt△ABC中，∠C=90° ，AC=2，若Rt△ABC是“好玩三角形”，则AB= ．14. 如图，某斜拉桥的主梁AD垂直于桥面MN于点D，主梁上两根拉索AB、AC长分别为13米、20米，主梁AD的高度为12米，则固定点B、C之间的距离为米.
15. 如图是一机器人比赛行走的路径，机器人从A处先往东走8m ， 又往北走3m ， 遇到障碍后又往西走4m ， 再转向北走9m往东拐，仅走1m就到达了B ． 问A、B两点之间的距离为m ．
16. 一长方体容器（如图1），长，宽均为4，高为16，里面盛有水，水面高为10，若沿底面一棱进行旋转倾斜，倾斜后的长方体容器的主视图如图2所示，若倾斜容器使水恰好倒出容器，则 的长为 ．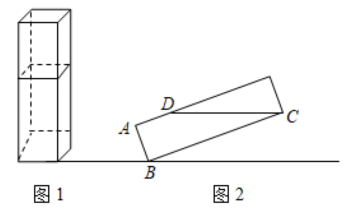
三、解答题（共8题，共52分）
-
17. 如图，△ABC中，∠ABC＝45°，F是高AD和高BE的交点，AC＝ ， BD＝2．求线段DF的长度．
18. 如图，甲乙两船从港口A同时出发，甲船以16海里/时速度向北偏东40°航行，乙船向南偏东50°航行，3小时后，甲船到达C岛，乙船到达B岛．若C、B两岛相距60海里，问乙船的航速是多少．
19. 已知△ABC中，AB＝AC，CD⊥AB于D，若AB＝5，CD＝3，求BC的长．
20. 已知，如图，在△ABC中，∠C＝ 90°，AD平分∠BAC交BC于D，过D作DE∥AC交AB于E．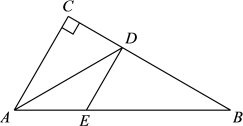
(1)、求证：AE＝DE；(2)、如果AC＝3， ， 求AE的长．21. 如图：已知ABCD，BC⊥CD，且CD＝2AB＝12，BC＝8，E是AD的中点.
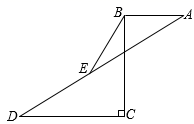(1)、请你用直尺（无刻度）作出一条线段与BE相等，并证明之；(2)、求BE的长.22. 如图直角三角形纸片中，∠C＝90°，AB＝10，BC＝8，AC＝6，沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD.
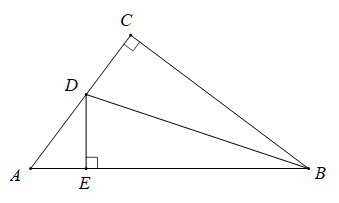(1)、求△ADE的周长；(2)、求DE的长.
