(人教版)2022-2023学年八年级数学入学综合测试卷(七)
试卷更新日期:2022-07-05 类型:复习试卷
一、单选题
-
1. 某中学七年级进行了一次数学测验,参加人数共400人,为了了解这次数学测验成绩,下列所抽取的样本中较为合理的是( )A、抽取前100名同学的数学成绩 B、抽取后100名同学的数学成绩 C、抽取其中100名女子的数学成绩 D、抽取各班学号为5的倍数的同学的数学成绩2. 在频数直方图中,共有7个小长方形,若中间一个小长方形的面积等于其他6个小长方形的面积的和的 , 且共有100个数据,则中间这一组数据的频数是( )A、25 B、20 C、0.25 D、0.23. 为了解某校初三年级学生的运算能力﹐抽取了100名学生进行测试,将所得成绩(单位:分)整理后,列出下表:
分组
50~59
60~69
70~79
80~89
90~99
频数
6
16
8
30
40
本次测试的这100名学生的成绩为良好的(大于或等于80分为良好)频率是( )
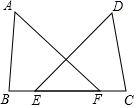
A、0.22 B、0.30 C、0.60 D、0.704. 空气是由多种气体混合而成的,为了直观地介绍空气各成分的百分比,最适合使用的统计图是( )A、条形图 B、扇形图 C、折线图 D、频数分布直方图5. 如图,△ABC中,D,E分别为BC,AD的中点,若△CDE的面积使2,则△ABC的面积是( )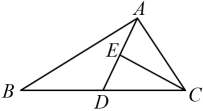 A、4 B、5 C、6 D、86. △ABC中,∠A=60°,∠B=80°,则∠C的度数为( )A、80° B、40° C、60° D、50°7. 一个多边形截去一个角后,得到的多边形的内角和为 ,那么原来的多边形的边数为( ).A、12或13取14 B、13或14 C、12或13 D、13或14或158. 如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,下列不正确的等式是( )
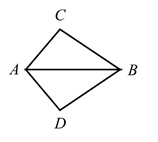
A、4 B、5 C、6 D、86. △ABC中,∠A=60°,∠B=80°,则∠C的度数为( )A、80° B、40° C、60° D、50°7. 一个多边形截去一个角后,得到的多边形的内角和为 ,那么原来的多边形的边数为( ).A、12或13取14 B、13或14 C、12或13 D、13或14或158. 如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,下列不正确的等式是( )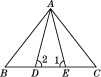 A、AD=DE B、∠BAE=∠CAD C、BE=DC D、AB=AC9. 如图是一个平分角的仪器,其中 , . 将点A放在一个角的顶点,AB和AD沿着这个角的两边放下,利用全等三角形的性质就能说明射线AC是这个角的平分线,这里判定ABC和ADC是全等三角形的依据是( )
A、AD=DE B、∠BAE=∠CAD C、BE=DC D、AB=AC9. 如图是一个平分角的仪器,其中 , . 将点A放在一个角的顶点,AB和AD沿着这个角的两边放下,利用全等三角形的性质就能说明射线AC是这个角的平分线,这里判定ABC和ADC是全等三角形的依据是( )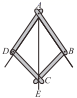 A、SSS B、ASA C、SAS D、AAS10. 已知:在 中, , 平分 交BC于D,若 ,且 ,则点D到AB边的距离为( )A、18 B、12 C、14 D、16
A、SSS B、ASA C、SAS D、AAS10. 已知:在 中, , 平分 交BC于D,若 ,且 ,则点D到AB边的距离为( )A、18 B、12 C、14 D、16二、填空题
-
11. 如图,整个圆表示某班参加课外活动的总人数,跳绳的人数占30%,表示踢毽的扇形圆心角是60°,踢毽和打篮球的人数比是12,那么表示参加“其它”活动的人数占总人数的%.
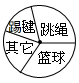 12. 已知某组数据的频率是0.25,样本容量是500,则这组数据的频数是 .13. 若三角形的两条边的长分别为4和5,第三边的长为x,则x 的取值范围是.14. 从n边形一个顶点可引9条对角线,则n= .15. 如图,在ABC中, ∠A=90°,BD平分∠ABC,交AC于点D,已知AD=4,则D到BC边的距离为.
12. 已知某组数据的频率是0.25,样本容量是500,则这组数据的频数是 .13. 若三角形的两条边的长分别为4和5,第三边的长为x,则x 的取值范围是.14. 从n边形一个顶点可引9条对角线,则n= .15. 如图,在ABC中, ∠A=90°,BD平分∠ABC,交AC于点D,已知AD=4,则D到BC边的距离为.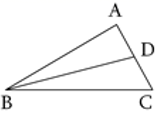
三、解答题
-
16. 如图是小明根据全班同学喜爱四类电视节目的人数而绘制的两幅不完整的统计图.请根据图中的信息,求出喜爱“体育”节目的人数.
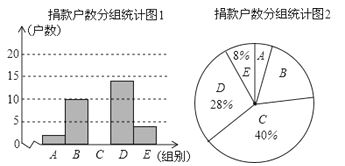
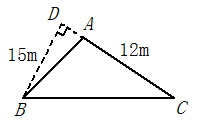
 17. 为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
17. 为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.组别
捐款额(x)元
户数
A
1≤x<50
a
B
50≤x<100
10
C
100≤x<150
D
150≤x<200
E
x≥200
请结合以上信息解答下列问题.
(1)a等于多少?本次调查样本的容量是多少?
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区有1500户住户,请根据以上信息估计,全社区捐款不少于150元的户数是多少?