（人教版）2022-2023学年八年级数学入学综合测试卷（二）

试卷更新日期：2022-07-05 类型：复习试卷

进入出卷网下载

一、单选题

1. 如果两条平行线被第三条直线所截，那么一组同位角的平分线的位置关系是（）

A、互相平行 B、互相垂直 C、相交但不垂直 D、平行或相交都有可能

查看试题解析
2. 如图，将一副三角板放在两条平行线之间，其中含 $45 °$ 角的三角板的直角边与含 $30 °$ 角的三角板的斜边共线，且 $45 °$ 角的顶点与角 $60 °$ 的顶点重合，则 $∠ 1$ 的度数是（）

A、 $130 °$ B、 $120 °$ C、 $135 °$ D、 $105 °$

查看试题解析
3. 下列命题中是真命题的是（）

A、对顶角相等 B、两点之间，直线最短 C、同位角相等 D、平面内有且只有一条直线与已知直线平行

查看试题解析
4. 将 $R t △ A B C$ 沿 $C B$ 方向平移后得到 $R t △ D E F$ ，已知 $A M = 3$ ， $B E = 6$ ， $D E = 10$ .则图中阴影部分的面积为（）

A、39 B、51 C、45 D、42

查看试题解析
5. 北京 2022年冬奥会会徽是以汉字“冬”为灵感来源设计的.在下面的四个图中，由下图经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，直线l₁、l₂分别与△ABC的两边AB、BC相交，且l₁∥l₂ ，若∠B＝35°，∠1＝105°，则∠2的度数为（）

A、45° B、50° C、40° D、60°

查看试题解析
7. 下列命题是真命题的个数为（）
①一个角的补角大于这个角.②三角形的内角和是180°.③若 $a^{2} = b^{2}$ ，则 $a = b$ .④相等的角是对顶角.⑤两点之间，线段最短.

A、2 B、3 C、4 D、5

查看试题解析
8. 在△ABC中，∠A＝∠B＝ $\frac{1}{4}$ ∠C，则∠C＝（）

A、70° B、80° C、100° D、120°

查看试题解析
9. 如图所示，一副三角板叠放在一起，则图中 $∠ α$ 等于（）

A、105° B、115° C、120° D、135°

查看试题解析
10. 如图，已知 $∠ A C D$ 为 $△ A B C$ 的外角， $∠ A C D = 60 °$ ， $∠ B = 20 °$ ，那么 $∠ A$ 的度数是（）

A、30° B、40° C、50° D、60°

查看试题解析

二、填空题

11. 如图，PC∥OA，PD∥OB，∠AOB＝ $\frac{1}{2}$ ∠CPD，则∠AOB=°.

查看试题解析
12. 如图，将 $△ A B C$ 沿 $B C$ 方向平移 $3 c m$ 得到 $△ D E F$ ，如果四边形 $A B F D$ 的周长是 $28 c m$ ，则 $△ D E F$ 的周长是 $c m$ ．

查看试题解析
13. 在△ABC中，若∠A＝35°，∠B＝65°，则∠C的度数为.

查看试题解析
14. 在△ABC中，已知∠B是∠A的2倍，∠C比∠A大20°，则∠A= ．

查看试题解析
15. 如图，已知 $△ A B C$ 中， $∠ C = 60 °$ ，BD平分 $∠ A B C$ ，AD平分外角 $∠ C A E$ ，则 $∠ D =$ 度.

查看试题解析

三、解答题

16. 如图，已知 $∠ 1 = ∠ 2$ ， $∠ B = ∠ C$ ，求证： $A B ∥ C D$ .
证明：∵ $∠ 1 = ∠ 2$ （已知），
又∵ $∠ 1 =$       ▲      （   ），
∴ $∠ 2 = ∠ F M N$ （等量代换）.
∴ $C F ∥ E B$ （   ）.
∴ $∠ C = ∠ B E D$ （   ）.
又∵ $∠ B = ∠ C$ （已知），
∴ $∠ B =$       ▲      （等量代换）.
∴ $A B ∥ C D$ （   ）.

查看试题解析
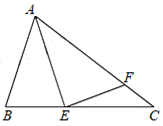
17. 已知命题：“如图，点B、F、C、E在同一条直线上，则AB∥DE．”判断这个命题是真命题还是假命题，如果是真命题，请给出证明；如果是假命题，在不添加其他辅助线的情况下，请添加一个适当的条件使它成为真命题，并加以证明．

查看试题解析
18. 如图是一块长方形的草地，长为21m.宽为15m.在草地上有两条宽为1米的小道，长方形的草地上除小道外长满青草.求长草部分的面积为多少？

查看试题解析
19. 两个直角三角板如图摆放，其中∠BAC＝∠EDF＝90°，∠E＝45°，∠C＝30°，AB与DF交于点M，BC $∥$ EF，求∠BMD的度数．

查看试题解析
20. 如图， $△ A B C$ 中， $∠ B = 2 ∠ C$ ， $A E$ 平分 $∠ B A C$ ．若 $E F ⊥ A E$ 交 $A C$ 于F ，求证： $∠ C = 2 ∠ F E C$ ．

查看试题解析
21. 如图，在 $△ A B C$ 中，点D、E分别在边AB、AC上，BE与CD交于点F， $∠ A = 62 °$ ， $∠ A C D = 25 °$ ， $∠ E F C = 53 °$ ．求 $∠ B D C$ 和 $∠ D B E$ 的度数．

查看试题解析
22. 如图，在△ABC中，D是BC边上一点，∠DAB＝∠DBA ， ∠ADC＝∠C ， ∠BAC＝75°，求：∠DAC的度数

查看试题解析