（人教版）2022-2023学年八年级数学入学综合测试卷（一）
试卷更新日期：2022-07-05 类型：复习试卷
一、单选题
-
1. 如图，直线AC，BD相交于点O，∠AOB=48°，则∠COD的度数是（ ）
A、42° B、48° C、96° D、132°2. 如图，下列说法错误的是（ ）
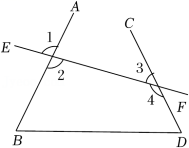A、∠1与∠2是对顶角 B、∠1与∠3是同位角 C、∠1与∠4是内错角 D、∠B与∠D是同旁内角3. 如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，则点C到AB的距离是线段（ ）的长度.
A、BD B、AD C、CD D、BC4. 下列说法：①相等的角是对顶角；②同位角相等；③过一点有且只有一条直线与已知直线平行；④直线外一点到这条直线的垂线段的长度，叫做点到直线的距离；其中正确的有（ ）个．A、0 B、1 C、2 D、35. 如图，下列条件中能判断AB∥CD的是（ ）
A、∠BAD+∠ABC＝180° B、∠BAC＝∠ACD C、∠1＝∠2 D、∠3＝∠46. 已知三角形的两边长分别为2cm和3cm，则第三边长可能是（ ）A、6cm B、5cm C、3cm D、1cm7. 如图， 于点D， 于点C， 于点F，下列关于高的说法错误的是（ ）
A、在 中， 是 边上的高 B、在 中， 是 边上的高 C、在 中， 是 边上的高 D、在 中， 是 边上的高8. 下列图形中，不具有稳定性的是（ ）A、等腰三角形 B、平行四边形 C、锐角三角形 D、等边三角形9. 如图，为估计池塘岸边A、B两点的距离，小方在池塘的一侧选取一点O，OA=15米，OB＝10米，A、B间的距离不可能是（ ）
A、5米 B、10米 C、15米 D、20米10. 利用直角三角板，作的高，下列作法正确的是（ ）A、
B、
C、
D、
二、填空题
-
11. 如图， ， ， 则表示点到直线所在直线的距离为线段的长度．
12. 如图，在条件：①；②；③；④中，能判断的条件是（填序号）．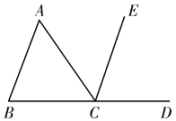
13. 已知三角形的三边分别为n，5，7，则n的范围是 .14. 用海伦公式求面积的计算方法是： ，其中S表示三角形的面积，a，b，c分别表示三边之长，p表示周长的一半，即 .我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致，所以这个公式也叫“海伦-秦九韶式” .请你利用公式解答下列问题.在 中，已知三边之长 ， ， ，则 的面积为.15. 如图，桥梁拉杆和桥面构成三角形的结构，根据的数学道理 ．
三、解答题
-
16. 如图，三条直线AB、CD、EF相交于点O，若∠3＝3∠2、∠2＝2∠1，求∠1、∠2、∠3的度数.
17. 如图所示，点O为直线BD上的一点，OC⊥OA，垂足为点O，∠COD=2∠BOC，求∠AOB的度数．
