江西省南昌市2022届高三理数第三次模拟测试试卷

试卷更新日期：2022-07-05 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | \frac{x - 2}{x} < 0}$ ， $B = {x | x^{2} + x - 2 > 0}$ ，则 $A ∩ B =$ （）

A、 $(- \infty ， 2)$ B、 $(- 2 ， 2)$ C、 $(1 ， 2)$ D、 $(- \infty ， 1)$

查看试题解析
2. 命题“若 $x$ ， $y$ 都是奇数，则 $x + y$ 是偶数”的逆否命题是（）

A、若 $x + y$ 不是偶数，则 $x$ ， $y$ 都不是奇数 B、若 $x + y$ 不是偶数，则 $x$ ， $y$ 不都是奇数 C、若 $x$ ， $y$ 都是偶数，则 $x + y$ 是奇数 D、若 $x$ ， $y$ 都不是奇数，则 $x + y$ 不是偶数

查看试题解析
3. 若复数 $z$ 的实部和虚部均为整数，则称复数 $z$ 为高斯整数，关于高斯整数，有下列命题：
①整数都是高斯整数；②两个高斯整数的乘积也是高斯整数；③模为3的非纯虚数可能是高斯整数；④只存在有限个非零高斯整数 $z$ ，使 $\frac{1}{z}$ 也是高斯整数
其中正确的命题有（）

A、①②④ B、①②③ C、①② D、②③④

查看试题解析
4. 某工厂研究某种产品的产量 $x$ （单位：吨）与某种原材料的用量 $y$ （单位：吨）之间的相关关系，在生产过程中收集了4组数据如表所示：
$x$
3
4
6
7
$y$
2.5
3
4
5.9
根据表中的数据可得回归直线方程 $\hat{y} = 0.78 x + a$ ，有下列说法：① $x$ 与 $y$ 正相关；② $y$ 与 $x$ 的相关系数 $r < 0$ ；③ $a = - 0.05$ ；④产量为8吨时预测原材料的用量约为6.19吨.其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 某正方体被截去部分后得到的空间几何体的三视图如图所示，则该空间几何体的体积为（）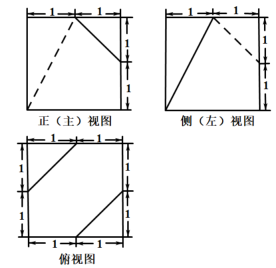

A、 $\frac{13}{2}$ B、 $\frac{22}{3}$ C、 $\frac{15}{2}$ D、 $\frac{23}{3}$

查看试题解析
6. 已知两条直线 $l_{1}$ ： $2 x - 3 y + 2 = 0$ ， $l_{2}$ ： $3 x - 2 y + 3 = 0$ ，有一动圆（圆心和半径都在变动）与 $l_{1}$ ， $l_{2}$ 都相交，并且 $l_{1}$ ， $l_{2}$ 被截在圆内的两条线段的长度分别是定值26，24，则动圆圆心的轨迹是（）

A、圆 B、椭圆 C、双曲线 D、直线

查看试题解析
7. 已知实数 $x ， y ， z$ 满足 $l n x = e^{y} = \frac{1}{z}$ ，则下列关系式不可能成立的是（）

A、 $x > y > z$ B、 $x > z > y$ C、 $z > x > y$ D、 $z > y > x$

查看试题解析
8. 科学记数法是一种记数的方法.把一个数 $x$ 表示成 $a$ 与10的 $n$ 次幂相乘的形式，其中 $1 \leq a < 10$ ， $n \in N$ .当 $x > 0$ 时， $l g x = k + l g a$ .若 $l g 2 \approx 0.301$ ，则数列 ${2^{n}}$ 中的项是七位数的有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
9. 已知 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ， $A = \frac{π}{3}$ ， $c = 3$ ， $a s i n B = \sqrt{3}$ . $D$ ， $E$ 分别为线段 $A B$ ， $A C$ 上的动点， $\frac{A D}{A B} = \frac{C E}{C A}$ ，则 $D E$ 的最小值为（）

A、 $\frac{\sqrt{7}}{2}$ B、 $\frac{\sqrt{5}}{2}$ C、 $\frac{3 \sqrt{57}}{19}$ D、 $\frac{2 \sqrt{57}}{19}$

查看试题解析
10. 已知双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别是 $F_{1}$ ， $F_{2}$ ， $P$ 是双曲线右支上一点，且 $P F_{2} ⊥ F_{1} F_{2}$ ， $I$ 和 $G$ 分别是 $△ P F_{1} F_{2}$ 的内心和重心，若 $I G$ 与 $x$ 轴平行，则双曲线的离心率为（）

A、 $\sqrt{3}$ B、2 C、3 D、4

查看试题解析
11. 设 $a > 0$ ， $b > e$ ， $f (x) = (x - a - 1) e^{x} - b (\frac{x^{3}}{3} - \frac{a x^{2}}{2})$ （ $e$ 为自然对数的底数），若 $x = a$ 不是函数 $f (x)$ 的极值点，则 $\frac{b}{a}$ 的最小值为（）

A、 $e$ B、 $\frac{e^{2}}{4}$ C、 $\frac{e^{3}}{9}$ D、 $\frac{e^{\sqrt{2}}}{2}$

查看试题解析
12. 已知长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = 2$ ， $B C = 2 \sqrt{2}$ ， $A A_{1} = 3$ ， $P$ 为矩形A₁B₁C₁D₁内一动点，设二面角 $P - A D - C$ 为 $α$ ，直线 $P B$ 与平面 $A B C D$ 所成的角为 $β$ ，若 $α = β$ ，则三棱锥 $P - A_{1} B C_{1}$ 体积的最小值是（）

A、 $\sqrt{2}$ B、 $3 \sqrt{2} - 1$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{3 \sqrt{2}}{2}$

查看试题解析

二、填空题

13. 已知 $\vec{a} = (1 ， - \sqrt{3})$ ， $\vec{b} = (1 ， 2 - \sqrt{3})$ ，则向量 $\vec{a}$ 与 $\vec{a} - \vec{b}$ 的夹角为.

查看试题解析
14. 已知实数 $x$ ， $y$ 满足约束条件 ${\begin{array}{l} x - y + 1 \geq 0 \\ x + 3 y + 5 \geq 0 \\ x \leq 1 \end{array}$ ，则 $z = x + y$ 的最小值为.

查看试题解析
15. 已知函数 $f (x) = {\begin{array}{l} 2 l n x - x^{2} (x > 0) \\ x + \frac{a}{x} (x < 0) \end{array}$ 的最大值为-1，则实数 $a$ 的取值范围是.

查看试题解析
16. 已知函数 $f (x) = s i n (c o s x) + c o s x$ ，现有以下说法：
①直线 $x = π$ 是 $f (x)$ 图象的一条对称轴；
② $f (x)$ 在 $[π ， 2 π]$ 单调递增；
③ $\exists x \in R$ ， $f (x) \geq 1 + \frac{\sqrt{6} + \sqrt{2}}{4}$ .
则上述说法正确的序号是.

查看试题解析

三、解答题

17. 已知数列 ${a_{n}}$ 为等比数列，且 $a_{1} = 1$ ， $a_{n} a_{n + 1} = - 2^{2 n - 1}$ .

(1)、求 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = \frac{(- 1)^{n} \cdot n}{a_{n}}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $S_{n}$ .

查看试题解析
18. 如图，正方形 $A B C D$ 所在的平面与菱形 $A B E F$ 所在的平面互相垂直， $△ A E F$ 为等边三角形.

(1)、求证： $A E ⊥ C F$ ；

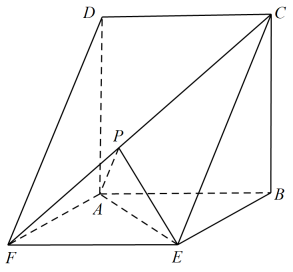(2)、 $\vec{F P} = λ \vec{F C} (0 \leq λ \leq 1)$ ，是否存在 $λ$ ，使得平面 $P A E ⊥$ 平面 $D C E F$ ，若存在，求出 $λ$ 的值，若不存在，请说明理由.

查看试题解析
19. 已知椭圆 $C$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{3}}{2}$ ，点 $T (2 ， 1)$ 在椭圆上，与 $O T$ 平行的直线 $l$ 交椭圆 $C$ 于 $P$ ， $Q$ 两点，直线 $T P$ ， $T Q$ 分别于 $x$ 轴正半轴交于 $M$ ， $N$ 两点.

(1)、求椭圆 $C$ 的标准方程；

(2)、求证： $| O M | + | O N |$ 为定值.

查看试题解析
20. 甲、乙两名选手争夺一场乒乓球比赛的冠军.比赛采取三局两胜制，即某选手率先获得两局胜利时比赛结束，且该选手夺得冠军.根据两人以往对战的经历，甲、乙在一局比赛中获胜的概率分别为 $\frac{3}{5}$ ， $\frac{2}{5}$ ，且每局比赛的结果相互独立.

(1)、求甲夺得冠军的概率；

(2)、比赛开始前，工作人员买来一盒新球，共有6个.新球在一局比赛中使用后成为“旧球”，“旧球”再在一局比赛中使用后成为“废球”.每局比赛前裁判员从盒中随机取出一颗球用于比赛，且局中不换球，该局比赛后，如果这颗球成为废球，则直接丢弃，否则裁判员将其放回盒中.记甲、乙决出冠军后，盒内新球的数量为X，求随机变量X的分布列与数学期望.

查看试题解析
21. 已知函数 $f (x) = e^{x} - \frac{1}{2} a x^{2} - x - 1 (x > 0 ， a \in R)$ .

(1)、当 $a = 1$ 时，判断 $f (x)$ 的单调性；

(2)、若 $a > 1$ 时，设 $x_{1}$ 是函数 $f (x)$ 的零点， $x_{0}$ 为函数 $f (x)$ 极值点，求证： $x_{1} - 2 x_{0} < 0$ .

查看试题解析
22. 已知直线 $l$ 的参数方程为： ${\begin{array}{l} x = \frac{\sqrt{2}}{2} t \\ y = 2 + \frac{\sqrt{2}}{2} t \end{array}$ （ $t$ 为参数），曲线 $C$ 的极坐标方程为： $ρ^{2} = \frac{7}{1 + 2 s i n 2 θ}$ .

(1)、写出直线 $l$ 的普通方程和曲线 $C$ 的直角坐标方程；

(2)、已知直线 $l$ 和曲线 $C$ 交于 $A ， B$ 两点，设点 $M (0 ， 2)$ ，求 $\frac{1}{| M A |} + \frac{1}{| M B |}$ .

查看试题解析
23. 已知函数 $f (x) = | x - 2 | + | x - 4 |$ ，已知不等式 $f (x) \geq k x (k > 0)$ 恒成立.

(1)、求 $k$ 的最大值 $k_{0}$ ；

(2)、设 $a > 0$ ， $b > 0$ ，求证： $\frac{a}{a + 2 b} + \frac{b}{2 a + b} \geq \frac{1}{3 k_{0}}$ .

查看试题解析

$x$	3	4	6	7
$y$	2.5	3	4	5.9