广西百色市2022年中考数学试卷

试卷更新日期：2022-07-05 类型：中考真卷

进入出卷网下载

一、单选题

1. ﹣2023的绝对值等于（）

A、﹣2023 B、2023 C、土2023 D、2022

查看试题解析
2. $\frac{3}{5}$ 的倒数是（）

A、 $\frac{5}{3}$ B、 $\frac{3}{5}$ C、 $- \frac{3}{5}$ D、 $- \frac{5}{3}$

查看试题解析
3. 篮球裁判员通常用抛掷硬币的方式来确定哪一方先选场地，那么抛掷一枚均匀的硬币一次，正面朝上的概率是（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
4. 方程3x＝2x＋7的解是（）

A、x＝4 B、x＝﹣4 C、x＝7 D、x＝﹣7

查看试题解析
5. 下列几何体中，主视图为矩形的是（）

A、 B、 C、 D、

查看试题解析
6. 已知△ABC与△A₁B₁C₁是位似图形，位似比是1：3，则△ABC与△A₁B₁C₁的面积比（）

A、1 ：3 B、1：6 C、1：9 D、3：1

查看试题解析
7. 某班一合作学习小组有5人，某次数学测试成绩数据分别为65、78、86、91、85，则这组数据的中位数是（）

A、78 B、85 C、86 D、91

查看试题解析
8. 下列图形中，既是中心对称图形又是轴对称图形的是（）

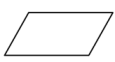A、平行四边形 B、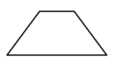等腰梯形 C、正三角形 D、圆

查看试题解析
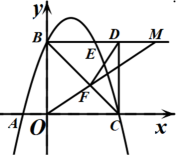
9. 如图，是求作线段AB中点的作图痕迹，则下列结论不一定成立的是（）

A、∠B＝45° B、AE＝EB C、AC＝BC D、AB⊥CD

查看试题解析
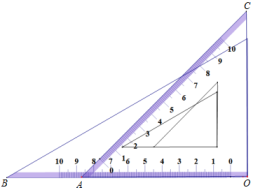
10. 如图，在△ABC中，点A（3，1），B（1，2），将△ABC向左平移2个单位，再向上平移1个单位，则点B的对应点B′的坐标为（）

A、（3，-3） B、（3，3） C、（－1，1） D、（－1，3）

查看试题解析
11. 如图，是利用割补法求图形面积的示意图，下列公式中与之相对应的是（）

A、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ B、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$ C、 $(a + b) (a - b) = a^{2} - b^{2}$ D、 $(a b)^{2} = a^{2} b^{2}$

查看试题解析
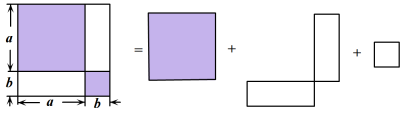12. 活动探究：我们知道，已知两边和其中一边的对角对应相等的两个三角形不一定全等，如已知△ABC中，∠A＝30°， AC＝3，∠A所对的边为 $\sqrt{3}$ ，满足已知条件的三角形有两个（我们发现其中如图的△ABC是一个直角三角形），则满足已知条件的三角形的第三边长为（）

A、 $2 \sqrt{3}$ B、 $2 \sqrt{3} - 3$ C、 $2 \sqrt{3}$ 或 $\sqrt{3}$ D、 $2 \sqrt{3}$ 或 $2 \sqrt{3} - 3$

查看试题解析

二、填空题

13. 负数的概念最早出现在中国古代著名的数学专著《九章算术》中，负数与对应的正数“数量相等，意义相反”，如果向东走了5米，记作＋5米，那么向西走5米，可记作米.

查看试题解析
14. 因式分解： $a x + a y =$ .

查看试题解析
15. 如图摆放一副三角板，直角顶点重合，直角边所在直线分别重合，那么∠BAC的大小为

查看试题解析
16. 数学兴趣小组通过测量旗杆的影长来求旗杆的高度，他们在某一时刻测得高为2米的标杆影长为1.2米，此时旗杆影长为7.2米，则旗杆的高度为米.

查看试题解析
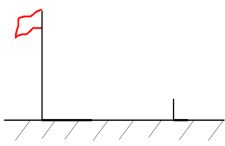17. 小韦同学周末的红色之旅，坐爸爸的车去百色起义纪念馆，从家里行驶7千米后，进入高速公路，在高速公路上保持匀速行驶，小韦记录高速公路上行驶的时间（和路程）数据如下表，按照这个速度行驶了2小时进入高速路出口匝道，再行驶5千米抵达纪念馆，则小韦家到纪念馆的路程是千米.

t小时

0.2

0.6

0.8

s千米

20

60

80

查看试题解析
18. 为落实立德树人，发展素质教育，加强美育，需要招聘两位艺术老师，从学历、笔试、上课和现场答辩四个项目进行测试，以最终得分择优录取，甲、乙、丙三位应聘者的测试成绩（10分制）如表所示，如果四项得分按照“1：1：1：1”比例确定每人的最终得分，丙得分最高，甲与乙得分相同，分不出谁将被淘汰；鉴于教师行业应在“上课“项目上权重大一些（其他项目比例相同），为此设计了新的计分比例，你认为三位应聘者中（填：甲、乙或丙）将被淘汰.
成绩
应聘者

甲

乙

丙
学历
9
8
9
笔试
8
7
9
上课
7
8
8
现场答辩
8
9
8

查看试题解析

三、解答题

19. 计算： $3^{2} + {(- 2)}^{0} - 17$

查看试题解析
20. 解不等式2x＋3 $\geq$ －5，并把解集在数轴上表示出来.

查看试题解析
21. 已知：点 A（1，3）是反比例函数 $y_{1} = \frac{k}{x}$ （k≠0）的图象与直线 $y_{2} = m x$ （ m≠0）的一个交点.

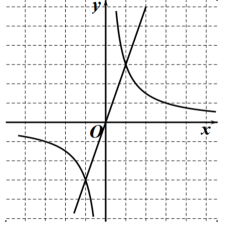(1)、求k 、m的值：

(2)、在第一象限内，当 $y_{2} > y_{1}$ 时，请直接写出x的取值范围

查看试题解析
22. 校园内有一块四边形的草坪造型，课外活动小组实地测量，并记录数据，根据造型画如图的四边形ABCD，其中 AB＝CD＝2米，AD＝BC＝3米，∠B＝ $30 °$

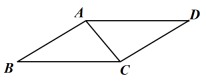(1)、求证：△ABC≌△CDA ；

(2)、求草坪造型的面积.

查看试题解析
23. 学校举行“爱我中华，明诵经典”班级朗诵比赛，黄老师收集了所有参赛班级的成绩后，把成绩x（满分100分）分成四个等级（A：90≤x≤100，B：80≤x＜90，C：70≤x＜80，D：60≤x＜70）进行统计，并绘制成如下不完整的条形统计图和扇形统计图.根据信息作答：

(1)、参赛班级总数有个；m＝

(2)、补全条形统计图：

(3)、统计发现D等级中七年级、八年级各有两个班，为了提高D等级班级的朗诵水平，语文组老师计划从D等级班级中任选两个班进行首轮培训，求选中两个班恰好是同一个年级的概率（用画树状图或列表法把所有可能结果表示出来）.

查看试题解析
24. 金鷹酒店有140间客房需安装空调，承包给甲、乙两个工程队合作安装，每间客房都安装同一品牌同样规格的一台空调，已知甲工程队每天比乙工程队多安装5台，甲工程队的安装任务有80台，两队同时安装.问：

(1)、甲，乙两个工程队每天各安装多少台空调，才能同时完成任务？

(2)、金鹰酒店响应“縁色环保”要求，空调的最低温度设定不低于26℃，每台空调每小时耗电1.5度：据预估，每天至少有100间客房有旅客住宿，旅客住宿时平均每天开空调约8小时，若电费0.8元／度，请你估计该酒店毎天所有客房空调所用电费 W（单位：元）的范围？

查看试题解析
25. 如图，AB为圆的直径， C是⊙O上一点，过点C的直线交AB的延长线于点M.作AD⊥MC，垂足为D，已知AC平分∠MAD .

(1)、求证：MC是⊙O的切线：

(2)、若 AB＝BM＝4，求 tan∠MAC的值

查看试题解析
26. 已知抛物线经过A（－1，0）、B（0、3）、 C（3，0）三点，O为坐标原点，抛物线交正方形OBDC的边BD于点E，点M为射线BD上一动点，连接OM ，交BC于点F

(1)、求抛物线的表达式；

(2)、求证：∠BOF＝∠BDF ：

(3)、是否存在点M使△MDF为等腰三角形？若不存在，请说明理由；若存在，求ME的长

查看试题解析

成绩应聘者	甲	乙	丙
学历	9	8	9
笔试	8	7	9
上课	7	8	8
现场答辩	8	9	8

t小时	0.2	0.6	0.8
s千米	20	60	80