2022-2023学年浙教版数学九年级上册2.3 用频率估计概率 同步练习
试卷更新日期：2022-07-05 类型：同步测试
一、单选题
-
1. 下表记录了一名球员在罚球线上投篮的结果：
投篮次数
50
100
150
200
250
400
500
800
投中次数
28
63
87
122
148
242
301
480
投中频率
0.560
0.630
0.580
0.610
0.592
0.605
0.602
0.600
根据频率的稳定性，估计这名球员投篮一次投中的概率约是（ ）
A、0.560 B、0.580 C、0.600 D、0.6202. 在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同．小明每次摸一个后放回再摸，通过多次试验发现，摸出红球的频率稳定在左右，则袋子中红球的个数最有可能是（ ）A、8 B、5 C、12 D、153. 甲、乙两位同学在一次用频率去估计概率的实验中统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的实验可能是（ ）
A、掷一枚正六面体的骰子，出现1点的概率 B、一个袋子中有2个白球和1个红球，从中任取一个球，则取到红球的概率 C、抛一枚硬币，出现正面的概率 D、任意写一个整数，它能被2整除的概率4. 在一个不透明的袋中装有仅颜色不同的白球和红球共20个，某学习小组做摸球试验，将球搅匀后从中随机摸出一个球，记下颜色后再放回袋中；然后重复上述步骤……如表是实验中记录的部分统计数据：摸球次数
10
40
80
200
500
800
摸到红球次数
3
16
20
40
100
160
摸到红球的频率
0.3
0.4
0.25
0.2
0.2
0.2
则袋中的红球个数可能有（ ）
A、16个 B、8个 C、4个 D、2个5. 在抛掷一枚质地均匀的硬币的实验中，第100次抛掷时，反面朝上的概率是（ ）A、 B、 C、 D、不确定6. 绿豆在相同条件下的发芽试验，结果如下表所示：每批粒数n
100
300
400
600
1000
2000
3000
发芽的粒数m
96
282
382
570
948
1912
2850
发芽的频率
0.960
0.940
0.955
0.950
0.948
0.956
0.950
则绿豆发芽的概率估计值（精确到0.01）是（ ）
A、0.96 B、0.95 C、0.94 D、0.907. 如图，是某射手在相同条件下进行射击训练的结果统计图，该射手击中靶心的概率的估计值为（ ）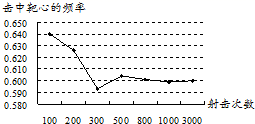
A、0.600 B、0.640 C、0.595 D、0.6058. 小明在一次用“频率估计概率”的实验中，把对联“海水朝朝朝朝朝朝朝落，浮云长长长长长长长消”中的每个汉字分别写在同一种卡片上，然后把卡片无字的面朝上，随机抽取一张，并统计了某一结果出现的频率，绘制了如图所示的折线统计图，则符合这一结果的实验最有可能是（ ）
A、抽出的是“朝”字 B、抽出的是“长”字 C、抽出的是独体字 D、抽出的是带“氵”的字9. 某林业局将一种树苗移植成活的情况绘制成如下统计图，由此可估计这种树苗移植成活的概率约为（ ）
A、0.95 B、0.90 C、0.85 D、0.8010. 一个密闭不透明的盒子里有若干个白球，在不许将球倒出来数的情况下，为了估计白球数，小刚向其中放入了8个黑球，搅匀后从中随意摸出一个球记下颜色，再把它放回盒中，不断重复这一过程，共摸球400次，其中80次摸到黑球，你估计盒中大约有白球（ ）A、32个 B、36个 C、40个 D、42个二、填空题
-
11. 一个不透明的盒子中装有8个白球和若干个红球，它们除颜色不同外，其余均相同，从盒子中随机摸出一球记下其颜色，再把它放回盒子中摇匀，重复上述过程，共试验1000次，其中有199次摸到红球，由此估计盒子中的红球大约有个．12. 一水塘里有鲤鱼、鲢鱼共10000条，一渔民通过多次捕捞实验后发现，鲤鱼出现的频率为30%，则水塘有鲢鱼 条．
13. 社团课上，同学们进行了“摸球游戏”：在一个不透明的盒子里，装有20个除颜色不同外其余均相同的黑、白两种球，将盒子里面的球搅匀后，从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程．整理数据后，制作了“摸出黑球的频率”与“摸球的总次数”的关系图象，如图所示，经分析可以推断“摸出黑球”的概率约为 ．
14. 综合实践小组的同学们在相同条件下做了测定某种黄豆种子发芽率的实验，结果如表所示：
黄豆种子数（单位：粒）
800
1000
1200
1400
1600
1800
2000
发芽种子数（单位：粒）
762
948
1142
1331
1518
1710
1902
种子发芽的频率（结果保
留至小数点后三位）
0.953
0.948
0.952
0.951
0.949
0.950
0.951
那么这种黄豆种子发芽的概率约为（精确到0.01）
15. 如图为测量平地上一块不规则区域(图中的阴影部分)的面积，画一个边长为5m的正方形，使不规则区域落在正方形内，现向正方形内随机投掷小石子(假设小石子落在正方形内每一点都是等可能的)，经过大量重复投掷试验，发现小石子落在不规则区域的频率稳定在常数0.2附近，由此可估计不规则区域的面积是m2.
16. 某瓷砖厂在相同条件下抽取部分瓷砖做耐磨试验，结果如下表所示：抽取瓷砖数 n 100 300 400 600 1000 2000 3000 合格品数 m 96 282 382 570 949 1906 2850 合格品频率 0.960 0.940 0.955 0.950 0.949 0.953 
0.950 则这个厂生产的瓷砖是合格品的概率估计值是（精确到0.01）。
17. 一个不透明的盒子里有若干个白球，在不允许将球倒出来的情况下，为估计白球的个数，小刚向其中放入8个黑球，摇匀后从中随机摸出一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中88次摸到黑球，估计盒中大约有白球个．
18. 某商场举办抽奖活动，每张奖券获奖的可能性相同，以10000奖券为一个开奖单位，设特等奖10个，一等奖100个，二等奖500个，则1张奖券中奖的概率是 ．19. 同学们设计了一个用计算机模拟随机重复抛掷瓶盖的实验，记录盖面朝上的次数，并计算盖面朝上的频率，下表是依次累计的实验结果．抛掷次数
500
1000
1500
2000
3000
4000
5000
盖面朝上次数
275
558
807
1054
1587
2124
2650
盖面朝上频率
0.550
0.558
0.538
0.527
0.529
0.531
0.530
下面有两个推断：
①随着实验次数的增加，“盖面朝上”的频率总在0.530附近，显示出一定的稳定性，可以估计“盖面朝上”的概率是0.530；
②若再次用计算机模拟此实验，则当投掷次数为1000时，“盖面朝上”的频率不一定是0.558；
其中合理的推断的序号是： ．
20. 某射手在相同条件下进行射击训练，结果如下：射击次数n
10
20
40
50
100
200
500
1000
击中靶心的频数m
9
19
37
45
89
181
449
901
击中靶心的频率
0.900
0.950
0.925
0.900
0.890
0.905
0.898
0.901
该射手击中靶心的概率的估计值是.
三、解答题
-
21. 某工厂生产的一批零件，出现次品的概率为5%，若生产这种零件10000个，大约出现次品多少个？22. 4件同型号的产品中，有1件不合格品和3件合格品.在这4件产品中加入 件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的频率稳定在0.95，由此可以推算出 的值大约是多少？23. 一个口袋中放有16个球，其中红球6个，白球和黑球各若干个，每个球除了颜色外没有任何区别.小明通过大量反复的试验（每次将球搅匀后，任意摸出一个球记下颜色后再放回）发现，取出黑球的频率稳定在 附近，请你估计袋中白球的个数24. 某人承包了一池塘养鱼，他想估计一下收入情况.于是让他上初三的儿子帮忙.他儿子先让他从鱼塘里随意打捞上了60条鱼，把每条鱼都作上标记，放回鱼塘；过了2天，他让他父亲从鱼塘内打捞上了50条鱼，结果里面有2条带标记的.假设当时这种鱼的市面价为2.8元/斤，平均每条鱼估计2.3斤，你能帮助他估计一下今年的收入情况吗?
25. 南校区本学期对初三学生体育选考项目---引体向上（仅男生项目）进行抽样调查，已知完成15个可以拿到100分，完成23个为最高120分，A表示学生做引体向上23个或以上，B表示做15-22个，C表示做10-14个，D表示做9个或9个以下.根据调查结果绘制了不完整的统计图.成绩
频数（人数）
频率
A
28
x
B
14
0.2
C
m
0.3
D
n
y
(1)、抽样学生数为人，x= ， y=；(2)、补全条形统计图；(3)、若南校区初三共有720名学生，男女比例为7：5，请估计一共有多少学生可以拿到100分及以上？四、综合题
-
26. 在某项针对18～35岁的青年人每天发微博数量的调查中，设一个人的“日均发微博条数”为m，规定：当m≥10时为A级，5≤m＜10时为B级，当0≤m＜5为C级．现随机抽取30个符合年龄条件的青年人开展“每人日均发微博条数”的调查，所有抽青年人的“日均发微博条数”的数据如表：
11
10
6
15
9
16
13
12
0
8
2
8
10
17
6
13
7
5
7
3
12
10
7
11
3
6
8
14
15
12
(1)、求样本数据中为A级的频率；(2)、试估计1000个18～35岁的青年人中“日均发微博条数”为A级的人数；(3)、从样本数据为C级的人中随机抽取两人，用列举法求抽得两个人的“日均发微博条数”都是3的概率．27. 在一个不透明的盒子里装着只有颜色不同的黑、白两种球共5个，小明做摸球实验，他将盒子里面的球搅匀后从中随机摸出一球记下颜色，再把它放回盒子，不断重复上述过程实验n次，下表是小明“摸到白球”的频数、频率统计表.摸球实验次数n
10
100
150
200
500
…
摸到白球的频数m
2
22
31
39
101
…
摸到白球的频率p
0.200
0.220
0.207
0.195
0.202
…
(1)、观察上表，可以推测，摸一次摸到白球的概率为.(2)、请你估计盒子里白球个数.(3)、若往盒子中同时放入x个白球和y个黑球，从盒子中随机取出一个白球的概率是0.25，求y与x之间的函数关系式.28. 在一只不透明的袋子中装有黑球、白球共10个，这些球除颜色外都相同，小明每次摇匀后随机从袋中摸出一个球，记录颜色后放回袋中，通过2000次重复摸球实验后，共摸出黑球1205次．(1)、估计袋中有黑球个；(2)、小明从袋中取出n个黑球后，小明从袋中剩余的球中随机摸出一个球是黑球的概率为 ，求n的值．29. 有一个圆形转盘，分黑色、白色两个区域.(1)、某人转动转盘，对指针落在黑色区域或白色区域进行了大量试验，得到数据如下表：实验次数n(次)
10
100
2000
5000
10000
50000
100000
白色区域次数m(次)
3
34
680
1600
3405
16500
33000
落在白色区域频率
0.3
0.34
0.34
0.32
0.34
0.33
0.33
请你利用上述实验，估计转动该转盘指针落在白色区域的概率为
(2)、若该圆形转盘白色扇形的圆心角为120度，黑色扇形的圆心角为240°，转动转盘两次，求指针一次落在白色区域，另一次落在黑色区域的概率.30. 一个不透明的袋中装有黄球、黑球和红球共40个，它们除颜色外都相同，其中红球有22个，且经过大量试验发现摸出一个球为黄球的频率接近0.125.(1)、求袋中有多少个黑球；(2)、现从袋中取出若干个黑球，并放入相同数量的黄球，搅拌均匀后使从袋中摸出一个球是黄球的概率达到 ，问取出了多少个黑球？