2022-2023学年浙教版数学九年级上册2.2 简单事件的概率 同步练习
试卷更新日期：2022-07-05 类型：同步测试
一、单选题
-
1. 下列说法正确的是（ ）A、“经过有交通信号的路口遇到红灯”是必然事件 B、已知某篮球运动员投篮投中的概率为0.6，则他投10次一定可投中6次 C、“心想事成，万事如意”描述的事件是随机事件 D、天气预报显示明天为阴天，那么明天一定不会下雨2. 掷一枚质地均匀的硬币10次，下列说法正确的是（ ）A、每2次必有一次正面朝上 B、必有5次正面朝上 C、可能有7次正面朝上 D、不可能有10次正面朝上3. 一个不透明的口袋中有三个完全相同的小球，把它们分别标号1、2、3，随机摸出一个小球不放回，再随机摸出一个小球，两次摸出的小球标号之和为5的概率是（ ）A、 B、 C、 D、4. 连续两次掷一枚质地均匀的硬币，两次都是正面朝上的概率是 （ ）A、 B、 C、 D、5. 不透明袋中装有3个红球和5个绿球，这些球除颜色外无其他差别.从袋中随机摸出1个球是红球的概率为（ ）A、 B、 C、 D、6. 在如图所示的电路中，随机闭合开关S1、S2、S3中的两个，能让灯泡L1发光的概率是（ ）
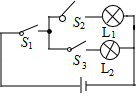A、 B、 C、 D、7. 中国福利彩票“双色球”投注方法是每注选择6个红色球号码（从1－33的33个数中选择）加一个蓝色球号码（从1－16中16个数中选择），若最近三期蓝色号码球的开奖结果都为奇数，则下一期蓝色球的开奖结果（ ）A、还是奇数 B、一定是偶数 C、是偶数的概率大于是奇数的概率 D、是偶数的概率为8. 一个质地均匀的小正方体，六个面上分别标有数字1、2、3、4、5、6，掷小正方体后，观察朝上一面的数字出现偶数的概率是（ ）A、 B、 C、 D、9. 不透明的布袋内装有形状、大小、质地完全相同的1个白球，2个红球，3个黑球，若随机摸出一个球恰是黑球的概率为（ ）A、 B、 C、 D、10. 一个不透明的口袋里有红、黄、蓝三种颜色的小球共9个，这些球除颜色外完全相同，其中有3个黄球，2个蓝球.则随机摸出一个红球的概率为（ ）A、 B、 C、 D、二、填空题
-
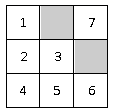
11. 20瓶饮料中有2瓶己过了保质期，从20瓶饮料中任取1瓶，取到己过保质期的饮料的概率是.12. 如图，在3×3的正方形网格中，已有两个小正方形被涂黑，再将图中剩余的编号为1～7的小正方形中任意一个涂黑，则所得图案是一个轴对称图形的概率是.
13. 从2021年起，湖南普通高校招生考试实行“3+1+2”模式：“3”是指语文，数学，外语3科为必选科目，“1”是指在物理，历史2科中任选1科，“2”是指在化学，生物，思想政治，地理4科中任选2科.若小玲在“1”中选择了历史，在“2”中已选择了地理，则她选择生物的概率是.14. 抛掷一枚质地均匀的硬币，若第一次是正面朝上，则第二次正面朝上的概率为 ．15. 在0，1，2，3，4，5这六个数中，随机取出一个数记为a，使得关于x的一元二次方程 有实数解的概率是.16. 国庆期间，小明从《长津湖》、《我和我的父辈》、《皮皮鲁与鲁西西》三部电影中随机选择一部观看，则选择《长津湖》观看的概率为 ；17. 一个布袋里装有2个只有颜色不同的球，其中1个红球，1个白球，从布袋里摸出1个球，记下颜色后放回，搅匀，再摸出1个球，则两次摸到的球恰好颜色不同的概率是 ．18. 有4张背面相同的纸牌A，B，C，D，其正面分别画有四个不同的几何图形（如图）．将这4张纸牌背面朝上洗匀后先由小明从中任意摸出一张，放回洗匀后再由小敏从中任意摸出一张，则“小明所摸纸牌是中心对称图形，小敏所摸纸牌是轴对称图形”的概率为 ．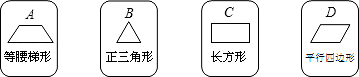
19. 某中学举办庆祝中国共产党建党100周年党史知识竞赛．某班有5名学生报名，其中2男3女，计划从这5名学生中随机抽选两名学生参加知识竞赛，所选两名学生中恰好1男1女的概率为 ．20. 已知盒子里有2个黄色球和n个红色球，每个球除颜色外均相同，现从中任取一个球，取出红色球的概率是 ，则n是.三、解答题
-
21. 甲、乙、丙三人相互传球，由乙开始发球，并作为第一次传球．用列表或画树状图的方法求经过3次传球后，球仍回到乙手中的概率．22.
将下面事件的字母写在最能代表它的概率的点上．
A：投掷一枚硬币时，得到一个正面；B：在一小时内，你步行可以走80千米；
C：给你一个骰子中，你掷出一个3；D：明天太阳会升起来．
23. 某航班约有a名乘客．在一次飞行中飞机失事的概率P=5×10﹣5 ． 一家保险公司要为乘客保险，许诺飞机一旦失事，向每位乘客赔偿50万元人民币．平均来说，保险公司应如何收取保费呢？24. 某商场举办购物有奖活动，在商场购满价值50元的商品可抽奖一次，丽丽在商场购物共花费120元，按规定抽了两张奖券，结果其中一张中了奖，能不能说商场的抽奖活动中奖率为50%？为什么？25. 李华的妈妈在她上学的时候总是叮嘱她：“注意交通安全，别被来往的车辆碰着！”但李华心里很不服气，心想：城里有一百多万人口，每天交通事故只有几起，事故发生的可能性太小了，概率几乎是零，你认为李华的想法对吗？为什么？四、综合题
-
26. 子怡的爸爸积极参加社区抗疫志愿服务工作，根据社区安排，志愿者被随机分到A组（体温检测）、B组（便民代购）和C组（环境消杀）．(1)、子怡爸爸被分到B组的概率是；(2)、某中学李老师也参加了该社区的志愿者队伍，请用画树状图或列表的方法求李老师和子恰的爸爸被分到同组的概率是多少？27. 某校组织八年级部分学生开展庆“五·四”演讲比赛，赛后对全体参赛学生成绩按A、B、C、D四个等级进行整理，得到下列不完整的统计图表．
等级
频数
频率
A
4
0.08
B
20
a
C
b
0.3
D
11
0.22
请根据所给信息，解答下列问题：
(1)、参加此次演讲比赛的学生共有人，a= ， b= ．(2)、请计算扇形统计图中B等级对应的扇形的圆心角的度数；(3)、已知A等级四名同学中包括来自同一班级的甲、乙两名同学，学校将从这四名同学中随机选出两名参加县级比赛，请用列表法或树状图，求甲、乙两名同学都被选中的概率．28. 某城市体育中考项目分为必测项目和选测项目，必测项目为：跳绳、立定跳远；选测项目为50米、实心球、踢毽子三项中任选一项．
(1)、每位考生将有种选择方案；(2)、用画树状图或列表的方法求小颖和小华将选择同种方案的概率．29. 在甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2；乙袋中装有3个完全相同的小球，分别标有数字﹣1，﹣2，0；现从甲袋中随机抽取一个小球，记录标有的数字为x，再从乙袋中随机抽取一个小球，记录标有的数字为y，确定点M坐标为（x，y）．(1)、用树状图或列举法列举点M所有可能的坐标；
(2)、求点M（x，y）在函数y=-x+1的图象上的概率；30. 科比•布莱恩特是美国职业篮球联盟NBA最好的得分手之一，他的中远距离跳投一直是教科书般的存在．如果他每次面对防守球员直接跳投命中的概率为 ， 请问：(1)、他面对防守球员连续三次跳投都命中的概率(2)、假设他第一次面对防守球员直接跳投，第二次是空位跳投（面前没有任何防守球员），而这两次都能命中的概率为 ， 那么他每次空位跳投的概率为