2022-2023学年浙教版数学九年级上册1.4 二次函数的应用同步练习

试卷更新日期：2022-07-05 类型：同步测试

进入出卷网下载

一、单选题

1. 已知二次函数 $y = a x^{2} + b x + c$ 的图象交x轴于A(x₁ ， 0)，B(x₂ ， 0)两点，交y轴于点C(0，3)，若 $x_{1} + x_{2} = 4$ ，且△ABC的面积为3，则a+b（）

A、3 B、-5 C、-3 D、5

查看试题解析
2. 在求解方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 时，先在平面直角坐标系中画出函数 $y = a x^{2} + b x + c$ 的图象，观察图象与x轴的两个交点，这两个交点的横坐标可以看作是方程的近似解，分析右图中的信息，方程的近似解是（）

A、 $x_{1} = - 3$ ， $x_{2} = 2$ B、 $x_{1} = - 3$ ， $x_{2} = 3$ C、 $x_{1} = - 2$ ， $x_{2} = 2$ D、 $x_{1} = - 2$ ， $x_{2} = 3$

查看试题解析
3. 如图，二次函数y＝ax²+bx+c与反比例函数y＝ $\frac{k}{x}$ 的图象相交于点A（﹣1，y₁）、B（1，y₂）、C（3，y₃）三个点，则不等式ax²+bx+c＞ $\frac{k}{x}$ 的解集是（）

A、﹣1＜x＜0或1＜x＜3 B、x＜﹣1或1＜x＜3 C、﹣1＜x＜0或x＞3 D、﹣1＜x＜0或0＜x＜1

查看试题解析
4. 一次函数 $y = b x + a (b \neq 0)$ 与二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 在同一平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
5. 如图，已知抛物线 $y = a x^{2} + c$ 与直线 $y = k x + m$ 交于 $A (- 3 ， y_{1})$ ， $B (1 ， y_{2})$ 两点，则关于x的不等式 $a x^{2} + c \geq k x + m$ 的解集是（）

A、 $x \leq - 3$ 或 $x \geq 1$ B、 $x \leq - 1$ 或 $x \geq 3$ C、 $- 3 \leq x \leq 1$ D、 $- 1 \leq x \leq 3$

查看试题解析
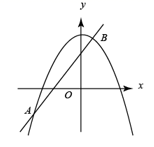6. 将二次函数 $y = - x^{2} + 2 x + 3$ 的图象在x轴上方的部分沿x轴翻折后，所得新函数的图象如图所示．当直线 $y = x + b$ 与新函数的图象恰有3个公共点时，b的值为（）

A、 $- \frac{21}{4}$ 或 $- 3$ B、 $- \frac{13}{4}$ 或 $- 3$ C、 $\frac{21}{4}$ 或 $- 3$ D、 $\frac{13}{4}$ 或 $- 3$

查看试题解析
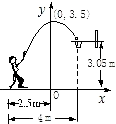
7. 如图，一个矩形的长比宽多3cm，矩形的面积是Scm² ．设矩形的宽为xcm，当x在一定范围内变化时，S随x的变化而变化，则S与x满足的函数关系是（）

A、S=4x+6 B、S=4x-6 C、S=x²+3x D、S=x²-3x

查看试题解析
8. 商店销售一种进价为50元/件的商品，售价为60元/件，每星期可卖出200件，若每件商品的售价上涨1元，则每星期就会少卖10件．每件商品的售价上涨x元（x正整数），每星期销售的利润为y元，则y与x的函数关系式为（）

A、y＝10（200﹣10x） B、y＝200（10+x） C、y＝10（200﹣10x）² D、y＝（10+x）（200﹣10x）

查看试题解析
9. 一人一盔安全守规，一人一带平安常在！某商店销售一批头盔，售价为每顶80元，每月可售出200顶．在“创建文明城市”期间，计划将头盔降价销售，经调查发现：每降价1元，每月可多售出20顶．已知头盔的进价为每顶50元，则该商店每月获得最大利润时，每顶头盔的售价为（）元．

A、60 B、65 C、70 D、75

查看试题解析
10. 一位运动员在离篮筐水平距离4m处起跳投篮，球运行路线可看作抛物线，当球离开运动员的水平距离为1m时，它与篮筐同高，球运行中的最大高度为3.5m，最后准确落入篮筐，已知篮筐到地面的距离为3.05m，该运动员投篮出手点距离地面的高度为（）

A、1.5m B、2m C、2.25m D、2.5m

查看试题解析

二、填空题

11. 如图是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的过程，它是一条经过A、M、C三点的抛物线．其中A点离地面1.4米，M点是足球运动过程中的最高点，离地面3.2米，离守门员的水平距离为6米，点C是球落地时的第一点．那么足球第一次落地点C距守门员的水平距离为米．

查看试题解析
12. 如图，若被击打的小球飞行高度 $h$ （单位： $m$ ）与飞行时间 $t$ （单位： $s$ ）之间具有的关系为 $h = 20 t - 5 t^{2}$ ，则小球从飞出到落地所用的时间为 $s$ ．

查看试题解析
13. 某件商品的销售利润y（元）与商品销售单价x（元）之间满足 $y = - x^{2} + 6 x - 7$ ，不考虑其他因素，销售一件该商品的最大利润为元．

查看试题解析
14. 某电商平台11月1日起开始销售一款新品牌手机，当月的日销售额y（万元）和销售时间第x天（1≤x≤30且x为整数）之间满足二次函数关系y=-（x-h）+k，根据市场调查可以确定在当月中旬日销售额达到最大值．

(1)、若第18天的销售额比第19天的销售额多5万元，则第天的日销售额最大；

(2)、若第18天后的日销售额呈下降趋势，则h的取值范围是

查看试题解析
15. 如图，已知抛物线 $y = - \frac{3}{16} (x + 4) (x - 4)$ 与 $x$ 轴交于 $A$ 、 $B$ 两点，与 $y$ 轴交于 $C$ 点， $⊙ C$ 的半径为2． $G$ 为 $⊙ C$ 上一动点， $P$ 为 $A G$ 的中点，则 $A G$ 的最小值为， $O P$ 的最大值为．

查看试题解析
16. 如图，在矩形 ABCD 中，AD＝3，点E是AD边上的动点，连结CE，以CE为边向右上方作正方形CEFG，过点F作 FH⊥AD，垂足为H，连结AF. 在整个变化过程中，△AEF 面积的最大值是．

查看试题解析
17. 如图，一次函数 $y = a x + b (a < 0 ， b > 0)$ 的图像与x轴，y轴分别相交于点A，点B，将它绕点O逆时针旋转90°后，与x轴相交于点C，我们将图像过点A，B，C的二次函数叫做与这个一次函数关联的二次函数．如果一次函数 $y = - k x + k (k > 0)$ 的关联二次函数是 $y = m x^{2} + 2 m x + c$ （ $m \neq 0$ ），那么这个一次函数的解析式为．

查看试题解析
18. 如图是二次函数y=-x²+bx+c的部分图象，若 $y \geq 0$ ，则x的取值范围是.

查看试题解析
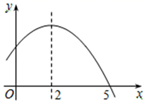19. 二次函数y＝ax²+bx+c（a≠0）的图象如图所示，则关于x的方程ax²+bx+c＝0（a≠0）的解为．

查看试题解析
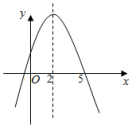20. 写出一组a，b的值，使二次函数y＝ax²+bx+2的图象与x轴有两个不同的交点，则a，b的值可以是a＝， b＝．

查看试题解析

三、解答题

21. 已知：二次函数y＝x²﹣2x﹣3．将y＝x²﹣2x﹣3用配方法化成y＝a（x﹣h）²+k的形式，并求此函数图象与x轴、y轴的交点坐标．

查看试题解析
22.
已知二次函数y=﹣x²+2x+m的部分图象如图所示，你能确定关于x的一元二次方程﹣x²+2x+m=0的解？

查看试题解析
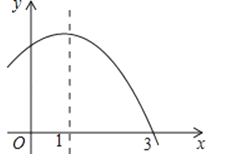23. 根据下列要求，解答相关问题．

(1)、请补全以下求不等式 $x^{2} - 2 x < 0$ 的解集的过程：
①构造函数，画出图象：根据不等式特征构造二次函数y= $x^{2} - 2 x$ ；并在下面的坐标系中（图1）画出二次函数y= $x^{2} - 2 x$ 的图象（只画出大致图象即可）；
②求得界点，标示所需：当 $y = 0$ 时，求得方程 $x^{2} - 2 x = 0$ 的解为；并用虚线标示出函数y= $x^{2} - 2 x$ 图象中 $y$ ＜0的部分；
③借助图象，写出解集：由所标示图象，可得不等式 $x^{2} - 2 x$ ＜0的解集为．

(2)、请你利用上面求不等式解集的过程，求不等式 $x^{2} - 2 x$ -3≥0的解集．

查看试题解析

四、综合题

24. 如图，已知直线y＝﹣2x+m与抛物线相交于A，B两点，且点A(1，4)为抛物线的顶点，点B在x轴上．

(1)、求抛物线的解析式；

(2)、若点P是y轴上一点，当∠APB＝90°时，求点P的坐标．

查看试题解析
25. 如图，用一段长36米的篱笆，围成一个矩形花圃，花圃的一边靠墙（墙足够长），设AB边的长为x米，矩形ABCD的面积为S平方米．

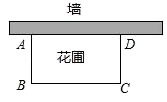(1)、求 $S$ 与 $x$ 之间的函数关系式，并写出自变量 $x$ 的取值范围；

(2)、当 $x$ 为何值时， $S$ 有最大值？并求出最大值．

查看试题解析
26. 如图，Rt△ABC中，∠C＝90°，AC＝6，BC＝8，动点P、Q分别从A、C两点同时出发，P点沿边AC向C以每秒3个单位长度的速度运动，Q点沿边BC向B以每秒4个单位长度的速度运动，当P、Q到达终点C、B时，运动停止，设运动时间为t（s）．

(1)、①当运动停止时，t的值为；
②设P、C之间的距离为y，则y与t满足关系（填“正比例函数”、“一次函数”或“二次函数”）；

(2)、设△PCQ的面积为S．
①求S的表达式（用含t的式子表示）；
②求当t为何值时，S取得最大值，这个最大值是多少？

查看试题解析
27. 如图，在平面直角坐标系中，直线 $A B ： y = k x + 3$ 与坐标轴交于A，B两点，经过点B的抛物线 $y = a x^{2} + b x$ 交直线 $A B$ 于点 $C (2 ， 2)$ ．

(1)、求该抛物线的解析式．

(2)、在直线 $A B$ 上方的抛物线上是否存在点P，使得 $S_{△ P A O} = S_{△ P B O}$ ，若存在请求出点P的坐标，若不存在请说明理由．

查看试题解析
28. 某公司对办公大楼一块墙面进行如图所示的图案设计.这个图案由四个全等的直角三角形和一个小正方形拼接而成的大正方形，设小正方形的边长 $m$ ，直角三角形较短边长 $n$ ，且 $n = 2 m - 4$ ，大正方形的面积为 $S$ .

(1)、求 $S$ 关于 $m$ 的函数关系式.

(2)、若小正方形边长不大于3，当大正方形面积最大时，求 $m$ 的值.

查看试题解析
29. 绿色生态农场生产并销售某种有机生态水果.经市场调查发现，该生态水果的周销售量y（千克）是销售单价x（元/千克）的一次函数.其销售单价、周销售量及周销售利润w（元）的对应值如表.请根据相关信息，解答下列问题：

销售单价x（元/千克）

40

50

周销售量y（千克）

180

160

周销售利润w（元）

1800

3200

(1)、这种有机生态水果的成本为元/千克；

(2)、求该生态水果的周销售量y（千克）与销售单价x（元/千克）之间的函数关系式；

(3)、若农场按销售单价不低于成本价，且不高于60元/千克销售，则销售单价定为多少，才能使销售该生态水果每周获得的利润w（元）最大？最大利润是多少？

查看试题解析
30. 524红薯富含膳食纤维，维生素（A，B，C，D，E）以及钾，铁等10余种微量元素，被营养学专家称为营养均衡的保健食品，深受广大消费者喜爱.某土特产批发店以30元/箱的价格进货.根据市场调查发现，批发价定位48元/箱时，每天可销售500箱，为保证市场占有率，决定降价销售，发现每箱降价1元，每天可增加销量50箱.

(1)、写出每天的利润 $w$ 与降价 $x$ 元的函数关系式；

(2)、当降价多少元时，每天可获得最大利润，为多少？

(3)、要使每天的利润为9750元，并让利于民，应降价多少元？

查看试题解析
31. 如图，一位运动员在距篮下4米处跳起投篮，球运行的路线是抛物线，当球运行的水平距离为2.5米时，达到最大高度3.5米，然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.

(1)、建立如图所示的直角坐标系，求抛物线的表达式；

(2)、该运动员身高1.8米，在这次跳投中，球在头顶上方0.25米处出手，问：球出手时，他跳离地面的高度是多少？

查看试题解析
32. 如图，一名男生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ．求：

(1)、铅球在行进中的最大高度；

(2)、该男生将铅球推出的距离是多少m？

查看试题解析

销售单价x（元/千克）	40	50
周销售量y（千克）	180	160
周销售利润w（元）	1800	3200

2022-2023学年浙教版数学九年级上册1.4 二次函数的应用 同步练习

一、单选题

二、填空题

三、解答题

四、综合题

2022-2023学年浙教版数学九年级上册1.4 二次函数的应用同步练习