2022-2023学年初数北师大版九年级上册第二章 一元二次方程 章末检测
试卷更新日期:2022-07-05 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 解一元二次方程最适宜的方法是( )A、直接开平方 B、公式法 C、因式分解法 D、配方法2. 下列关于 的方程:① ;② ;③ ;④ ;⑤ ;⑥ .其中一元二次方程有( )A、1个 B、2个 C、3个 D、4个3. 根据下列表格的对应值:可得方程x2+5x﹣3=0一个解x的范围是( )
x
0.00
0.25
0.50
0.75
1.00
x2+5x﹣3
-3.00
-1.69
-0.25
1.31
3.00
A、0<x<0.25 B、0.25<x<0.50 C、0.50<x<0.75 D、0.75<x<14. 用配方法解方程 x2 + 6x -1 = 0 时,配方结果正确的是( )A、(x - 3)2 = 10 B、(x - 3)2 = 8 C、(x + 3)2 = 8 D、(x + 3)2 = 105. 如图是小明在解方程 x2-2x-1= 0时的过程,他在解答过程中开始出错的步骤是( ) A、第①步 B、第②步 C、第③步 D、第④步6. 若 是某个一元一次方程的根,则这个一元二次方程可以是( )A、3x2+2x﹣1=0 B、2x2+4x﹣1=0 C、﹣x2﹣2x+3=0 D、3x2﹣2x﹣1=07. 将关于 的一元二次方程 变形为 ,就可以将 表示为关于 的一次多项式,从而达到“降次”的目的,又如 …,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知: ,且 ,则 的值为( )A、 B、 C、 D、8. 在正数范围内有一种运算“*”,其规则为 ,根据这个规则,方程 的解是 ( )A、 B、 C、 D、9. 若关于x的方程有两个实数根x1、x2 , 则的最小值为( )A、-2 B、 C、 D、10. 某小区原有一块长为30米,宽为20米的矩形康乐健身区域,现计划在这一场地四周(场内)筑一条宽度相等的健走步道,其步道面积为214平方米,设这条步道的宽度为x米,可以列出方程是( )
A、第①步 B、第②步 C、第③步 D、第④步6. 若 是某个一元一次方程的根,则这个一元二次方程可以是( )A、3x2+2x﹣1=0 B、2x2+4x﹣1=0 C、﹣x2﹣2x+3=0 D、3x2﹣2x﹣1=07. 将关于 的一元二次方程 变形为 ,就可以将 表示为关于 的一次多项式,从而达到“降次”的目的,又如 …,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知: ,且 ,则 的值为( )A、 B、 C、 D、8. 在正数范围内有一种运算“*”,其规则为 ,根据这个规则,方程 的解是 ( )A、 B、 C、 D、9. 若关于x的方程有两个实数根x1、x2 , 则的最小值为( )A、-2 B、 C、 D、10. 某小区原有一块长为30米,宽为20米的矩形康乐健身区域,现计划在这一场地四周(场内)筑一条宽度相等的健走步道,其步道面积为214平方米,设这条步道的宽度为x米,可以列出方程是( )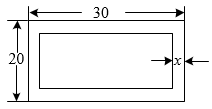 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 写出一个二次项系数为1,且有一个根为2的一元二次方程:.12. 我国南宋数学家杨辉所著《田亩比类乘除捷法》中记载了这样一道题:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步.”其大意为:一个矩形的面积为864平方步,宽比长少12步,问宽和长各多少步?设矩形的宽为x步,根据题意,可列方程为 .13. 若关于 的一元二次方程 通过配方法可以化成 的形式,则 的值可以是.(写出一个符合要求的 值).14. 对于两个不相等的实数a、b,我们规定:符号Max{a,b}表示a、b中的较大数,如:Max{﹣2,﹣4}=﹣2.按照这个规定,方程Max{x,﹣x}= 的解为.15. 三角形两边的长分别为3和6,第三边的长是方程x2﹣9x+18=0的根,则该三角形的周长为 .16. 已知关于x的一元二次方程 有两个实数根 , ,若 , 满足 ,则m的值为
三、解答题(共8题,共66分)
-
17. 用适当方法解下列一元二次方程:(1)、x2﹣6x=1;(2)、x2﹣4=3(x﹣2).18. 当m为何值时,关于x的方程 为一元二次方程,并求这个一元二次方程的解.19.(1)、根据要求,解答下列问题:
①方程 的解为;
②方程 的解为;
③方程 的解为;
(2)、根据以上方程特征及其解的特征,请猜想:①方程 的解为.
②关于x的方程的解为x1=1,x2=n;
(3)、请用配方法解方程 ,以验证猜想结论的正确性.20. 已知m,n是方程x2﹣2x﹣1=0的两个根,是否存在实数a使﹣(m+n)(7m2﹣14m+a)(3n2﹣6n﹣7)的值等于8?若存在,求出a的值;若不存在,请说明理由.21. 我们定义:如果关于的一元二次方程有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.(1)、请说明方程是倍根方程;(2)、若是倍根方程,则 , 具有怎样的关系?(3)、若一元二次方程是倍根方程,则 , , 的等量关系是(直接写出结果)22. 阅读资料:阅读材料,完成任务:材料 阿尔·花拉子密(约 780~约 850),著名数学家、天文学家、地理学家,是代数与算术的整理者,被誉为“代数之父”。
他用以下方法求得一元二次方程 x2+2x-35=0 的解:
将边长为 x 的正方形和边长为 1 的正方形,外加两个长方形,长为 x , 宽为 1,拼合在一起的面积是 x2+2×x×1+1×1,而由 x2+2x-35=0 变形得 x2+2x+1=35+1(如图所示),即右边边长为 x+1 的正方形面积为 36。
所以(x+1)2=36,则 x=5.
任务:请回答下列问题
(1)、上述求解过程中所用的方法是( )A、直接开平方法 B、公式法 C、配方法 D、因式分解法(2)、所用的数学思想方法是( )A、分类讨论思想 B、数形结合思想 C、转化思想 D、公理化思想(3)、运用上述方法构造出符合方程 x2+8x-9=0 的一个正根的正方形23. 2022年北京冬奥会吉祥物冰墩墩一开售,就深受大家的喜欢.某商店销售冰墩墩周边,每件冰墩墩周边进价60元,在销售过程中发现,当销售价为100元时,每天可售出30件,为庆祝冬奥会圆满落幕,该商店决定采取适当的降价措施,以扩大销售量增加利润,经市场调查发现,如果每件冰墩墩周边降价1元,平均可多售出3件.(1)、若每件冰墩墩周边降价5元,商家平均每天能盈利多少元?(2)、每件冰墩墩周边降价多少元时,能让利于顾客并且让商家平均每天能盈利1800元?24. 某牧场准备利用现成的一堵“7”字形的墙面(粗线A-B-C表示墙面)建饲养场,已知AB⊥BC,AB=3米,BC=15米,现计划用总长为38米的篱笆围建一个“日”字形的饲养场BDEF ,并在每个区域开一个宽2米的门,如图(细线表示篱笆,饲养场中间用篱笆GH隔开),点F可能在线段BC上,也可能在线段BC的延长线上. (1)、如图1,当点F在线段BC上时,
(1)、如图1,当点F在线段BC上时,①设EF的长为x米,则DE= ▲ 米;(用含 x的代数式表示)
②若围成的饲养场BDEF的面积为132平方米,求饲养场的宽EF的长;
(2)、如图2,当点F在线段BC延长线上,所围成的饲养场BDEF的面积能否为156平方米?如果能达到,求出EF的长;如果不能,请说明理由.