2022-2023学年初数北师大版九年级上册第一章 特殊平行四边形 章末检测
试卷更新日期：2022-07-05 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 绿丝带是颜色丝带的一种，被用来象征许多事物，例如环境保护、大麻和解放农业等，同时绿丝带也代表健康，使人对健康的人生与生命的活力充满无限希望．某班同学在“做环保护航者”的主题班会课上制作象征“健康快乐”的绿丝带（丝带的对边平行且宽度相同），如图所示，丝带重叠部分形成的图形是（ ）
A、矩形 B、菱形 C、正方形 D、等腰梯形2. 如图，在菱形ABCD中，对角线AC与BD相交于点O，且AC=6，DB=8，AE⊥BC于点E，则AE=（ ）
A、6 B、8 C、 D、3. 如图，在菱形ABCD中，E，F分别是AB，AC的中点，如果EF=2，那么菱形ABCD周长是（ ）
A、4 B、8 C、12 D、164. 已知矩形ABCD的周长为20cm，两条对角线AC，BD相交于点O，过点O作AC的垂线EF，分别交两边AD，BC于E，F（不与顶点重合），则以下关于△CDE与△ABF判断完全正确的一项为（ ）A、△CDE与△ABF的周长都等于10cm，但面积不一定相等 B、△CDE与△ABF全等，且周长都为10cm C、△CDE与△ABF全等，且周长都为5cm D、△CDE与△ABF全等，但它们的周长和面积都不能确定5. 下图是文易同学答的试卷，文易同学应得（ ）
A、40分 B、60分 C、80分 D、100分6. 如图，四边形ABCD是菱形，对角线AC ， BD交于点O ， E是边AD的中点，过点E作EF⊥BD ， EG⊥AC ， 点F ， G为垂足，若AC=10，BD=24，则FG的长为（ ）
A、 B、 C、 D、7. 已知四边形ABCD是平行四边形，下列结论：①当AB＝BC时，它是菱形；②当AC⊥BD时，它是菱形；③当∠ABC＝90°时，它是矩形；④当AC＝BD时，它是正方形，其中不正确的有（ ）A、1个 B、2个 C、3个 D、4个8. 如图，正方形ABCD的对角线相交于点O，以点O为顶点的正方形OEGF的两边OE，OF分别交正方形ABCD的两边AB，BC于点M，N，记 的面积为 ， 的面积为 ，若正方形的边长 ， ，则 的大小为（ ）
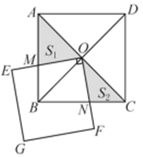A、6 B、7 C、8 D、99. 如图，菱形 ABCD 对角线交点与坐标原点 O 重合，点 A（-2，5） ，则点C的坐标为（ ）
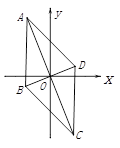A、 B、 C、 D、10. 如图，将图1中的菱形纸片沿对角线剪成4个直角三角形，拼成如图2的四边形 （相邻纸片之间不重叠，无缝隙）.若四边形 的面积为13，中间空白处的四边形 的面积为1，直角三角形的两条直角边分别为 和 ，则 （ ）
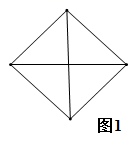
A、12 B、13 C、24 D、25二、填空题（每题4分，共24分）
-
11. 如图，菱形ABCD中，∠A=60°，BD=3，则菱形ABCD的周长是 ．
12. 已知菱形的两条对角线的长分别是10㎝和24㎝，那么菱形的每条边长是.13. 矩形ABCD的对角线AC和BD相交于点O，∠ACB=40°，则∠AOB=°．14. 如图，点O是菱形ABCD对角线的交点，DEAC，CEBD，连接OE，设AC＝12，BD＝16，则OE的长为 ．
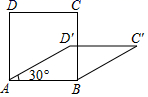
15. 四边形具有不稳定性，对于四条边长确定的四边形，当内角度数发生变化时，其形状也会随之改变．如图，改变正方形ABCD的内角度数，正方形ABCD变为菱形 ，若 ，且菱形 的面积为16，则正方形ABCD的面积为 ．
16. 如图，已知正方形ABCD的边长为2，在BC的延长线上取点B1 ， 使∠CB1D＝60°，分别过点D，B1作DB1 ， BC的垂线，两垂线交于点A1 ， 再以A1B1为边向右侧作正方形A1B1C1D1；在BC1的延长线上取点B2 ， 使∠C1B2D1＝60°，分别过点D1 ， B2作D1B2 ， BC1的垂线，两垂线交于点A2 ， 再以A2B2为边向右侧作正方形A2B2C2D2；……，按此规律继续作下去，则正方形A2022B2022C2022D2022的面积为 ．
三、解答题（共8题，共66分）
-
17. 如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA边上的中点，阅读下列材料，
(1)、连接AC、BD，由三角形中位线的性质定理可证四边形EFGH是；(2)、对角线AC、BD满足条件时，四边形EFGH是矩形；(3)、对角线AC、BD满足条件时，四边形EFGH是菱形；(4)、对角线AC、BD满足条件时，四边形EFGH是正方形．18. 如图是由边长为1的小正方形构成的 的网格，点A，B均在格点上.
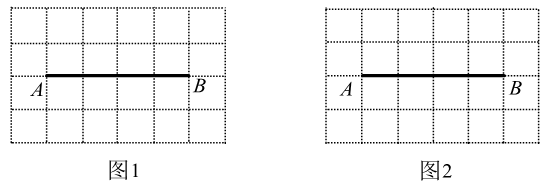(1)、在图1中画出以 为边且周长为无理数的 ，且点C和点D均在格点上（画出一个即可）.(2)、在图2中画出以 为对角线的正方形 ，且点E和点F均在格点上.19. 已知：在菱形 中，点E，O，F分别为AB，AC，AD的中点，连接 ， .求证： ；
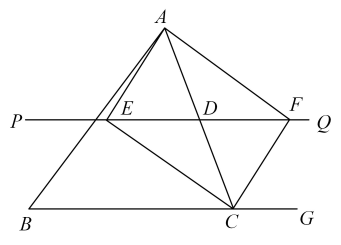
20. 如图，△ABC中，点D是边AC的中点，过D作直线PQ∥BC，∠BCA的平分线交直线PQ于点E，点G是△ABC的边BC延长线上的点，∠ACG的平分线交直线PQ于点F．求证：四边形AECF是矩形．
21. 已知平行四边形ABCD，AC是它的对角线．
(1)、用尺规作AC的垂直平分线EF，垂足为O，EF交AB于点E，交CD于点F（不写作法，但要保留痕迹）；(2)、连接AF、CE，求证：四边形AFCE是菱形；22. 如图，菱形ABCD的对角线AC、BD相交于点O ， 过点B作BE∥AC ， 且BE＝ AC ， 连接EC ．
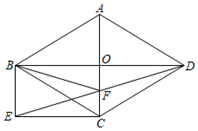(1)、求证：四边形BECO是矩形；(2)、连接ED交AC于点F ， 连接BF ， 若AC＝12，AB＝10，求BF的长．23. 如图，点E是平行四边形ABCD对角线AC上一点，点F在BE延长线上，且EF＝BE，EF与CD交于点G．
(1)、求证：DF∥AC；(2)、连接DE、CF，若2AB＝BF，且G恰好是CD的中点，求证：四边形CFDE是矩形；(3)、在（2）的条件下，若四边形CFDE是正方形，且BC＝80，求AB的长．24. 我们把有一组对角都是直角的四边形，叫做“对直四边形”.例如图1，四边形 中， ，那么四边形 就是对直四边形.
(1)、在已经学过的“①平行四边形；②菱形；③矩形；④正方形”中，一定是对直四边形是 ；（填序号）(2)、如图2，四边形 是对直四边形，若 ， ， ， ， ，求四边形 的面积；(3)、如图3，在正方形 中，点 ， ， 分别从点 ， ， 同时出发，并分别以每秒1，1，2个单位长度的速度，分别沿正方形的边 ， ， 方向运动（保持 ，再分别过点 ， 作 ， 的垂线交于点 ，连结 ， .求证：四边形 为对直四边形.