2022-2023学年初数北师大版九年级上册1.3正方形的性质与判定 同步训练
试卷更新日期:2022-07-05 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 正方形的一条对角线之长为4,则此正方形的面积是( )A、16 B、4 C、8 D、82. 下列条件中,能判定四边形是正方形的是( )A、对角线相等的平行四边形 B、对角线互相平分且垂直的四边形 C、对角线互相垂直且相等的四边形 D、对角线相等且互相垂直的平行四边形3. 如图,在 的正方形网格中,每个小正方形的边长均为1,四边形 的周长记为c,若 (a为正整数),则a的值为( )
 A、4 B、5 C、6 D、74. 如图,在矩形ABCD中,对角线AC,BD交于点O,下列条件:①AC⊥BD,②AB=BC,③∠ACB=45°,④OA=OB.上述条件能使矩形ABCD是正方形的是( )
A、4 B、5 C、6 D、74. 如图,在矩形ABCD中,对角线AC,BD交于点O,下列条件:①AC⊥BD,②AB=BC,③∠ACB=45°,④OA=OB.上述条件能使矩形ABCD是正方形的是( ) A、①②③④ B、①②③ C、②③④ D、①③④5. 如图,四边形ABCD是平行四边形,从下列条件:①AB=BC , ②∠ABC=90°,③AC=BD , ④AC⊥BD中,选出其中两个,使平行四边形ABCD变为正方形.下面组合错误的是( )
A、①②③④ B、①②③ C、②③④ D、①③④5. 如图,四边形ABCD是平行四边形,从下列条件:①AB=BC , ②∠ABC=90°,③AC=BD , ④AC⊥BD中,选出其中两个,使平行四边形ABCD变为正方形.下面组合错误的是( ) A、①② B、①③ C、③④ D、①④6. 下列命题正确的是( )A、有一组邻边相等的平行四边形是正方形 B、有一个角是直角的平行四边形是正方形 C、对角线相等的菱形是正方形 D、对角线互相平分的矩形是正方形7. 正方形具有而矩形不一定有的性质是( )A、对角线互相垂直 B、对角线相等 C、对角互补 D、四个角相等8. 如图, ,其中 , , ,M为BC中点,EF过点M交AC、BD于点E、F , 连接BE、CF , 则下列结论错误的是( ).
A、①② B、①③ C、③④ D、①④6. 下列命题正确的是( )A、有一组邻边相等的平行四边形是正方形 B、有一个角是直角的平行四边形是正方形 C、对角线相等的菱形是正方形 D、对角线互相平分的矩形是正方形7. 正方形具有而矩形不一定有的性质是( )A、对角线互相垂直 B、对角线相等 C、对角互补 D、四个角相等8. 如图, ,其中 , , ,M为BC中点,EF过点M交AC、BD于点E、F , 连接BE、CF , 则下列结论错误的是( ). A、四边形BECF为平行四边形 B、当 时,四边形BECF为矩形 C、当 时,四边形BECF为菱形 D、四边形BECF不可能为正方形9. 如图四边形ABCD是正方形,点E、F分别在线段BC、DC上,∠BAE=30°.若线段AE绕点A逆时针旋转后与线段AF重合,则旋转的角度是( )
A、四边形BECF为平行四边形 B、当 时,四边形BECF为矩形 C、当 时,四边形BECF为菱形 D、四边形BECF不可能为正方形9. 如图四边形ABCD是正方形,点E、F分别在线段BC、DC上,∠BAE=30°.若线段AE绕点A逆时针旋转后与线段AF重合,则旋转的角度是( ) A、30° B、45° C、60° D、90°10. 如图,在平行四边形 中, , , , 是对角线 上的动点,且 , , 分别是边 ,边 上的动点.下列四种说法:
A、30° B、45° C、60° D、90°10. 如图,在平行四边形 中, , , , 是对角线 上的动点,且 , , 分别是边 ,边 上的动点.下列四种说法:①存在无数个平行四边形 ;
②存在无数个矩形 ;
③存在无数个菱形 ;
④存在无数个正方形 .其中正确的个数是( )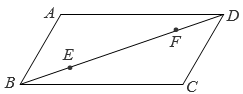 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(每题3分,共18分)
-
11. 已知在四边形ABCD中, ,若使四边形ABCD是正方形,则还需加上一个条件: .12. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.
 13. 如图,在正方形ABCD中,AB=2,取AD的中点E,连接EB,延长DA至F,使EF=EB,以线段AF为边作正方形AFGH,点H在线段AB上,则的值是 .
13. 如图,在正方形ABCD中,AB=2,取AD的中点E,连接EB,延长DA至F,使EF=EB,以线段AF为边作正方形AFGH,点H在线段AB上,则的值是 . 14. 如图,四边形和四边形都是边长为4的正方形,点O是正方形对角线的交点,正方形绕点O旋转过程中分别交 , 于点E,F,则四边形的面积为 .
14. 如图,四边形和四边形都是边长为4的正方形,点O是正方形对角线的交点,正方形绕点O旋转过程中分别交 , 于点E,F,则四边形的面积为 . 15. 如图,连接四边形ABCD各边的中点,得到四边形EFGH,还要添加 , 才能保证四边形EFGH是正方形.
15. 如图,连接四边形ABCD各边的中点,得到四边形EFGH,还要添加 , 才能保证四边形EFGH是正方形. 16. 如图,在中, , , 分别以的三边为边向外作三个正方形 , , , 连接.过点作的垂线 , 垂足为 , 分别交 , 于点 , .若 , , 则四边形的面积是.
16. 如图,在中, , , 分别以的三边为边向外作三个正方形 , , , 连接.过点作的垂线 , 垂足为 , 分别交 , 于点 , .若 , , 则四边形的面积是.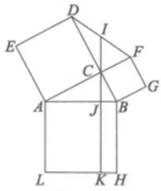
三、解答题
-
17. 如图为正方形网格,每个小正方形的边长均为1,各个小正方形的顶点叫做格点,请在下面的网格中按要求分别画图,使得每个图形的顶点均在格点上.
 (1)、在图中画一个以 为一边的菱形 ,且菱形 的面积等于20.(2)、在图中画一个以 为对角线的正方形 ,并直接写出正方形 的面积.18. 如图,四边形 是正方形,对角线 、 相交于点F, , .求证:四边形 是正方形.
(1)、在图中画一个以 为一边的菱形 ,且菱形 的面积等于20.(2)、在图中画一个以 为对角线的正方形 ,并直接写出正方形 的面积.18. 如图,四边形 是正方形,对角线 、 相交于点F, , .求证:四边形 是正方形.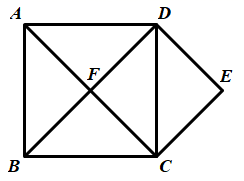 19. 如图,已知在矩形 中, , , , 分别是四个内角的平分线, , 相交于点 , , 相交于点 求证:四边形 是正方形.
19. 如图,已知在矩形 中, , , , 分别是四个内角的平分线, , 相交于点 , , 相交于点 求证:四边形 是正方形. 20. 如图,A、B、C三点在同一条直线上,AB=2BC,分别以AB,BC为边做正方形ABEF和正方形BCMN,联结FN,EC. 求证:FN=EC.
20. 如图,A、B、C三点在同一条直线上,AB=2BC,分别以AB,BC为边做正方形ABEF和正方形BCMN,联结FN,EC. 求证:FN=EC. 21. 如图,在菱形中,对角线 , 相交于点 , 点 , 在对角线上,且 , .
21. 如图,在菱形中,对角线 , 相交于点 , 点 , 在对角线上,且 , .求证:四边形是正方形.
 22. 如图,已知在▱ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且EA=EC.
22. 如图,已知在▱ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且EA=EC. (1)、求证:四边形ABCD是菱形;(2)、若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.23. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE.
(1)、求证:四边形ABCD是菱形;(2)、若∠DAC=∠EAD+∠AED,求证:四边形ABCD是正方形.23. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE. (1)、求证:CE=AD;(2)、当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)24. 问题背景:在课外小组活动中,“创新小组”对“正方形旋转”问题进行了探究,如图①,边长为6的正方形ABCD的对角线相交于点E,分别延长EA到点F,EB到点H,使AF=BH,再以EF,EH为邻边做正方形EFGH,连接AH,DF;
(1)、求证:CE=AD;(2)、当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)24. 问题背景:在课外小组活动中,“创新小组”对“正方形旋转”问题进行了探究,如图①,边长为6的正方形ABCD的对角线相交于点E,分别延长EA到点F,EB到点H,使AF=BH,再以EF,EH为邻边做正方形EFGH,连接AH,DF; (1)、解决问题:AH与DF之间的数量关系是 , 位置关系是;(2)、深入研究:如图②正方形EFGH固定不动,将正方形ABCD绕点E顺时针方向旋转α°,判断AH与DF的关系,并证明:(3)、拓展延伸:如图③,在正方形ABCD旋转过程中(0 °<α<90 °),AB,BC分别交EF,EH于点M,N,连接MN,EC.
(1)、解决问题:AH与DF之间的数量关系是 , 位置关系是;(2)、深入研究:如图②正方形EFGH固定不动,将正方形ABCD绕点E顺时针方向旋转α°,判断AH与DF的关系,并证明:(3)、拓展延伸:如图③,在正方形ABCD旋转过程中(0 °<α<90 °),AB,BC分别交EF,EH于点M,N,连接MN,EC.①当AM=2时,直接写出S△BMN+S△CEN的值;
②若α=45°,在不添加字母的情况下,请你在图中再找两个点,和点M,N所围成的四边形是特殊四边形,直接写出这个特殊四边形.(写两个,不需要证明,需要指明是什么特殊四边形)