2022-2023学年初数北师大版九年级上册1.1菱形的判定与性质 同步训练
试卷更新日期：2022-07-04 类型：同步测试
一、单选题（每题2分，共20分）
-
1. 关于菱形的性质，以下说法错误的是（ ）A、四条边相等 B、对角线相等 C、对角线互相垂直 D、是轴对称图形2. 如图，菱形OABC的边OA在平面直角坐标系中的x轴上， ， ，则点C的坐标为（ ）
A、 B、 C、 D、3. 小明用四根长度相同的木条制作了能够活动的菱形学具，他先活动学具成为图1所示菱形，并测得∠B＝60°，对角线AC＝10cm，接着活动学具成为图2所示正方形，则图2中对角线AC的长为（ ）
A、10cm B、20cm C、30cm D、cm4. 如图，在菱形ABCD中，对角线AC与BD相交于点O，且AC＝12，BD＝16，则菱形的高AE为（ ）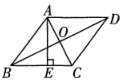
A、9.6 B、4.8 C、10 D、55. 菱形ABCD的周长是8cm，∠ABC＝60°，那么这个菱形的对角线BD的长是（ ）A、cm B、2cm C、1cm D、2cm6. 如图，下列条件能使平行四边形ABCD是菱形的为（ ）①AC⊥BD；②∠BAD=90°；③AB=BC；④AC=BD ．
A、①③ B、②③ C、③④ D、①7. 小明制作了5张卡片，上面分别写了一个条件：① ；② ；③ ；④ ，⑤ ．从中随机抽取一张卡片，能判定 是菱形的概率为（ ）A、 B、 C、 D、8. 如图，是一张平行四边形纸片ABCD，要求利用所学知识作出一个菱形，甲、乙两位同学的作法分别如下：甲：连接AC，作AC的中垂线交AD、BC于E、F，则四边形AFCE是菱形.
乙：分别作 ∠A 与 ∠B 的平分线AE、BF，分别交BC于点E，交AD于点F，则四边形ABEF是菱形.
对于甲、乙两人的作法，可判断（ ）
A、甲正确，乙错误 B、甲错误，乙正确 C、甲、乙均正确 D、甲、乙均错误9. 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若AE＝6，AB＝5，则BF的长为（ ）
A、5 B、6 C、8 D、1210. 下列说法中错误的是（ ）A、四边相等的四边形是菱形 B、菱形的对角线长度等于边长 C、一组邻边相等的平行四边形是菱形 D、对角线互相垂直平分的四边形是菱形二、填空题（每题3分，共18分）
-
11. 如图，在菱形ABCD中，已知AB＝5，AC＝6，那么菱形ABCD的面积为 ．
12. 如图 ， 已知菱形ABCD，E、F分别为 △ABD和△CBD的重心， 如果边AB=5， 对角线BD=6， 那么EF的长为 ．
13. 如图，菱形ABCD的对角线AC，BD相交于点O，E为DC的中点，若 ， 则菱形的周长为 ．
14. 如图，在四边形 中， ，E，F，G，H分别是 ， ， ， 的中点，要使四边形 是菱形，四边形 还应满足的一个条件是.
15. 如图，在条件：①∠COA＝∠AOD＝60°；②AC＝AD＝OA；③点E分别是AO、CD的中点；④OA⊥CD且∠ACO＝60°中，能推出四边形OCAD是菱形的条件有个．
16. 如图，两条宽都为4cm的纸条交叉成45°角重叠在一起，则重叠四边形的面积为 cm2 ．
三、解答题（共8题，共62分）
-
17. 如图，在菱形ABCD中，点E ， F是对角线BD的三等分点，连接AE ， EC ， CF和FA ． 已知AB＝2 ，四边形AECF是正方形，求BD的长．
18. 如图，在中， ， 是的中线，点E是的中点，过点C作CF∥AB交的延长线于点F，连接 ． 请判断四边形的形状，并加以证明．
19. 已知线段AC
(1)、尺规作图：作菱形ABCD，使AC是菱形的一条对角线（保留作图痕迹，不要求写作法）；(2)、若AC＝8，BD＝6，求菱形的边长．20. 如图，△ABC中，AB＝AC＝2，∠BAC＝45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE，CF相交于点D．
(1)、求证：BE＝CF；(2)、当四边形ACDE为菱形时，求BD的长．21. 如图，在△ABC中，∠ACB＝30°，将绕点C顺时针旋转60°得到△DEC ，连接AE．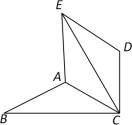
(1)、求证：AB=AE；(2)、若AB=AC，试判断四边形ACDE的形状，并说明理由．22. 在Rt△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕点B逆时针旋转一个角度α后得到△DBE，点A，C的对应点分别为点D，E．
(1)、如图1，若点D恰好落在边BC的延长线上，连接CE，求∠DEC的度数．(2)、如图2，若α＝60°，F为BD的中点，连接CD，CF，EF，请判断四边形CDEF是什么特殊的四边形，并说明理由．
