2022-2023学年浙教版数学八年级上册2.7 探索勾股定理同步练习

试卷更新日期：2022-07-04 类型：同步测试

进入出卷网下载

一、单选题

1. 下列各组数中，以它们为边长的线段能构成直角三角形的是（）

A、1，2，3 B、1， $\sqrt{2}$ ， $\sqrt{3}$ C、4，5，6 D、12，15，20

查看试题解析
2. 如图，以 $R t △ A B C$ 的三边为直角边分别向外作等腰直角三角形.若 $A B = \sqrt{3}$ ，则图中阴影部分的面积为（　　）

A、3 B、 $\frac{9}{2}$ C、 $3 \sqrt{2}$ D、 $3 \sqrt{5}$

查看试题解析
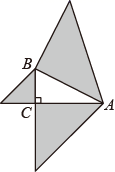3. 在 $R t Δ A B C$ 中， $∠ B = 90 °$ ， $A B = B C = 2$ ， $A C = a$ .下列关于a的四种说法：①a是无理数；②a可以用数轴上的一个点来表示；③a是8的算术平方根；④ $3 < a < 4$ .其中，所有正确的说法的序号是（）

A、①②④ B、②③④ C、①②③ D、①③④

查看试题解析
4. 如图，已知钓鱼竿 $A C$ 的长为 $10 m$ ，露在水面上的鱼线 $B C$ 长为 $6 m$ ，某钓鱼者想看看鱼钩上的情况，把鱼竿 $A C$ 转动到 $A C^{'}$ 的位置，此时露在水面上的鱼线 $B^{'} C^{'}$ 为 $8 m$ ，则 $B B^{'}$ 的长为（）

A、 $1 m$ B、 $2 m$ C、 $3 m$ D、 $4 m$

查看试题解析
5. 有一个边长为1的正方形，以它的一条边为斜边，向外作一个直角三角形，再分别以直角三角形的两条直角边为边，向外各作一个正方形，称为第一次“生长”（如图1）；再分别以这两个正方形的边为斜边，向外各自作一个直角三角形，然后分别以这两个直角三角形的直角边为边，向外各作一个正方形，称为第二次“生长”（如图2）……如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是（）

A、1 B、2020 C、2021 D、2022

查看试题解析
6. 已知△ABC中，∠A、∠B、∠C所对的边分别是a、b、c，满足下列条件的三角形中，不能判定△ABC为直角三角形是的（）

A、∠A：∠B：∠C＝3：4：5 B、∠A＝∠C﹣∠B C、a：b：c＝5：12：13 D、∠A：∠B：∠C＝1：2：3

查看试题解析
7. 如图，某超市为了吸引顾客，在超市门口离地高4.5m的墙上，装有一个由传感器控制的门铃A，如①图所示，人只要移至该门铃5m及5m以内时，门铃就会自动发出语音“欢迎光临”.如②图所示，一个身高1.5m的学生走到D处，门铃恰好自动响起，则BD的长为（）

A、3米 B、4米 C、5米 D、7米

查看试题解析
8. 有长为5cm，12cm的两根木条，现想找一根木条和这两根木条首尾顺次相连组成直角三角形，则下列木条长度适合的是（）

A、10cm B、13cm C、18cm D、20cm

查看试题解析
9. 如图，在数轴上点B表示的数为1，在点B的右侧作一个边长为1的正方形BACD，将对角线BC绕点B逆时针转动，使对角线的另一端落在数轴负半轴的点M处，则点M表示的数是（）

A、 $\sqrt{2}$ B、 $\sqrt{2}$ +1 C、1﹣ $\sqrt{2}$ D、﹣ $\sqrt{2}$

查看试题解析
10. 如图，在Rt△ABC中，∠ACB是直角，点D是AB边上的中点，下列成立的有（）
①∠A+∠B=90° ②AC²+BC²=AB² ③2CD=AB ④∠B= 30°

A、①②④ B、①③ C、②④ D、①②③

查看试题解析

二、填空题

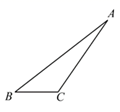
11. 直角三角形的两条边长分别为3cm、4cm，则这个直角三角形的斜边长为cm.

查看试题解析
12. 如图，在 $△$ ABC中，AB＝20，AC＝15，BC＝7，则点A到BC的距离是.

查看试题解析
13. 如图所示的长方体中，长AB＝5cm，宽BC＝3cm，高CD＝6cm，一只蚂蚁从顶点A处沿长方体的表面爬行到点D处，它爬行的最短距离为.

查看试题解析
14. 根据教材第65页“思考”栏目可以得到这样一个结论：如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，则AB＝2BC.请在这一结论的基础上继续思考：若AC＝2，点D是AB边上的动点，则CD+ $\frac{1}{2}$ AD的最小值为.

查看试题解析
15. 如图，等腰△BAC中，∠BAC＝120°，BC＝6，P为射线BA上的动点，M为BC上一动点，则PM+CP的最小值为．

查看试题解析
16. 如图，△ABC中，AB＝AC＝13，BC＝24，点D在BC上（BD＞CD），△AED与△ACD关于直线AD轴对称，点C的对称点是点E，AE交BC于点F，连结BE，CE.当DE⊥BC时，∠ADE的度数为， CE的长为 .

查看试题解析
17. 三角形的三边长分别为3，4，5，则最长边上的高为 .

查看试题解析
18. 如图所示，已知直线m∥n，且这两条平行线间的距离为5个单位长度，点P为直线n上一定点，以P为圆心、大于5个单位长度为半径画弧，交直线m于A、B两点.再分别以点A、B为圆心、大于 $\frac{1}{2}$ AB长为半径画弧，两弧交于点Q，作直线PQ，交直线m于点O，点H为射线OB上一动点，作点O关于直线PH的对称点O'，当点O'到直线n的距离为4个单位时，线段PH的长度为.

查看试题解析
19. 如图， $O A_{1} = A_{1} A_{2} = A_{2} A_{3} = A_{3} A_{4} = A_{4} A_{5} = 1$ ， $∠ O A_{1} A_{2} = ∠ O A_{2} A_{3} = ∠ O A_{3} A_{4} = ∠ O A_{4} A_{5} = 90 °$ ，则 $O A_{5}$ 的长是.

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， AB的垂直平分线交AB、AC于点D，E，若 $A C = 8$ ， $B D = 5$ ，则 $△ A D E$ 的面积是.

查看试题解析

三、解答题

21. 如图，在△ABC中，AD平分∠BAC.AB=AC=3，AD=2，求BC的长.

查看试题解析
22. 如图，△ABC中，∠ABC＝45°，F是高AD和高BE的交点，AC＝ $\sqrt{5}$ ， BD＝2．求线段DF的长度．

查看试题解析
23. 如图，在△ABC中，∠B＝45°，∠C＝30°，边AC的垂直平分线分别交边BC、AC于点D、E，DC＝6．求AB的长．

查看试题解析
24. 在甲村至乙村的公路旁有一块山地正在开发，现有一C处需要爆破．已知点C与公路上的停靠站A的距离为500米，与公路上另一停靠站B的距离为1200米，且CA⊥CB，如图，为了安全起见，爆破点C周围半径400米范围内不得进入．问在进行爆破时，公路AB段是否有危险，是否需要暂时封锁？请通过计算进行说明．

查看试题解析
25. 数学课上，老师出示了一个题：如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 5$ ， $A B = 13$ ， $∠ C A B$ 的平分线交CB于点D，求CD的长．
晓涵同学思索了一会儿，考虑到角平分线所在直线是角的对称轴这一特点，于是构造了一对全等三角形，解决了这个问题．请你在晓涵同学的启发下（或者独立思考后有自己的想法），解答这道题．

查看试题解析

四、综合题

26. 如图所示， $△ A B C$ 中， $B A = B C$ ， $C O ⊥ A B$ 于点 $O$ ， $A O = 4$ ， $B O = 6$ ．

(1)、求 $B C$ ， $A C$ 的长．

(2)、若点 $D$ 是射线 $O B$ 上的一个动点，作 $D E ⊥ A C$ 于点 $E$ ，连结 $O E$ ．
①当点 $D$ 在线段 $O B$ 上时，若 $△ A O E$ 是以 $A O$ 为腰的等腰三角形，请求出所有符合条件的 $O D$ 的长．

②设 $D E$ 交直线 $B C$ 于点 $F$ ，连结 $O F$ ， $C D$ ，若 $S_{△ O B F} ： S_{△ O C F} = 1 ： 4$ ，则 $C D$ 的长为多少？（直接写出结果）．

查看试题解析
27. 2021年10月10日是辛亥革命110周年纪念日．为进一步弘扬辛亥革命中体现的中华民族的伟大革命精神，社区开展了系列纪念活动．如图，有一块四边形空地，社区计划将其布置成展区，陈列有关辛亥革命的历史图片．现测得 $A B = A D = 26 m$ ， $B C = 16 m$ ， $C D = 12 m$ ，且 $B D = 20 m$ ．

(1)、试说明 $∠ B C D = 90 °$ ；

(2)、求四边形展区（阴影部分）的面积．

查看试题解析
28. 已知△ABC的三边a＝m²﹣1（m＞1），b＝2m ，c＝m²+1．

(1)、求证：△ABC是直角三角形．

(2)、利用第（1）题的结论，写出两个直角三角形的边长，要求它们的边长均为正整数．

查看试题解析
29. 如图，在 $△ A B C$ 中， $∠ A B C = 45 °$ ， $C D ⊥ A B$ ， $B E ⊥ A C$ ，CD与BE相交于点F.

(1)、求证： $△ A C D ≌ △ F B D$ ；

(2)、若 $A D = 3$ ， $B F = 5$ ，求 $△ A B C$ 的面积.

查看试题解析
30. 如图，在 $△ A B C$ 中， $A B = A C = 4$ ， $∠ B A C = 120 °$ .

(1)、求BC的长.

(2)、在线段BC上取点M，使 $B M = B A$ ，求 $△ A C M$ 的面积.

查看试题解析

2022-2023学年浙教版数学八年级上册2.7 探索勾股定理 同步练习

一、单选题

二、填空题

三、解答题

四、综合题

2022-2023学年浙教版数学八年级上册2.7 探索勾股定理同步练习