2022-2023学年浙教版数学八年级上册2.6 直角三角形 同步练习
试卷更新日期:2022-07-04 类型:同步测试
一、单选题
-
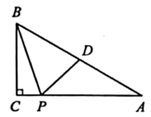
1. 如图,在中, , , 点D为边AB的中点,点P在边AC上,则周长的最小值等于( ).
 A、 B、 C、 D、2. 如图,为的角平分线, , , 点P,C分别为射线 , 上的动点,则的最小值是( )
A、 B、 C、 D、2. 如图,为的角平分线, , , 点P,C分别为射线 , 上的动点,则的最小值是( ) A、3 B、4 C、5 D、63. 已知:如图,在ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E.若∠CAB=30°,AB=6,则DE+DB的值为( )
A、3 B、4 C、5 D、63. 已知:如图,在ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E.若∠CAB=30°,AB=6,则DE+DB的值为( ) A、2 B、3 C、4 D、54. 如图所示,在直角三角形ACB中,已知∠ACB=90°,点E是AB的中点,且 , DE交AC的延长线于点D、交BC于点F,若∠D=30°,EF=2,则DF的长是( )
A、2 B、3 C、4 D、54. 如图所示,在直角三角形ACB中,已知∠ACB=90°,点E是AB的中点,且 , DE交AC的延长线于点D、交BC于点F,若∠D=30°,EF=2,则DF的长是( ) A、5 B、4 C、3 D、25. 如图,已知是平分线上的一点, , , 是的中点, , 如果是上一个动点,则的最小值为( )
A、5 B、4 C、3 D、25. 如图,已知是平分线上的一点, , , 是的中点, , 如果是上一个动点,则的最小值为( )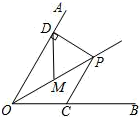 A、 B、 C、 D、6. 下列命题中,是真命题的是( )A、对应角相等的两个三角形是全等三角形 B、三个内角之比为3∶4∶5的三角形是直角三角形 C、平面直角坐标系中,点的横坐标是点到x轴的距离 D、角平分线上的点到角两边的距离相等7. 如图,在 中, , ,D为 的中点,P为 上一点,E为 延长线上一点,且 有下列结论:① ;② 为等边三角形;③ ;④ 其中正确的结论是( )
A、 B、 C、 D、6. 下列命题中,是真命题的是( )A、对应角相等的两个三角形是全等三角形 B、三个内角之比为3∶4∶5的三角形是直角三角形 C、平面直角坐标系中,点的横坐标是点到x轴的距离 D、角平分线上的点到角两边的距离相等7. 如图,在 中, , ,D为 的中点,P为 上一点,E为 延长线上一点,且 有下列结论:① ;② 为等边三角形;③ ;④ 其中正确的结论是( ) A、①②③④ B、①② C、①②④ D、③④8. 如图, 中, , , 平分 ,若 ,则点D到线段 的距离等于( )
A、①②③④ B、①② C、①②④ D、③④8. 如图, 中, , , 平分 ,若 ,则点D到线段 的距离等于( ) A、6 B、5 C、8 D、109. 如图,AE、AD分别是△ABC的高和角平分线,∠B=36°,∠C=76°,则∠DAE的度数为( )
A、6 B、5 C、8 D、109. 如图,AE、AD分别是△ABC的高和角平分线,∠B=36°,∠C=76°,则∠DAE的度数为( ) A、40° B、20° C、18° D、38°10. 如图,在等腰△ABC中,点M,N都在BC边上,∠BAC=120°,若ME⊥AB于点E,NF⊥AC于点F,点E,F分别为AB,AC的中点,且EM=2.则BC的长为( )
A、40° B、20° C、18° D、38°10. 如图,在等腰△ABC中,点M,N都在BC边上,∠BAC=120°,若ME⊥AB于点E,NF⊥AC于点F,点E,F分别为AB,AC的中点,且EM=2.则BC的长为( ) A、6 B、8 C、10 D、12
A、6 B、8 C、10 D、12二、填空题
-
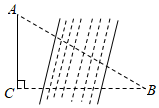
11. 如图,某研究性学习小组为测量学校A与河对岸水上乐园B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=1km.据此,可求得学校与水上乐园之间的距离AB等于 km.
 12. 如图,在Rt△ABC中,∠ACB=90°,D为AB上异于A,B的一点,AC≠BC.
12. 如图,在Rt△ABC中,∠ACB=90°,D为AB上异于A,B的一点,AC≠BC. (1)、若D为AB中点,且 CD=2,则AB=.(2)、当CD= AB时,∠A=α ,要使点D必为AB的中点,则α的取值范围是.13. 如图,在△ABC中,∠ACB=90°,∠A=30°,边AC的垂直平分线DE分别交边AB、AC于点D、E、P为直线DE上一点.若BC=2,则△BCP周长的最小值为 .
(1)、若D为AB中点,且 CD=2,则AB=.(2)、当CD= AB时,∠A=α ,要使点D必为AB的中点,则α的取值范围是.13. 如图,在△ABC中,∠ACB=90°,∠A=30°,边AC的垂直平分线DE分别交边AB、AC于点D、E、P为直线DE上一点.若BC=2,则△BCP周长的最小值为 .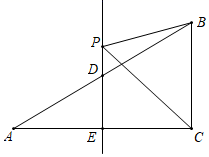 14. 如图,在△ABC中,∠ACB=90°,∠B =30°,CD是高.若AD=2,则BD= .
14. 如图,在△ABC中,∠ACB=90°,∠B =30°,CD是高.若AD=2,则BD= . 15. 如图,∠AOE=∠BOE=15°,EF//OB,EC⊥OB,若EC=2,则EF= .
15. 如图,∠AOE=∠BOE=15°,EF//OB,EC⊥OB,若EC=2,则EF= . 16. 如图,在中, , , , EF是AC的垂直平分线,P是直线EF上的任意一点,则的最小值是 .
16. 如图,在中, , , , EF是AC的垂直平分线,P是直线EF上的任意一点,则的最小值是 . 17. 如图,在中, , , 交BC于点D.若 , 则 .
17. 如图,在中, , , 交BC于点D.若 , 则 . 18. 一个直角三角形房梁如图所示,其中 , , AB=10m, , 垂足为D,那么BD .
18. 一个直角三角形房梁如图所示,其中 , , AB=10m, , 垂足为D,那么BD . 19. 如上图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=6,则PD=
19. 如上图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=6,则PD= 20. 如图,线段AB=4,E为AB中点,点C、D为直线AB同侧不重合的两点,且∠ACB=∠ADB=90°,连接CE、DE、CD,设△CDE的面积为S,则S的范围是.
20. 如图,线段AB=4,E为AB中点,点C、D为直线AB同侧不重合的两点,且∠ACB=∠ADB=90°,连接CE、DE、CD,设△CDE的面积为S,则S的范围是.
三、解答题
-
21. 如图,在中,∠°,∠°,⊥AB于点D,交AC于点E,如果 , 求的长.
 22. 如图,△ABC中,∠C=90°.
22. 如图,△ABC中,∠C=90°.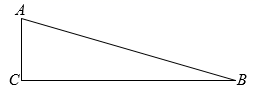 (1)、求作△AEB , 使△AEB是以AB为底的等腰三角形,且使点E在边BC上.(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)所作的图形中,若∠CAE:∠EAB=4:1,求∠AEB的度数;(3)、在(2)的条件下,求证:BE=2AC .23. 如图,在中, , , 是边上的点,且 , 过点作边的垂线交边于点 , 求的长.
(1)、求作△AEB , 使△AEB是以AB为底的等腰三角形,且使点E在边BC上.(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)所作的图形中,若∠CAE:∠EAB=4:1,求∠AEB的度数;(3)、在(2)的条件下,求证:BE=2AC .23. 如图,在中, , , 是边上的点,且 , 过点作边的垂线交边于点 , 求的长.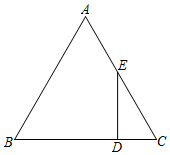 24. 如图,在 中, 于点D , 若 ,求 的长.
24. 如图,在 中, 于点D , 若 ,求 的长. 25. 如图,AF,AD分别是 的高和角平分线,且 , ,求 的度数.
25. 如图,AF,AD分别是 的高和角平分线,且 , ,求 的度数.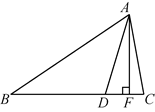
四、综合题
-
26. 如图, 和 中, , 与 交于点P(不与点B,C重合),点B,E在 异侧, 、 的平分线相交于点I.
 (1)、当 时,求 的长;(2)、求证: ;(3)、当 时, 的取值范围为 ,求m,n的值.27. 问题情境:
(1)、当 时,求 的长;(2)、求证: ;(3)、当 时, 的取值范围为 ,求m,n的值.27. 问题情境:七下教材第149页提出这样一个问题:如图1,∠AOB=90°,OC平分∠AOB,把三角尺的直角顶点落在OC的任意一点P上,并使三角尺的两条直角边分别与OA、OB相交于点E、F,PE与PF相等吗?
 (1)、七年级学习这部分内容时,我们还无法对这个问题的结论加以证明,八下教材第59页第11题不仅对这一问题给出了答案:“通过实验可以得到PE=PF”,还要求“现在请你证明这个结论”,请你给出证明:(2)、变式拓展:
(1)、七年级学习这部分内容时,我们还无法对这个问题的结论加以证明,八下教材第59页第11题不仅对这一问题给出了答案:“通过实验可以得到PE=PF”,还要求“现在请你证明这个结论”,请你给出证明:(2)、变式拓展:
如图2,已知∠AOB=120°,OC平分∠AOB,P是OC上一点,∠EPF=60°,PE边与OA边相交于点E,PF边与射线OB的反向延长线相交于点F.试解决下列问题:①PE与PF还相等吗?为什么?
②试判断OE、OF、OP三条线段之间的数量关系,并说明理由.
28. 如图: ,点P是 角平分线上一点,过点P作PC平行OA交OB于点C, 于点D,若 .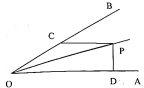 (1)、求证: 是等腰三角形.(2)、求 的长.
(1)、求证: 是等腰三角形.(2)、求 的长.