2022-2023学年浙教版数学八年级上册2.5 逆命题和逆定理 同步练习
试卷更新日期：2022-07-04 类型：同步测试
一、单选题
-
1. 下列命题中，其逆命题是真命题的命题个数有（ ）
⑴全等三角形的对应边相等； ⑵对顶角相等；
⑶等角对等边； ⑷全等三角形的面积相等．
A、1个 B、2个 C、3个 D、4个2. 下列命题中，逆命题错误的是（ ）A、两直线平行，同旁内角互补 B、对顶角相等 C、直角三角形的两个锐角互余 D、直角三角形两条直角边的平方和等于斜边的平方3. “对顶角相等”的逆命题是（ ）A、如果两个角是对顶角，那么这两个角相等 B、如果两个角相等，那么这两个角是对顶角 C、如果两个角不是对顶角，那么这两个角不相等 D、如果两个角不相等，那么这两个角不是对顶角4. 下列定理中没有逆定理的是（ ）A、两直线平行，内错角相等 B、角平分线上的点到这个角两边的距离相等 C、对顶角相等 D、在同一个三角形中，等边对等角5. 下列命题：①成轴对称的两个三角形是全等三角形；②当a＞b时，若c＞0，则ac＞bc；③直角三角形中斜边上的中线等于斜边的一半；④内错角相等，其中原命题与逆命题均为真命题的个数是（ ）A、1个 B、2个 C、3个 D、4个6. 以下命题的逆命题为真命题的是（ ）A、邻补角相等 B、同旁内角互补，两直线平行 C、若 ，则 D、若 ，则7. 对于下列命题：①若a2＞b2 ， 则|a|＞|b|；②若a+b＝0，则|a|＝|b|；③等边三角形的三个内角都相等；其中原命题与逆命题均为真命题的是（ ）A、①②③ B、①② C、①③ D、②③8. 下列命题中，逆命题是真命题的是（ ）A、对顶角相等 B、全等三角形的对应角相等 C、若 ，则 ． D、若 ，则9. 下列命题的逆命题是假命题的是（ ）A、直角三角形的两个锐角互余 B、有两边相等的三角形是等腰三角形 C、相等的两个角是对顶角 D、如果a＞0，b＞0，那么a+b＞010. 下列命题的逆命题一定成立的是（ ）A、在三角形中，等边对等角 B、全等三角形的对应角相等 C、若 ，则 D、若 ，则二、填空题
-
11. “等腰三角形底边上的高线与中线互相重合”的逆命题是 ． 这个逆命题是命题．（真、假）12. “全等三角形的对应边相等”的逆命题是： ．13. 写出命题“直角三角形的两个锐角互余”的逆命题： ．14. 命题“如果ab＝0，那么a+b＝0”的逆命题为 ．15. 已知命题：“如果两个三角形全等，那么这两个三角形的面积相等.”写出它的逆命题： ， 该逆命题是命题（填“真”或“假”）.16. 把命题：“内错角相等”改写成“如果…那么…”的形式是；该命题是命题（填“真”或“假”）.17. 命题“若a2＞b2则a＞b”是命题（填“真”或“假”），它的逆命题是 ．18. 写出命题“全等三角形的周长相等”的逆命题： ．19. “对顶角相等”这个命题的逆命题是.20. 请写出定理：“等腰三角形的两个底角相等”的逆定理 ．
三、解答题
-
21. 写出命题：“等腰三角形两腰上的高相等”的逆命题，并证明其逆命题是真命题.（要求写出已知、求证和证明过程）
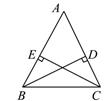.22. 已知命题：“P 是等边△ABC 内的一点，若 P 到三边的距离相等，则 PA=PB=PC．”
(1)、写出它的逆命题．判断其逆命题成立吗？若成立，请给出证明．(2)、进一步证明：点 P 到等边△ABC 各边的距离之和为定值．
23. 按要求完成下列各小题．（1）请写出以下命题的逆命题：
①相等的角是内错角；
②如果a+b＞0，那么ab＞0；
（2）判断（1）中①的原命题和逆命题是否为逆定理．
24. 写出以下命题的逆命题，判断逆命题的真假．若为假命题，请举反例；若为真命题，请给予证明．（1）一次函数y=kx+b，若k＞0，b＜0，则它的图象不经过第二象限；
（2）等腰三角形底边上的中点到两腰的距离相等．
25. 写出下列命题的逆命题，并判断逆命题是真命题，还是假命题．(1)、两直线平行，同位角相等(2)、如果两个数相等，那么这两个数的绝对值相等．26.(1)、写出命题“等腰三角形底边上的高线与中线互相重合”的逆命题，并判断真假；(2)、若该命题的逆命题为真命题，请证明；若该命题的逆命题为假命题，请举出反例.27. 写出下列命题的逆命题：(1)、两条直线被第三条直线所截，如果有一对同位角相等，那么这两条直线平行；(2)、角平分线上的点到角的两边的距离相等；(3)、若r²=a，则r叫a的平方根；(4)、如果a≥0，那么 =a．