2022-2023学年浙教版数学八年级上册2.4 等腰三角形的判定定理 同步练习
试卷更新日期:2022-07-04 类型:同步测试
一、单选题
-
1. 如图,等边 中,D为AC中点,点P、Q分别为AB、AD上的点, , ,在BD上有一动点E,则 的最小值为( )
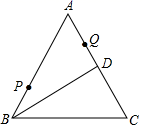 A、7 B、8 C、10 D、122. 下列命题是真命题的是( )A、两直线平行,同旁内角相等 B、有一个角是60°的三角形是等边三角形 C、有两条边和一个角对应相等的两个三角形一定全等 D、到一条线段的两端距离相等的点,必在这条线段的垂直平分线上3. 如图, 中, , , ,垂足为Q,延长MN至G,取 ,若 的周长为12, ,则 周长是( )
A、7 B、8 C、10 D、122. 下列命题是真命题的是( )A、两直线平行,同旁内角相等 B、有一个角是60°的三角形是等边三角形 C、有两条边和一个角对应相等的两个三角形一定全等 D、到一条线段的两端距离相等的点,必在这条线段的垂直平分线上3. 如图, 中, , , ,垂足为Q,延长MN至G,取 ,若 的周长为12, ,则 周长是( )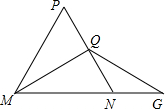 A、8+2m B、8+m C、6+2m D、6+m4. 如图,在中,运用尺规作图的方法在BC边上取一点P,使 , 下列作法正确的是( )A、
A、8+2m B、8+m C、6+2m D、6+m4. 如图,在中,运用尺规作图的方法在BC边上取一点P,使 , 下列作法正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,△ABC中,直线l是边AB的垂直平分线,若直线l上存在点P,使得△PAC,△PAB均为等腰三角形,则满足条件的点P的个数共有( )
5. 如图,△ABC中,直线l是边AB的垂直平分线,若直线l上存在点P,使得△PAC,△PAB均为等腰三角形,则满足条件的点P的个数共有( ) A、1 B、3 C、5 D、76. 如图所示,点E、F为网格中的格点,为等腰三角形,且点D是网格中的格点,则符合条件的三角形点D有( )
A、1 B、3 C、5 D、76. 如图所示,点E、F为网格中的格点,为等腰三角形,且点D是网格中的格点,则符合条件的三角形点D有( )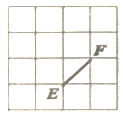 A、4个 B、6个 C、9个 D、10个7. 如图,已知Rt△ABC中,∠C=90°,∠A=30°,在直线BC上取一点P,使得△PAB是等腰三角形,则符合条件的点P有( )
A、4个 B、6个 C、9个 D、10个7. 如图,已知Rt△ABC中,∠C=90°,∠A=30°,在直线BC上取一点P,使得△PAB是等腰三角形,则符合条件的点P有( ) A、1个 B、2个 C、3个 D、4个8. 如图,是等边中边上的点, , , 则是( )
A、1个 B、2个 C、3个 D、4个8. 如图,是等边中边上的点, , , 则是( )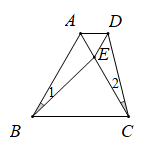 A、等腰三角形 B、等边三角形 C、不等边三角形 D、无法确定9. 如图, 中, , ,BD平分 交AC于点D,则图中的等腰三角形共有( )个.
A、等腰三角形 B、等边三角形 C、不等边三角形 D、无法确定9. 如图, 中, , ,BD平分 交AC于点D,则图中的等腰三角形共有( )个. A、2 B、3 C、4 D、510. 如图,在 中, , , , , ,则 ( )
A、2 B、3 C、4 D、510. 如图,在 中, , , , , ,则 ( )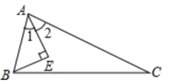 A、10 B、11 C、13 D、15
A、10 B、11 C、13 D、15二、填空题
-
11. 如图, 、 的平分线相交于点F,过F作 ,交 于点D,交 于点E, , ,则 .
 12. 如图, 平分 交 于点E,若 ,则 .
12. 如图, 平分 交 于点E,若 ,则 . 13. 如图,在等边三角形ABC中, 的平分线与 的平分线相交于D,过点D作 交AB于E,交AC于F, ,则BC的长为.
13. 如图,在等边三角形ABC中, 的平分线与 的平分线相交于D,过点D作 交AB于E,交AC于F, ,则BC的长为. 14. 在平面直角坐标系xOy中,横、纵坐标都是整数的点叫做整点.如图,点的坐标为( , 4),点的坐标为( , 1),点为第一象限内的整点,不共线的 , , 三点构成轴对称图形,则点的坐标可以是(写出一个即可),满足题意的点的个数为 .
14. 在平面直角坐标系xOy中,横、纵坐标都是整数的点叫做整点.如图,点的坐标为( , 4),点的坐标为( , 1),点为第一象限内的整点,不共线的 , , 三点构成轴对称图形,则点的坐标可以是(写出一个即可),满足题意的点的个数为 . 15. 如图,在中, , , 点在线段上运动(不与 , 重合),连接 , 作 , 与交于.在点的运动过程中,的度数为时,的形状是等腰三角形.
15. 如图,在中, , , 点在线段上运动(不与 , 重合),连接 , 作 , 与交于.在点的运动过程中,的度数为时,的形状是等腰三角形. 16. 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,AD=4,CD=2,那么∠A=度.
16. 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,AD=4,CD=2,那么∠A=度.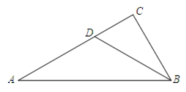 17. 在中, , . 用无刻度的直尺和圆规在边上找一点D,使为等腰三角形.下列作法正确的有个.
17. 在中, , . 用无刻度的直尺和圆规在边上找一点D,使为等腰三角形.下列作法正确的有个. 18. 如图,在中,BD和CD分别是和的平分线,EF过点D,且 , 若 , , 则EF的长为 .
18. 如图,在中,BD和CD分别是和的平分线,EF过点D,且 , 若 , , 则EF的长为 . 19. 如图所示,已知∠AOB=40°,现按照以下步骤作图:①在OA,OB上分别截取线段OD,OE,使OD=OE;②分别以D,E为圆心,以DE长为半径画弧,在∠AOB内两弧交于点C;③作射线OC;④连接DC、EC.则∠OEC的度数为 .
19. 如图所示,已知∠AOB=40°,现按照以下步骤作图:①在OA,OB上分别截取线段OD,OE,使OD=OE;②分别以D,E为圆心,以DE长为半径画弧,在∠AOB内两弧交于点C;③作射线OC;④连接DC、EC.则∠OEC的度数为 . 20. 如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论中正确的有(填序号)①△BPQ是等边三角形②△PCQ是直角三角形③∠APB=150° ④∠APC=120°
20. 如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论中正确的有(填序号)①△BPQ是等边三角形②△PCQ是直角三角形③∠APB=150° ④∠APC=120°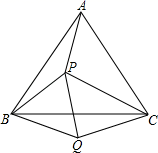
三、解答题
-
21. 如图,在△ABC中,AB=AC,高BD、CE相于点O.证明OB=OC.
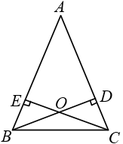 22. “三等分角”是被称为几何三大难题的三个古希腊作图难题之一.如图1所示的“三等分角仪”是利用阿基米德原理做出的.这个仪器由两根有槽的棒PA,PB组成,两根棒在P点相连并可绕点P旋转,C点是棒PA上的一个固定点,点A,O可在棒PA,PB内的槽中滑动,且始终保持OA=OC=PC.∠AOB为要三等分的任意角.则利用“三等分角仪”可以得到∠APB =∠AOB.
22. “三等分角”是被称为几何三大难题的三个古希腊作图难题之一.如图1所示的“三等分角仪”是利用阿基米德原理做出的.这个仪器由两根有槽的棒PA,PB组成,两根棒在P点相连并可绕点P旋转,C点是棒PA上的一个固定点,点A,O可在棒PA,PB内的槽中滑动,且始终保持OA=OC=PC.∠AOB为要三等分的任意角.则利用“三等分角仪”可以得到∠APB =∠AOB.我们把“三等分角仪”抽象成如图2所示的图形,完成下面的证明.
已知:如图2,点O,C分别在∠APB的边PB,PA上,且OA=OC=PC.
求证:∠APB =∠AOB.
 23. 如图,在△ABC中,AB=AC,D为AB边的中点,DE⊥AC于点E,DF⊥BC于点F,DE=DF.求证:△ABC是等边三角形.
23. 如图,在△ABC中,AB=AC,D为AB边的中点,DE⊥AC于点E,DF⊥BC于点F,DE=DF.求证:△ABC是等边三角形.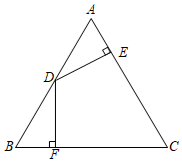 24. 如图,在△ABC中,AB=AC,分别以为圆心,BC长为半径作弧,两弧交于点D,连接BD、CD.求∠CDA的度数.
24. 如图,在△ABC中,AB=AC,分别以为圆心,BC长为半径作弧,两弧交于点D,连接BD、CD.求∠CDA的度数.
四、综合题
-
25. 如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE于B,DE⊥BE于E,且AB=DE,BF=CE.求证:
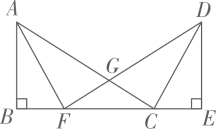 (1)、GF=GC;(2)、△AFG≌△DCG.26. 如图:点E、F在BC上, , , ,AF与DE交于点G.过点G作 ,垂足为H.
(1)、GF=GC;(2)、△AFG≌△DCG.26. 如图:点E、F在BC上, , , ,AF与DE交于点G.过点G作 ,垂足为H.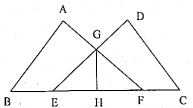 (1)、求证:(2)、求证:
(1)、求证:(2)、求证:


