2022-2023学年浙教版数学八年级上册2.1 图形的轴对称 同步练习
试卷更新日期:2022-07-04 类型:同步测试
一、单选题
-
1. 下面4个图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中,不一定是轴对称图形的是( )A、直角三角形 B、等腰三角形 C、等边三角形 D、正方形3. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
2. 下列图形中,不一定是轴对称图形的是( )A、直角三角形 B、等腰三角形 C、等边三角形 D、正方形3. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 篆体是我国古代汉字书体之一,下列篆体字“复”,“兴”,“之”,“路”中,是轴对称图形的是( )A、
4. 篆体是我国古代汉字书体之一,下列篆体字“复”,“兴”,“之”,“路”中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列图案中,属于轴对称图形的是( )A、
5. 下列图案中,属于轴对称图形的是( )A、 B、
B、 C、
C、 D、
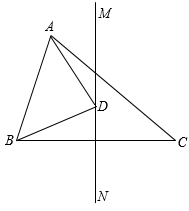
D、 6. 如图,点P在锐角 的内部,连接 , ,点P关于 、 所在直线的对称点分别是 、 ,则 、 两点之间的距离可能是( )
6. 如图,点P在锐角 的内部,连接 , ,点P关于 、 所在直线的对称点分别是 、 ,则 、 两点之间的距离可能是( ) A、8 B、7 C、6 D、57. 如图,直线MN是四边形MANB的对称轴,点P在MN上.则下列结论错误的是( )
A、8 B、7 C、6 D、57. 如图,直线MN是四边形MANB的对称轴,点P在MN上.则下列结论错误的是( )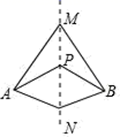 A、AM=BM B、AP=BN C、∠ANM=∠BNM D、∠MAP=∠MBP8. 如图4所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,
A、AM=BM B、AP=BN C、∠ANM=∠BNM D、∠MAP=∠MBP8. 如图4所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,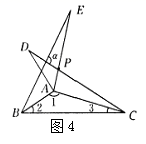
若∠1:∠2:∠3=28:5:3,则∠α的度数是( )
A、80° B、100° C、60° D、45°.9. 如图,直线 , 表示一条河的两岸,且 ∥ 现要在这条河上建一座桥(桥与河的两岸相互垂直),使得从村庄A经桥过河到村庄B的路程最短,应该选择路线( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在2×4 的网格图中, ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在该网格图中与 ABC成轴对称的格点三角形一共有( )
10. 如图,在2×4 的网格图中, ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在该网格图中与 ABC成轴对称的格点三角形一共有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,在中, , . 为边上的垂直平分线,若点D在直线上,连接 , , 则周长的最小值为 .
 12. 如图,在四边形ABCD中,∠BCD=50°,∠B=∠D=90°,在BC、CD上分别取一点M、N,使△AMN的周长最小,则∠MAN=°.
12. 如图,在四边形ABCD中,∠BCD=50°,∠B=∠D=90°,在BC、CD上分别取一点M、N,使△AMN的周长最小,则∠MAN=°.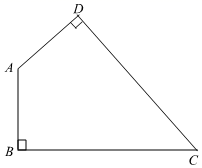 13. 如图,在△ABC中,AB=AC,BC=5,△ABC的面积为20,DE垂直平分AC,分别交边AB,AC于点D,E,点F为直线DE上一动点,点G为BC的中点,连接FG,FC,则FC+FG的最小值为 .
13. 如图,在△ABC中,AB=AC,BC=5,△ABC的面积为20,DE垂直平分AC,分别交边AB,AC于点D,E,点F为直线DE上一动点,点G为BC的中点,连接FG,FC,则FC+FG的最小值为 . 14. 如图,的顶点都在正方形网格的格点上,点A的坐标为 , 将沿坐标轴翻折,则点C的对应点的坐标是 .
14. 如图,的顶点都在正方形网格的格点上,点A的坐标为 , 将沿坐标轴翻折,则点C的对应点的坐标是 .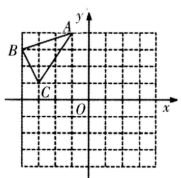 15. 如图,BD是△ABC的角平分线,E和F分别是AB和AD上的动点,已知△ABC的面积是12cm2 , BC的长是8cm,则AF+EF的最小值是cm.
15. 如图,BD是△ABC的角平分线,E和F分别是AB和AD上的动点,已知△ABC的面积是12cm2 , BC的长是8cm,则AF+EF的最小值是cm.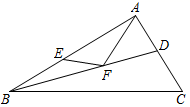 16. 如图,等腰三角形ABC的底边BC长为3,面积是18,腰AC的垂直平分线分别交AC、AB边于点E、F.若点D为DC边的中点,点M为线段EF上一动点,则CDM周长的最小值为 .
16. 如图,等腰三角形ABC的底边BC长为3,面积是18,腰AC的垂直平分线分别交AC、AB边于点E、F.若点D为DC边的中点,点M为线段EF上一动点,则CDM周长的最小值为 .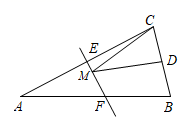 17. 如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交边BC于点D,E,F分别是AD,AC上的点,连接CE,EF.若AB=10,BC=6,AC=8,则CE+EF的最小值是.
17. 如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交边BC于点D,E,F分别是AD,AC上的点,连接CE,EF.若AB=10,BC=6,AC=8,则CE+EF的最小值是. 18. 图中与标号“1”的三角形成轴对称的三角形的个数为 .
18. 图中与标号“1”的三角形成轴对称的三角形的个数为 .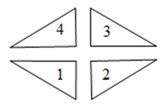
三、解答题
-
19. 在下图给出一个图案的左半部分,其中虚线是这个图案的对称轴.请你画出这个图案的右半部分,使它组成一个完整的图案.
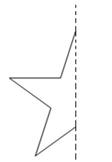 20. 在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,点B的坐标为 .
20. 在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,点B的坐标为 .
( 1 )作出 关于x轴对称的 ,并写出点 的坐标;
( 2 )作出 关于y轴对称的 ,并写出点 的坐标,
21. 如图,利用关于坐标轴对称的点的坐标的特点,作出 ABC关于x轴对称的图形. 22. 如图所示,在平面直角坐标系中△ABC的三个顶点坐标分别为A(﹣2,4),B(-4,2),C(﹣3,1).
22. 如图所示,在平面直角坐标系中△ABC的三个顶点坐标分别为A(﹣2,4),B(-4,2),C(﹣3,1).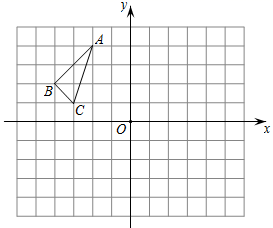
(1)作出△ABC关于x轴对称的△A1B1C1 , 并直接写出A1点的坐标
(2)作出△ABC关于y轴对称的△A2B2C2 , 并直接写出B2点的坐标
(3)在(1)(2)的条件下,若点P在x轴上,当A1P+B2P的值最小时,直接写出A1P+B2P的最小值23. 如图, 三个顶点的坐标分别为 , , .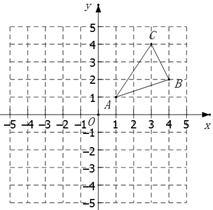
(1)请画出 关于x轴成轴对称的图形 ,并写出 、 、 的坐标;
(2)求 的面积;(3)在y轴上找一点P,使 的值最小,请画出点P的位置.
四、综合题
-
24. 在下面的方格纸中作图:
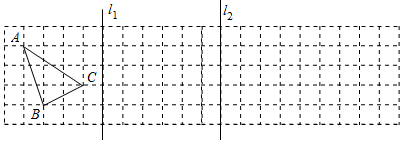 (1)、先画△ABC关于直线l1的对称图形△A1B1C1 , 再画△A1B1C1关于直线l2的对称图形△A2B2C2;(2)、若△ABC向右平移1格,则△A2B2C2向平移格.25. 如图,方格纸中的每个小方格都是边长为1个单位的小正方形,每个小正方形的顶点称为格点,△ABC的顶点都在格点上,建立平面直角坐标系后,点A,B,C的坐标分别为(1,1),(4,2),(2,3).
(1)、先画△ABC关于直线l1的对称图形△A1B1C1 , 再画△A1B1C1关于直线l2的对称图形△A2B2C2;(2)、若△ABC向右平移1格,则△A2B2C2向平移格.25. 如图,方格纸中的每个小方格都是边长为1个单位的小正方形,每个小正方形的顶点称为格点,△ABC的顶点都在格点上,建立平面直角坐标系后,点A,B,C的坐标分别为(1,1),(4,2),(2,3). (1)、画出△ABC向左平移4个单位,再向上平移1个单位后得到的△A1B1C1;(2)、画出△ABC向关于x轴对称的△A2B2C2;(3)、以点A、A1、A2为顶点的三角形的面积为.26. 如图,P为内一定点,M、N分别是射线OA、OB上的点,
(1)、画出△ABC向左平移4个单位,再向上平移1个单位后得到的△A1B1C1;(2)、画出△ABC向关于x轴对称的△A2B2C2;(3)、以点A、A1、A2为顶点的三角形的面积为.26. 如图,P为内一定点,M、N分别是射线OA、OB上的点, (1)、当周长最小时,在图中画出(保留作图痕迹);(2)、在(1)的条件下,已知 , 求的度数.27. 如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
(1)、当周长最小时,在图中画出(保留作图痕迹);(2)、在(1)的条件下,已知 , 求的度数.27. 如图,在平面直角坐标系中,直线l是第一、三象限的角平分线. (1)、实验与探究:
(1)、实验与探究:观察图,易知A(0,2)关于直线l的对称点的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点、的位置,并写出他们的坐标: , ;
(2)、归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点的坐标为(不必证明);(3)、运用与拓广:已知两点D(1,﹣3)、E(﹣3,﹣4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小.28. 如图,在平面直角坐标系中,三个顶点的坐标为、、 . (1)、在图中作出关于轴的对称图形;(2)、请直接写出点的坐标;(3)、在轴上画出一点使的值最小.
(1)、在图中作出关于轴的对称图形;(2)、请直接写出点的坐标;(3)、在轴上画出一点使的值最小.