2022-2023学年浙教版数学八年级上册1.5 三角形全等的判定 同步练习
试卷更新日期:2022-07-04 类型:同步测试
一、单选题
-
1. 王师傅用4根木条钉成一个四边形木架,如图,要使这个木架不变形,他至少还要再钉上几根木条?( )
 A、0根 B、1根 C、2根 D、3根2. 如图, , ,欲证 ,则可增加的条件是( )
A、0根 B、1根 C、2根 D、3根2. 如图, , ,欲证 ,则可增加的条件是( ) A、 B、 C、 D、3. 如图, 中, 的垂直平分线 交 的平分线 于点 ,过 作 于点 ,若 , ,则 ( )
A、 B、 C、 D、3. 如图, 中, 的垂直平分线 交 的平分线 于点 ,过 作 于点 ,若 , ,则 ( )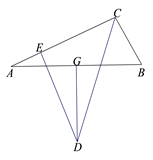 A、 B、 C、 D、4. 如图,在 的网格中,每一个小正方形的边长都是1,点 , , , 都在格点上,连接 , 相交于 ,那么 的大小是( )
A、 B、 C、 D、4. 如图,在 的网格中,每一个小正方形的边长都是1,点 , , , 都在格点上,连接 , 相交于 ,那么 的大小是( )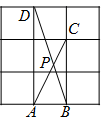 A、 B、 C、 D、5. 如图, 平分 ,点P在 上,且 ,垂足为D,若 ,则P到 的距离d满足( )
A、 B、 C、 D、5. 如图, 平分 ,点P在 上,且 ,垂足为D,若 ,则P到 的距离d满足( ) A、 B、 C、 D、无法确定6. 如图,三条笔直的公路两两相交,交点分别在点A、B、C处,有两户村民分别在点D和点E处,现准备建造一个蓄水池,要求水池到两条公路AB、BC的距离相等,且到两户村民D、E的距离相等,则水池修建的位置应该是( )
A、 B、 C、 D、无法确定6. 如图,三条笔直的公路两两相交,交点分别在点A、B、C处,有两户村民分别在点D和点E处,现准备建造一个蓄水池,要求水池到两条公路AB、BC的距离相等,且到两户村民D、E的距离相等,则水池修建的位置应该是( ) A、在∠B的平分线与DE的交点处 B、在线段AB、AC的垂直平分线的交点处 C、在∠B的平分线与DE的垂直平分线的交点处 D、在∠A的平分线与DE的垂直平分线的交点处7. 尺规作图:作 角等于已知角 .示意图如图所示,则说明 的依据是( )
A、在∠B的平分线与DE的交点处 B、在线段AB、AC的垂直平分线的交点处 C、在∠B的平分线与DE的垂直平分线的交点处 D、在∠A的平分线与DE的垂直平分线的交点处7. 尺规作图:作 角等于已知角 .示意图如图所示,则说明 的依据是( )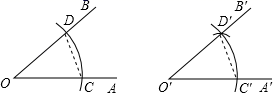 A、SSS B、SAS C、ASA D、AAS8. 如图,已知AB=AD,AC=AE,若要判定△ABC≌△ADE,则下列添加的条件中正确的是( )
A、SSS B、SAS C、ASA D、AAS8. 如图,已知AB=AD,AC=AE,若要判定△ABC≌△ADE,则下列添加的条件中正确的是( ) A、∠1=∠DAC B、∠B=∠D C、∠1=∠2 D、∠C=∠E9. 如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形.他的依据是( )
A、∠1=∠DAC B、∠B=∠D C、∠1=∠2 D、∠C=∠E9. 如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形.他的依据是( ) A、 B、 C、 D、10. 如图,点B,C,E在同一直线上,且 , , ,下列结论不一定成立的是( )
A、 B、 C、 D、10. 如图,点B,C,E在同一直线上,且 , , ,下列结论不一定成立的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图, 与 中,已知, ,请你添加一个条件(不添加字母和辅助线),使 ,你添加的条件是.
 12. 如图,在 中, , 平分 , ,点D到 的距离为5.6,则 .
12. 如图,在 中, , 平分 , ,点D到 的距离为5.6,则 . 13. 如图,已知CB⊥AD , AE⊥CD , 垂足分别为B , E , AE、BC相交于点F , 若AB=BC=8,CF=2,连结DF , 则图中阴影部分面积为 .
13. 如图,已知CB⊥AD , AE⊥CD , 垂足分别为B , E , AE、BC相交于点F , 若AB=BC=8,CF=2,连结DF , 则图中阴影部分面积为 . 14. 如图,已知 中, 平分 ,且 ,则点D到 边的距离为.
14. 如图,已知 中, 平分 ,且 ,则点D到 边的距离为. 15. 如图,已知 的周长是22,PB、PC分别平分 和 , 于D,且 , 的面积是.
15. 如图,已知 的周长是22,PB、PC分别平分 和 , 于D,且 , 的面积是.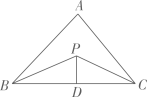 16. 如图,在 △ABC 中,BE平分 ∠ABC , AE⊥BE 于点E, △BCE 的面积为2,则 △ABC 的面积是.
16. 如图,在 △ABC 中,BE平分 ∠ABC , AE⊥BE 于点E, △BCE 的面积为2,则 △ABC 的面积是. 17. 如图,DE=AC,∠1=∠2,要使△DBE≌△ABC还需添加一个条件是 .(只需写出一种情况)
17. 如图,DE=AC,∠1=∠2,要使△DBE≌△ABC还需添加一个条件是 .(只需写出一种情况) 18. 如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=5,若△BCE的面积为5,则ED的长为 .
18. 如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=5,若△BCE的面积为5,则ED的长为 .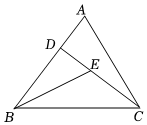 19. 在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=2cm,过点E作EF⊥AC交CD的延长线于点F.若AE=3cm,则EF=cm.
19. 在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=2cm,过点E作EF⊥AC交CD的延长线于点F.若AE=3cm,则EF=cm. 20. 如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N分别是BD、BC上的动点,则CM+MN的最小值为
20. 如图,在锐角三角形ABC中,AB=4,△ABC的面积为10,BD平分∠ABC,若M、N分别是BD、BC上的动点,则CM+MN的最小值为
三、解答题
-
21. 如图, 是 的中线,F为 上一点,E为 延长线上一点,且 .求证: .
 22. 如图,已知点E、C在线段BF上, , , .求证:
22. 如图,已知点E、C在线段BF上, , , .求证: .
.  23. 如图,已知△ACD的周长是14,AB-AC=2,BC的垂直平分线交AB于点D,交BC于点E,求AB和AC的长.
23. 如图,已知△ACD的周长是14,AB-AC=2,BC的垂直平分线交AB于点D,交BC于点E,求AB和AC的长. 24. 如图, 、 相交于点O, , .E、F分别为 、 的中点.求证 .
24. 如图, 、 相交于点O, , .E、F分别为 、 的中点.求证 . 25. 已知:如图,点B,F在线段EC上, , , .求证: .
25. 已知:如图,点B,F在线段EC上, , , .求证: .
四、综合题
-
26. 如图,点D在AC上,BC,DE交于点F, , , .
 (1)、求证: ;(2)、若 ,求∠CDE的度数.27. 在 中, , ,直线 经过点 ,且 于 , 于 .(1)、当直线 绕点 旋转到图1的位置时,
(1)、求证: ;(2)、若 ,求∠CDE的度数.27. 在 中, , ,直线 经过点 ,且 于 , 于 .(1)、当直线 绕点 旋转到图1的位置时,
①求证: ≌ ;
②求证: ;
(2)、当直线 绕点 旋转到图2的位置时,(1)中的结论②还成立吗?若成立,请给出证明;若不成立,说明理由. 28. 如图,点D在 的BC边上, , , .
28. 如图,点D在 的BC边上, , , . (1)、求证: ;(2)、若 , ,求CD的长,29. 小明与爸爸妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1.2m高的B处接住他后用力一推,爸爸在C处接住他,若妈妈与爸爸到OA的水平距离BD、CE分别为1.6m和2m,∠BOC=90°.
(1)、求证: ;(2)、若 , ,求CD的长,29. 小明与爸爸妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1.2m高的B处接住他后用力一推,爸爸在C处接住他,若妈妈与爸爸到OA的水平距离BD、CE分别为1.6m和2m,∠BOC=90°.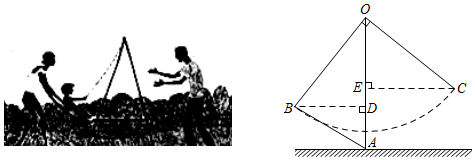 (1)、△OBD与△COE全等吗?请说明理由;(2)、爸爸是在距离地面多高的地方接住小明的?30. 直线l经过点A, 在直线l上方, .
(1)、△OBD与△COE全等吗?请说明理由;(2)、爸爸是在距离地面多高的地方接住小明的?30. 直线l经过点A, 在直线l上方, . (1)、如图1, ,过点B,C作直线l的垂线,垂足分别为D、E.求证:(2)、如图2,D,A,E三点在直线l上,若 ( 为任意锐角或钝角),猜想线段DE、BD、CE有何数量关系?并给出证明.(3)、如图3, 过点B作直线l上的垂线,垂足为F,点D是BF延长线上的一个动点,连结AD,作 ,使得 ,连结DE,CE.直线l与CE交于点G.求证:G是CE的中点.
(1)、如图1, ,过点B,C作直线l的垂线,垂足分别为D、E.求证:(2)、如图2,D,A,E三点在直线l上,若 ( 为任意锐角或钝角),猜想线段DE、BD、CE有何数量关系?并给出证明.(3)、如图3, 过点B作直线l上的垂线,垂足为F,点D是BF延长线上的一个动点,连结AD,作 ,使得 ,连结DE,CE.直线l与CE交于点G.求证:G是CE的中点.