2022-2023学年浙教版数学八年级上册1.4 全等三角形 同步练习
试卷更新日期:2022-07-04 类型:同步测试
一、单选题
-
1. 下列图形是全等图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中被虚线分成的两部分不是全等图形的是( )A、
2. 下列图形中被虚线分成的两部分不是全等图形的是( )A、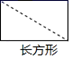 B、
B、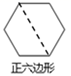 C、
C、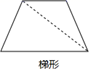 D、
D、 3. 下列说法正确的是( )A、两个面积相等的图形一定是全等形 B、两个等边三角形是全等形 C、若两个图形的周长相等,则它们一定是全等形 D、两个全等图形的面积一定相等4. △ABC≌△DEF,且△ABC的周长为100cm,A、B分别与D、E对应,且AB=35cm,DF=30cm,则EF的长为( )A、35cm B、30cm C、45cm D、55cm5. 如图,△ABC≌△DEF,点B、E、C、F在同一直线上,若BC=7,EC=4,则CF的长是( )
3. 下列说法正确的是( )A、两个面积相等的图形一定是全等形 B、两个等边三角形是全等形 C、若两个图形的周长相等,则它们一定是全等形 D、两个全等图形的面积一定相等4. △ABC≌△DEF,且△ABC的周长为100cm,A、B分别与D、E对应,且AB=35cm,DF=30cm,则EF的长为( )A、35cm B、30cm C、45cm D、55cm5. 如图,△ABC≌△DEF,点B、E、C、F在同一直线上,若BC=7,EC=4,则CF的长是( ) A、2 B、3 C、4 D、76. 如图, ,且点A、B的坐标分别为 ,则 长是( )
A、2 B、3 C、4 D、76. 如图, ,且点A、B的坐标分别为 ,则 长是( )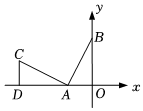 A、 B、5 C、4 D、37. 如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,∠ACB=25°,则∠ADC的度数是( )
A、 B、5 C、4 D、37. 如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,∠ACB=25°,则∠ADC的度数是( ) A、45° B、60° C、75° D、70°8. 如图,△ABC≌△ADE,∠C=40°,则∠E的度数为( )
A、45° B、60° C、75° D、70°8. 如图,△ABC≌△ADE,∠C=40°,则∠E的度数为( ) A、80° B、75° C、40° D、70°9. 如图,点D,E,F分别在的边 , , 上(不与顶点重合),设 , .若 , 则 , 满足的关系是( )
A、80° B、75° C、40° D、70°9. 如图,点D,E,F分别在的边 , , 上(不与顶点重合),设 , .若 , 则 , 满足的关系是( ) A、 B、 C、 D、10. 如图,四边形中, , , 我们把这种两组邻边分别相等的四边形叫做“筝形”.下列关于筝形的结论正确的是( )
A、 B、 C、 D、10. 如图,四边形中, , , 我们把这种两组邻边分别相等的四边形叫做“筝形”.下列关于筝形的结论正确的是( ) A、对角线AC,BD互相垂直平分 B、对角线BD平分∠ABC,∠ADC C、直线AC,BD是筝形的两条对称轴 D、筝形的面积等于对角线AC与BD的乘积
A、对角线AC,BD互相垂直平分 B、对角线BD平分∠ABC,∠ADC C、直线AC,BD是筝形的两条对称轴 D、筝形的面积等于对角线AC与BD的乘积二、填空题
-
11. 如果两个图形全等,那么它们的面积.12. 如图所示的图案是由全等的图形拼成的,其中AD=0.5,BC=1,则AF=.
 13. 三国时期,数学家赵爽绘制了“勾股圆方图”,又叫“赵爽弦图”,如图所示,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和四边形EFGH都是正方形,如果EF=2,AH=6,那么四边形ABCD的面积等于.
13. 三国时期,数学家赵爽绘制了“勾股圆方图”,又叫“赵爽弦图”,如图所示,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和四边形EFGH都是正方形,如果EF=2,AH=6,那么四边形ABCD的面积等于.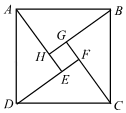 14. 如图,△ABC≌△DEF,BE=5,BF=1,则CF=.
14. 如图,△ABC≌△DEF,BE=5,BF=1,则CF=.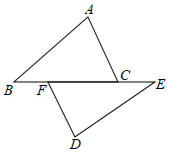 15. 若 , A与D,B与E分别是对应顶点, , , 则.16. 在平面直角坐标系中,已知 , , , 若 , 则点D的坐标为.17. 如图,△ABC≌△DEF,若∠A=65° ,则∠EDC的度数为.
15. 若 , A与D,B与E分别是对应顶点, , , 则.16. 在平面直角坐标系中,已知 , , , 若 , 则点D的坐标为.17. 如图,△ABC≌△DEF,若∠A=65° ,则∠EDC的度数为. 18. 如图,在平面直角坐标系xOy中,点A(2,0),B(4,2),若点P在x轴下方,且以O,A,P为顶点的三角形与OAB全等,则满足条件的P点的坐标是 .
18. 如图,在平面直角坐标系xOy中,点A(2,0),B(4,2),若点P在x轴下方,且以O,A,P为顶点的三角形与OAB全等,则满足条件的P点的坐标是 .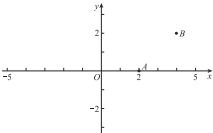 19. 如图是两个全等的三角形,图中字母表示三角形的边长,则∠的度数为°.
19. 如图是两个全等的三角形,图中字母表示三角形的边长,则∠的度数为°. 20. 如图,在平面直角坐标系xOy中,点A(-3,0),B(3,0),C(3,2),如果△ABC与△ABD全等,那么点D的坐标可以是(写出一个即可).
20. 如图,在平面直角坐标系xOy中,点A(-3,0),B(3,0),C(3,2),如果△ABC与△ABD全等,那么点D的坐标可以是(写出一个即可).
三、作图题
-
21. 沿着图中的虚线,用四种不同的方法将下面的图形分成两个全等的图形

四、解答题
-
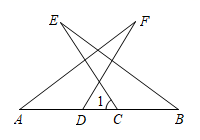
22. 如图, 中, 于点D, , , ,连接AF.线段AE与AF有怎样的关系?请写出你的猜想,并说明理由.
 23. 如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=CE.求证:AC∥DF.
23. 如图,已知点B、F、C、E在同一直线上,AB∥DE,AB=DE,BF=CE.求证:AC∥DF. 24. 如图,∠ABC=∠DCB,BD、CA分别平分∠ABC、∠DCB.求证:AC=DB.
24. 如图,∠ABC=∠DCB,BD、CA分别平分∠ABC、∠DCB.求证:AC=DB. 25. 图中所示的是两个全等的五边形,∠β=115°,d=5,指出它们的对应顶点•对应边与对应角,并说出图中标的a,b,c,e,α各字母所表示的值.
25. 图中所示的是两个全等的五边形,∠β=115°,d=5,指出它们的对应顶点•对应边与对应角,并说出图中标的a,b,c,e,α各字母所表示的值.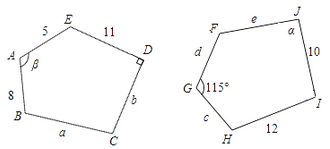
五、综合题
-
26. 如图①,已知直线y=﹣2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
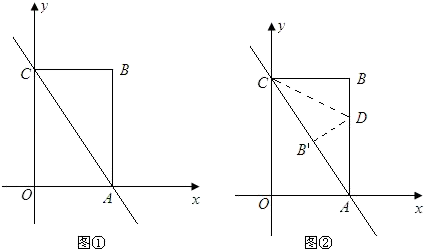 (1)、求点A、C的坐标;(2)、将△ABC对折,使得点A与点C重合,折痕交AB于点D,求直线CD的解析式(图②);(3)、在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)、求点A、C的坐标;(2)、将△ABC对折,使得点A与点C重合,折痕交AB于点D,求直线CD的解析式(图②);(3)、在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
-