江西省2022届高三理数5月高考适应性大练兵联考试卷
试卷更新日期:2022-07-04 类型:高考模拟
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 若复数z满足 , 则( )A、 B、 C、 D、3. 已知双曲线C:的一条渐近线方程为 , 则C的实轴长为( )A、1 B、2 C、 D、24. 2021年我国全国发电量累计值为81121.8亿千瓦时,相比2020年增长了6951.4亿千瓦时,如图是我国2020年和2021年全国发电结构占比图,则下列说法错误的是( )
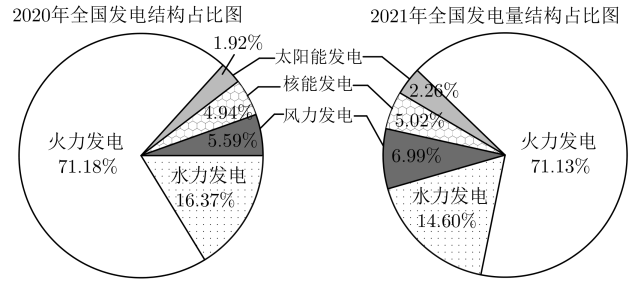 A、2020年与2021年这两年的全国发电量中火力发电占比均最高 B、2021年全国火力发电量低于2020年全国火力发电量 C、2020年与2021年的全国水力发电量占比均在当年排名第二 D、2021年的风力、太阳能、核能发电量占比均高于2020年5. 已知实数x,y满足不等式组 , 则的最小值是( )A、- B、-1 C、- D、-26. 函数的部分图象大致为( )A、
A、2020年与2021年这两年的全国发电量中火力发电占比均最高 B、2021年全国火力发电量低于2020年全国火力发电量 C、2020年与2021年的全国水力发电量占比均在当年排名第二 D、2021年的风力、太阳能、核能发电量占比均高于2020年5. 已知实数x,y满足不等式组 , 则的最小值是( )A、- B、-1 C、- D、-26. 函数的部分图象大致为( )A、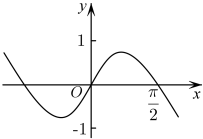 B、
B、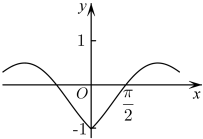 C、
C、 D、
D、 7. 如图,何尊是我国西周早期的青铜礼器,其造型浑厚,工艺精美,尊内底铸铭文中的“宅兹中国”为“中国”一词最早的文字记载,何尊还是第一个出现“德”字的器物,证明了周王朝以德治国的理念,何尊的形状可近似看作是圆台和圆柱的组合体,组合体的高约为 , 上口直径约为 , 经测量可知圆台的高约为 , 圆柱的底面直径约为 , 则该组合体的体积约为( )(其中的值取 , )
7. 如图,何尊是我国西周早期的青铜礼器,其造型浑厚,工艺精美,尊内底铸铭文中的“宅兹中国”为“中国”一词最早的文字记载,何尊还是第一个出现“德”字的器物,证明了周王朝以德治国的理念,何尊的形状可近似看作是圆台和圆柱的组合体,组合体的高约为 , 上口直径约为 , 经测量可知圆台的高约为 , 圆柱的底面直径约为 , 则该组合体的体积约为( )(其中的值取 , ) A、 B、 C、 D、8. 在正项等比数列中, , 则( )A、 B、 C、 D、9. 在△ABC中,内角A,B,C所对的边分别为a,b,c,且 , 则的值为( )A、4 B、5 C、6 D、710. 已知圆C的半径为2,点A满足 , E,F分别是C上两个动点,且 , 则的取值范围是( )A、[6,24] B、[4,22] C、[6,22] D、[4,24]11. 已知函数)有三个零点,则实数a的取值范围是( )A、(0,) B、(0,) C、(0,1) D、(0,e)12. 已知正方体的棱长为3,点P在的内部及其边界上运动,且 , 则点P的轨迹长度为( )A、 B、2π C、 D、3π
A、 B、 C、 D、8. 在正项等比数列中, , 则( )A、 B、 C、 D、9. 在△ABC中,内角A,B,C所对的边分别为a,b,c,且 , 则的值为( )A、4 B、5 C、6 D、710. 已知圆C的半径为2,点A满足 , E,F分别是C上两个动点,且 , 则的取值范围是( )A、[6,24] B、[4,22] C、[6,22] D、[4,24]11. 已知函数)有三个零点,则实数a的取值范围是( )A、(0,) B、(0,) C、(0,1) D、(0,e)12. 已知正方体的棱长为3,点P在的内部及其边界上运动,且 , 则点P的轨迹长度为( )A、 B、2π C、 D、3π二、填空题
-
13. 已知命题p:“ , ”为真命题,则实数a的最大值是 .14. 将函数的图像向左平移()个单位长度,得到函数g(x)的图像,若 , 则的最小值是 .15. 随着乡村的发展,很多乡村融合本地的特点发展旅游业,某县运用本地特点和风俗习惯打造了多个特色乡村,有4名游客打算去该县的A,B,C三个特色乡村旅游,每人只选择一个乡村旅游,则这4人恰好选择了两个乡村旅游的概率为 .16. 如图,椭圆M:的左、右焦点分别为 , , 两平行直线 , 分别过 , 交M于A,B、C,D四点,且 , , 则M的离心率为 .
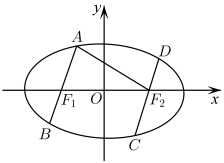
三、解答题
-
17. 在① , ②(b为常数),③这三个条件中选择一个,补充在下面横线中,并给出解答.
已知等差数列的前n项和为 , , 且____.
(1)、求的通项公式;(2)、求数列的前n项和 .注:如选择多个条件分别解答,按第一个解答计分.
18. 为迎接2022年9月在杭州举办的第19届亚运会,亚组委志愿者部对所有报名参加志愿者工作的人员进行了首场通用知识培训,并进行了通用知识培训在线测试,不合格者不得被录用,并在所有测试成绩中随机抽取了男、女各50名预录用志愿者的测试成绩(满分100分),将他们的成绩分为4组:[60,70),[70,80),[80,90),[90,100],整理得到如下频数分布表.成绩分
[60,70)
[70,80)
[80,90)
[90,100]
预录用男志愿者
15
5
15
15
预录用女志愿者
10
10
20
10
(1)、试从均值和方差的角度分析,样本成绩较好的是预录用男志愿者还是预录用女志愿者(同一组中的数据用该组区间的中点值作代表);(2)、将频率作为概率,现从所有预录用志愿者成绩在[80,90)的人中随机抽取4人试用,记其中男志愿者的人数为X,求X的数学期望与方差.19. 如图,在四棱锥P-ABCD中,底面ABCD为矩形,点E在棱AD上,且 , PE⊥底面ABCD, , . (1)、证明:;(2)、求平面PBE与平面PCD所成锐二面角的余弦值.20. 已知抛物线 , 动直线l经过点(2,5)交C于A,B两点,O为坐标原点,当l垂直于y轴时,△OAB的面积为10 .(1)、求C的方程;(2)、C上是否存在定点P,使得P在以AB为直径的圆上?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、证明:;(2)、求平面PBE与平面PCD所成锐二面角的余弦值.20. 已知抛物线 , 动直线l经过点(2,5)交C于A,B两点,O为坐标原点,当l垂直于y轴时,△OAB的面积为10 .(1)、求C的方程;(2)、C上是否存在定点P,使得P在以AB为直径的圆上?若存在,求出点P的坐标;若不存在,请说明理由.