福建省厦门市2022届高三毕业班数学第四次质量检测试卷

试卷更新日期：2022-07-04 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知函数 $f (x) = {\begin{array}{l} l o g_{2} x ， x \geq 1 \\ x^{2} - 1 ， x < 1 \end{array}$ ，则 $f (f (- 3)) =$ （）

A、0 B、1 C、2 D、3

查看试题解析
2. 已知集合M，N满足 $M ∩ N \neq \emptyset$ ，则（）

A、 $\forall x \in M ， x \in N$ B、 $\forall x \in M ， x \notin N$ C、 $\exists x \in M ， x \in N$ D、 $\exists x \in M ， x \notin N$

查看试题解析
3. 已知抛物线 $C ： y^{2} = 2 p x (p > 0)$ 的准线被圆 $x^{2} + y^{2} = 4$ 所截得的弦长为 $2 \sqrt{3}$ ，则 $p =$ （）

A、1 B、 $\sqrt{3}$ C、2 D、4

查看试题解析
4. 已知平面 $α ， β$ ，直线 $m ， n$ 满足 $α ⊥ β$ ， $α ∩ β = l$ ， $m ⊥ α$ ， $n / / β$ ，则（）

A、 $m / / β$ B、 $n ⊥ α$ C、 $n / / l$ D、 $m ⊥ l$

查看试题解析
5. 已知 $α ， β \in (0 ， π)$ ，且 $t a n α = \frac{c o s 2 β - 1}{s i n 2 β} = 2$ ，则 $c o s (α - β) =$ （）

A、 $- \frac{4}{5}$ B、 $- \frac{3}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
6. 我们将服从二项分布的随机变量称为二项随机变量，服从正态分布的随机变量称为正态随机变量．概率论中有一个重要的结论是棣莫弗一拉普拉斯极限定理，它表明，若随机变量 $Y \sim B (n ， p)$ ，当n充分大时，二项随机变量Y可以由正态随机变量X来近似，且正态随机变量X的期望和方差与二项随机变量Y的期望和方差相同．棣莫弗在1733年证明了 $p = \frac{1}{2}$ 的特殊情形，1812年，拉普拉斯对一般的p进行了证明．现抛掷一枚质地均匀的硬币100次，则利用正态分布近似估算硬币正面向上次数超过60次的概率为（）（附：若 $X ∼ N (μ ， σ^{2})$ ，则 $P (μ - σ \leq X \leq μ + σ) \approx 0.6827$ ， $P (μ - 2 σ \leq X \leq μ + 2 σ) \approx 0.9545$ ， $P (μ - 3 σ \leq X \leq μ + 3 σ) \approx 0.9973$ ）

A、0.1587 B、0.0228 C、0.0027 D、0.0014

查看试题解析
7. 已知 ${\vec{e}}_{1} ， {\vec{e}}_{2}$ 为单位向量，满足 $| {\vec{e}}_{1} - {\vec{e}}_{2} | = | 2 {\vec{e}}_{1} - \vec{a} | = 1$ ，则 $| \vec{a} - {\vec{e}}_{2} |$ 的最小值为（）

A、 $\sqrt{3} - 1$ B、 $\sqrt{3}$ C、 $\sqrt{7} - 1$ D、 $\sqrt{7}$

查看试题解析
8. 已知 $a = l o g_{b} c ， b = l o g_{c} a$ ，则（）

A、 $a < b < c$ B、 $b < c < a$ C、 $c < a < b$ D、 $c < b < a$

查看试题解析

二、多选题

9. 为推动学校体育运动发展，引导学生积极参与体育锻炼，增强健康管理意识，某校根据性别比例采用分层抽样方法随机抽取了120名男生和80名女生，调查并分别绘制出男、女生每天在校平均体育活动时间的频率分布直方图（如图所示），则（）

A、 $a = 0.010$ B、该校男生每天在校平均体育活动时间中位数的估计值为75 C、估计该校至少有一半学生每天在校平均体育活动时间超过一小时 D、估计该校每天在校平均体育活动时间不低于80分钟的学生中男、女生人数比例为 $9 ： 2$

查看试题解析
10. 已知正方形 $A B C D$ 的边长为1，以 $B D$ 为折痕把 $△ A B D$ 折起，得到四面体 $A^{'} B C D$ ，则（）

A、 $A^{'} C ⊥ B D$ B、四面体 $A^{'} B C D$ 体积的最大值为 $\frac{\sqrt{2}}{4}$ C、 $△ A^{'} C D$ 可以为等边三角形 D、 $△ A^{'} C D$ 可以为直角三角形

查看试题解析
11. 已知F为双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的右焦点，过F的直线l与圆 $O ： x^{2} + y^{2} = a^{2}$ 相切于点M，l与C及其渐近线在第二象限的交点分别为P，Q，则（）

A、 $| M F | = b$ B、直线 $O M$ 与C相交 C、若 $| M F | = \frac{1}{4} | Q F |$ ，则C的渐近线方程为 $y = \pm 2 x$ D、若 $| M F | = \frac{1}{4} | P F |$ ，则C的离心率为 $\frac{5}{3}$

查看试题解析
12. 已知函数 $f (x) = \frac{2^{x}}{4^{x} - 4} + \frac{x}{x - 1}$ ，则（）

A、 $f (x)$ 是奇函数 B、 $f (x)$ 的图象关于点 $(1 ， 1)$ 对称 C、 $f (x)$ 有唯一一个零点 D、不等式 $f (2 x + 3) > f (x^{2})$ 的解集为 $(- 1 ， 1) ∪ (3 ， + \infty)$

查看试题解析

三、填空题

13. 在复平面内，复数 $z = i (1 + m i) (m \in R)$ 对应的点位于直线 $y = x$ 上，则 $m =$ ．

查看试题解析
14. 已知函数 $f (x) = s i n (ω x + φ) (0 < φ < π)$ ，写出一个同时满足以下条件的 $ω$ 的值．
① $ω \in N^{*}$ ；
② $f (x)$ 是偶函数；
③ $f (x)$ 在 $(- \frac{π}{6} ， \frac{π}{3})$ 上恰有两个极值点．

查看试题解析
15. 为提升市民的艺术修养，丰富精神文化生活，市图书馆开设了工艺、绘画、雕塑等公益讲座，讲座海报如图所示．某人计划用三天时间参加三场不同类型讲座，则共有种选择方案．（用数字作答）

查看试题解析
16. 已知数列 ${\frac{n^{2}}{2 n - 1}}$ 与数列 ${\frac{n^{2}}{2 n + 1}}$ 的前n项和分别为 $S_{n} ， T_{n}$ ，则 $S_{5} - T_{5} =$ ；若 $S_{n} - T_{n} < λ (n + 1) (n + 16)$ 对于 $\forall n \in N^{*}$ 恒成立，则实数 $λ$ 的取值范围是．

查看试题解析

四、解答题

17. $△ A B C$ 的内角A，B，C的对边分别是a，b，c．已 $\sqrt{3} a s i n C - c c o s A = c$ ．

(1)、求A；

(2)、D为 $B C$ 的中点， $D E ⊥ A B$ ，垂足为E， $D F ⊥ A C$ ，垂足为F．若 $a = 2$ ，求 $△ D E F$ 面积的最大值．

查看试题解析
18. 如图，点 $O$ 是正方形 $A B C D$ 的中心， $C D ⊥ D E$ ， $C D / / E F$ ， $C D = 2 E F = 4$ ， $A C ⊥ O E$ ．

(1)、证明： $E D ⊥$ 平面 $A B C D$ ；

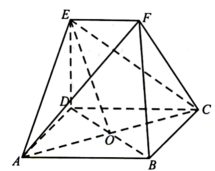(2)、若直线 $O E$ 与平面 $A B C D$ 所成角的正切值为 $\frac{\sqrt{2}}{2}$ ，求二面角 $E - A C - F$ 的余弦值．

查看试题解析
19. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，满足 $a_{1} = - 3$ ， $S_{n + 1} + 2 S_{n} + 3 n + 3 = 0$ ， $n \in N^{*}$ ．

(1)、证明：数列 ${a_{n} + 1}$ 是等比数列；

(2)、记 $m i n {a ， b} = {\begin{array}{l} a ， a \leq b \\ b ， a > b \end{array}$ ，设 $b_{n} = m i n {a_{n} ， n - 1}$ ，求数列 ${b_{n}}$ 的前 $2 n$ 项和 $T_{2 n}$ ．

查看试题解析
20. $△ A B C$ 中， $A (- 1 ， 0) ， B (1 ， 0) ， | A C | = 2 \sqrt{2}$ ，线段 $A C$ 上的点M满足 $∠ M B C = ∠ M C B$ ．

(1)、记M的轨迹为 $Γ$ ，求 $Γ$ 的方程；

(2)、过B的直线l与 $Γ$ 交于P，Q两点，且 $\vec{P B} = 3 \vec{B Q}$ ，判断点C和以 $P Q$ 为直径的圆的位置关系．

查看试题解析
21. 某工厂采购了一批新的生产设备．经统计，设备正常状态下，生产的产品正品率为0.98．为监控设备生产过程，检验员每天从该设备生产的产品中随机抽取10件产品，并检测质量．规定：抽检的10件产品中，若至少出现2件次品，则认为设备生产过程出现了异常情况，需对设备进行检测及修理．

(1)、假设设备正常状态，记X表示一天内抽取的10件产品中的次品件数，求 $P (X ≥ 2)$ ，并说明上述监控生产过程规定的合理性；

(2)、该设备由甲、乙两个部件构成，若两个部件同时出现故障，则设备停止运转；若只有一个部件出现故障，则设备出现异常．已知设备出现异常是由甲部件故障造成的概率为p，由乙部件故障造成的概率为 $1 - p$ ．若设备出现异常，需先检测其中一个部件，如果确认该部件出现故障，则进行修理，否则，继续对另一部件进行检测及修理．已知甲部件的检测费用1000元，修理费用5000元，乙部件的检测费用2000元，修理费用4000元．当设备出现异常时，仅考虑检测和修理总费用，应先检测甲部件还是乙部件，请说明理由．
参考数据： $0.9 8^{10} \approx 0.82 ， 0.9 8^{9} \approx 0.83 ， 0.9 8^{8} \approx 0.85$ ．

查看试题解析
22. 已知函数 $f (x) = (2 + s i n x + c o s x) e^{x} - a (x + s i n x) (a \in R)$ ．

(1)、讨论 $f (x)$ 的单调性；

(2)、当 $x \leq 0$ 时， $f (x) \geq 4 x + 3$ ，求 $a$ 的取值范围．

查看试题解析