江苏省淮安市金湖县2021-2022学年七年级下学期期末数学试卷
试卷更新日期:2022-07-04 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了0.000000022米.用科学记数法表示0.000000022为( )A、 B、 C、 D、3. 如图,直线l1∥l2 , ∠1=136°,则∠2的度数是( )
 A、44° B、46° C、54° D、64°4. 若一个三角形的两边长分别为3 cm和7 cm,则第三边长可能是( )A、6 cm B、3 cm C、2 cm D、11 cm5. 不等式2x+3>1的解集在数轴上表示正确的是( )A、
A、44° B、46° C、54° D、64°4. 若一个三角形的两边长分别为3 cm和7 cm,则第三边长可能是( )A、6 cm B、3 cm C、2 cm D、11 cm5. 不等式2x+3>1的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、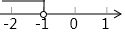 D、
D、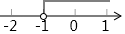 6. 下列命题为假命题的是( )A、若|a|=|b|,则a=b B、两直线平行,内错角相等, C、对顶角相等 D、若a=0,则ab=07. 已知 是二元一次方程 的一个解,则 的值为( )A、3 B、-5 C、-3 D、58. 如图,在△ABC中, , 点D在AB上,将△ABC沿CD折叠,点B落在边AC上的点E处,若 , 则∠A的度数为( )
6. 下列命题为假命题的是( )A、若|a|=|b|,则a=b B、两直线平行,内错角相等, C、对顶角相等 D、若a=0,则ab=07. 已知 是二元一次方程 的一个解,则 的值为( )A、3 B、-5 C、-3 D、58. 如图,在△ABC中, , 点D在AB上,将△ABC沿CD折叠,点B落在边AC上的点E处,若 , 则∠A的度数为( ) A、25° B、30° C、35° D、40°
A、25° B、30° C、35° D、40°二、填空题
-
9. 计算的结果是.10. 分解因式: .11. 已知一个多边形的每一个内角都等于150°,则这个多边形的边数是 .12. 二元一次方程2x+y=5的正整数解为 .13. 命题“三角形的三个内角中至少有两个锐角”是(填“真命题”或“假命题”).14. 如图,三角尺的直角顶点落在长方形纸片的一边上,若 , 则的度数是 .
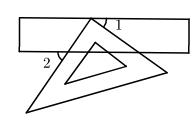 15. 已知 , 则.16. 如图, , E、F分别是AB、CD上的点,EH、FH分别是∠AEG和∠CFG的角平分线.若∠G=110°,则∠H=°.
15. 已知 , 则.16. 如图, , E、F分别是AB、CD上的点,EH、FH分别是∠AEG和∠CFG的角平分线.若∠G=110°,则∠H=°.
三、解答题
-
17. 计算:(1)、;(2)、.18.(1)、解方程组(2)、解不等式组19. 先化简,再求值: , 其中a=2,b=-1.20. 如图,在方格纸中,每个小正方形的边长都为1个单位长度.在方格纸内将△ABC经过平移后得到 , 、、分别是A、B、C的对应点,图中标出了点B的对应点.点A、B、C、均在方格纸的网格点上.
 (1)、补全;(2)、画出AC边上的中线BD;(3)、△ABD的面积为.21. 已知:如图, , ∠C+∠F=180°.求证:.
(1)、补全;(2)、画出AC边上的中线BD;(3)、△ABD的面积为.21. 已知:如图, , ∠C+∠F=180°.求证:. 22. 如图,在△ABC中,点D、E分别在AB、BC上,且DE∥AC,∠BDE=56°,∠C=52°,求∠B的度数.
22. 如图,在△ABC中,点D、E分别在AB、BC上,且DE∥AC,∠BDE=56°,∠C=52°,求∠B的度数. 23. 观察下列式子: , , ……(1)、请你根据上面式子的规律直接写出第7个式子:.(2)、探索以上式子的规律,试写出第n个等式(n为正整数),并说明你结论的正确性.24. 已知x+2y=5.(1)、请用含x的式子表示y;(2)、当时,求x的最大值.25. 某货运公司有大小两种货车,3辆大货车与4辆小货车一次可以运货29吨,2辆大货车与6辆小货车一次可以运货31吨.(1)、请问1辆大货车和1辆小货车一次可以分别运货多少吨;(2)、目前有46.4吨货物需要运输,货运公司拟安排大小货车共10辆,全部货物一次运完,其中每辆大货车一次运货花费500元,每辆小货车一次运货花费300元,请问货运公司应如何安排车辆最节省费用?最低费用为多少?26.(1)、学习“完全平方公式”时,小明遇到课本上一道题目“计算”,他联系所学过的知识和方法,想到两种解决思路:
23. 观察下列式子: , , ……(1)、请你根据上面式子的规律直接写出第7个式子:.(2)、探索以上式子的规律,试写出第n个等式(n为正整数),并说明你结论的正确性.24. 已知x+2y=5.(1)、请用含x的式子表示y;(2)、当时,求x的最大值.25. 某货运公司有大小两种货车,3辆大货车与4辆小货车一次可以运货29吨,2辆大货车与6辆小货车一次可以运货31吨.(1)、请问1辆大货车和1辆小货车一次可以分别运货多少吨;(2)、目前有46.4吨货物需要运输,货运公司拟安排大小货车共10辆,全部货物一次运完,其中每辆大货车一次运货花费500元,每辆小货车一次运货花费300元,请问货运公司应如何安排车辆最节省费用?最低费用为多少?26.(1)、学习“完全平方公式”时,小明遇到课本上一道题目“计算”,他联系所学过的知识和方法,想到两种解决思路:①可以用“整体思想”把三项式转化为两部分:或 , 然后可以利用完全平方公式解决,请你选择一种变形方法写出计算过程;
②可以用“数形结合”的方法,画出表示的图形,根据面积关系得到结果.请你在下面正方形中画出图形,并作适当标注;
 (2)、利用(1)的结论分解因式:;(3)、小明根据“任意一个实数的平方不小于0”,利用配方法求出了一些二次多项式的最大值或最小值,方法如下:
(2)、利用(1)的结论分解因式:;(3)、小明根据“任意一个实数的平方不小于0”,利用配方法求出了一些二次多项式的最大值或最小值,方法如下:①
∵
∴
故当x=3时代数式的最小值为-2.
②
∵
∴
故当x=-1时代数式的最大值为4.
请你综合以上表述,求当x,y满足什么条件时以下代数式有最小值,并确定它的最小值.
①;
②.
27. 【原题重现】例:如图1,AC、BD相交于点O,求证:∠A+∠B=∠C+∠D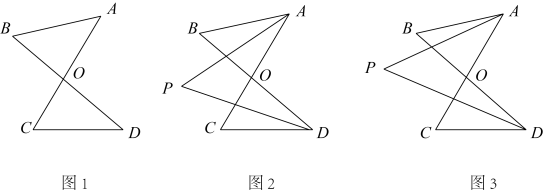
(1)、某数学兴趣小组同学对此题展开了探究讨论.【解法再探】课本利用“三角形内角和是180°”和“对顶角相等”对此题进行了证明,小明同学提出了另外一种证明方法,如下为思路框图:
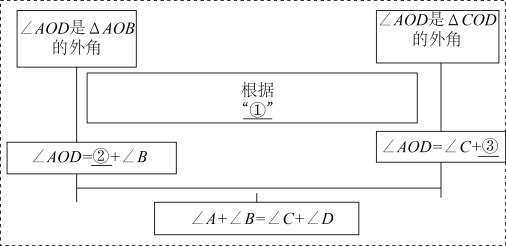
完成框图填空:① , ② , ③;
(2)、【变式拓展】小慧同学把图1中线段AC与BD相交所组成的结构称为“8字形”,她对原题进行了改编:如图2,AC、BD相交于点O , AP、DP分别是∠BAC和∠BDC内的一条射线,它们相交于点P , 请你根据(1)的结论写出关于∠P的两个关系式为:
①式∠P+∠BDP= , ②式∠P+∠CAP=;
小明进一步思考:若AP、DP分别是∠BAC和∠BDC的角平分线,由∠BAC+∠B=∠BDC+∠C , 得③式∠BAC-∠BDC=∠C-∠B , 由①式、③式(或②式、③式)联立、转化、整理可得∠P与∠B、∠C之间的关系,结论为:∠P=;(3)、【发现生成】小慧同学为了寻找规律,再次改变条件:如图3,AC、BD相交于点O , ∠BAP=∠BAC,∠BDP=∠BDC,探索∠P与∠B、∠C之间的关系.请你写出解答过程;(4)、若把(3)中的“”都改为“”,则∠P与∠B、∠C之间的关系为∠P=.