河南省开封市祥符区2021-2022学年七年级下学期期末考试数学试卷

试卷更新日期：2022-07-04 类型：期末考试

进入出卷网下载

一、单选题

1. 以下列各组线段为边，能组成三角形的是（）

A、 $4 c m ， 5 c m ， 6 c m$ B、 $2 c m ， 3 c m ， 5 c m$ C、 $3 c m ， 3 c m ， 6 c m$ D、 $5 c m ， 8 c m ， 2 c m$

查看试题解析
2. 维生素D缺乏与糖尿病的发生，发展存在相关性，维生素D对抑制肿瘤细胞增殖，诱导肿瘤细胞凋亡有一定作用，成人每天维生素D的摄人量约为0.0000046克.数据“0.0000046”用科学记数法表示为（）

A、 $46 \times 1 0^{- 7}$ B、 $4.6 \times 1 0^{- 6}$ C、 $4.6 \times 1 0^{- 7}$ D、 $0.46 \times 1 0^{- 6}$

查看试题解析
3. 下列事件是必然事件的是（）

A、打开电视，正在播新闻联播 B、某彩票的中奖率是1%，买100张一定能中奖 C、下届冬奥会谷爱凌一定能在自由式滑雪女子U型池比赛中夺得冠军 D、在只装有三个奖次奖票的奖箱中摸出一张，一定能中奖

查看试题解析
4. 下列计算正确的有（）个.

(1)、 $a^{3} \div a = a^{3}$ ，（2） $m^{2} \cdot m^{3} = m^{6}$ ，（3） $(a b^{2})^{2} = a^{2} b^{4}$ ，（4） ${(- x)}^{3} = - x^{3}$ ，

A、1 B、2 C、3 D、4

查看试题解析
5. 若 $(x + a) (x - 6)$ 展开式中不含有x的一次项，则a的值为（）

A、0 B、6 C、-6 D、6或-6

查看试题解析
6. 已知△ABC≌△A^'C^'B^' ， ∠B与∠C^' ， ∠C与∠B^'是对应角，有下列4个结论：①BC=C^'B^'；②AC=A^'B^'；③AB=A^'B^'；④∠ACB=∠A^'B^'C^' ，其中正确的结论有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，直线AB与直线CD相交于点O， $O E ⊥ A B$ ，且 $∠ B O D ： ∠ E O D = 1 ： 2$ ，则 $∠ E O C$ 的度数为（）

A、60° B、120° C、135° D、150°

查看试题解析
8. 如图所示的是一台自动测温记录仪的图象，它反映了祥符区夏季某天一段时间的气温T随时间t变化而变化的关系，观察图象得到的下列信息，其中错误的是（）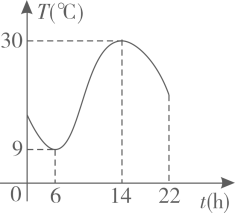

A、该段时间内最低气温为早上6点时的9℃ B、该段时间内14时气温最高是30℃ C、从0时至14时，气温随着时间的推移而上升 D、从14时至22时，气温随着时间的推移而下降

查看试题解析
9. 在 $△ A B C$ 中，分别以点A和B为圆心，以大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧交于点M、N；作直线MN，交BC于点D；连接AD.若 $△ A D C$ 的周长为12， $A B = 6$ ，则 $△ A B C$ 的周长为（）

A、6 B、12 C、18 D、24

查看试题解析

二、填空题

10. 计算： $4 x y \cdot (- 2 x y^{3})$ 的值为.

查看试题解析
11. 如图，若 $A D ∥ B E$ ，且 $A C ⊥ B C$ 于点C，若 $∠ C B E = 30 °$ ，则 $∠ C A D$ 的度数为.

查看试题解析
12. 一个长方形的周长为10cm，其中一条边长为 $x c m$ ，面积为 $y c m^{2}$ ，则y与x的关系式为.

查看试题解析
13. 如图，BO平分 $∠ A B C ， O D ⊥ B C$ 于点D，点E为射线BA上一动点，若 $O D = 5$ ，则OE的最小值为.

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ B A C = 80 ° ， A D ⊥ B C$ 于点D，AE平分 $∠ D A C ， ∠ B = 60 °$ ，则 $∠ D A E$ 的度数为.

查看试题解析

三、解答题

15. 计算：

(1)、 $2 a (a + 1) - 2 (a - 1) (a + 2)$

(2)、 ${(2 x - y)}^{2} - 4 (x - y) (x + y)$

查看试题解析
16. 先化简，再求值： $[(x y + 2) (x y - 2) - 2 x^{2} y^{2} + 4] \div x y$ ，其中 $x = 10$ ， $y = - \frac{1}{25}$ .

查看试题解析
17. 如图，已知 $∠ B = ∠ C ， A E ∥ B C$ ，那么AE平分 $∠ C A D$ 吗?请说明理由.

查看试题解析
18. 人的大脑所能记忆的内容是有限的，随着时间的推移，记忆的内容逐渐被遗忘.德国心理学家艾宾浩威斯第一个发现了记忆遗忘规律，他根据自己研究得到的测试数据描绘了一条曲线（如图所示），这就是著名的艾宾浩威斯遗忘曲线，其中纵轴表示学习中的记忆保持量，横轴表示时间.观察图象并回答下列问题：

(1)、学习后2h的时候，记忆保持量约是多少?

(2)、图中A点表示的实际意义是什么?在哪个时间段内遗忘的速度最快?

(3)、有研究表明，如及时复习，一天后能保持98%.根据遗忘曲线，如不复习，会有什么样的结果?小明说学习中能记住不过一会就忘了，都是因为自己笨.你同意他这样的说法吗?你会给他提出什么建议?

查看试题解析
19. 如图，对于给定的转盘，指针停在各个数字部分的概率都相等.小明和小亮两人做游戏，如果指针停在偶数，则小明赢；如果指针停在3的倍数，则小亮赢，那么这个游戏对小明和小亮公平吗?谁获胜的概率大?若不公平，你能修改游戏规则，使之公平吗?

查看试题解析
20. 如图，在正方形网格上有一个 $△ A B C$ .

⑴作 $△ A B C$ 关于直线 $E F$ 的轴对称图形；

⑵作 $△ A B C$ 的 $B C$ 边上的高 $A H$ ；

⑶若网格上的最小正方形边长为1，求 $△ A B C$ 的面积.

查看试题解析
21. 如图，在 $△ A B C$ 中， $A B = A C ， ∠ B A C = 90 °$ ，分别过B、C两点向经过点A的直线EF作垂线，垂足为点E、F.

(1)、BE与 $A F 、 C F$ 与AE分别相等吗?说明理由.

(2)、写出三条线段 $B E 、 C F 、 E F$ 之间的数量关系并说明理由.

查看试题解析
22. 如图

(1)、如图①，点D为等边 $△ A B C$ 边BC上一动点，以AD为边作等边 $△ A D E$ ，连接CE，猜想；BD与CE的数量关系是：； $∠ B$ 与 $∠ A C E$ 的数量关系是：

(2)、如图② $△ A B C$ 与 $△ A D E$ 均为等腰直角三角形， $∠ B A C = ∠ D A E = 90 °$ ，点D为边BC上一动点，
①试说明（1）中的两个结论是否仍然成立，若成立，写出证明的过程；若不成立，说明理由
②若 $B C = 6$ ，请直接写出点A到直线CE的距离.

查看试题解析