贵州省长顺县2021-2022学年七年级下学期阶段综合练习（四）数学试卷

试卷更新日期：2022-07-04 类型：月考试卷

进入出卷网下载

一、单选题

1. 北京2022年冬奥会会徽以汉字“冬”为灵感来源，图形上半部分展现滑冰运动员的造型，下半部分表现滑雪运动员的英姿.如图，下列选项中，可以由平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 9的算术平方根是（）

A、 81 B、3 C、±3 D、-3

查看试题解析
3. 在平面直角坐标系xOy中，点A（﹣1， $\sqrt{2}$ ）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 若 $a > b$ ，则下列不等式变形正确的是（）

A、 $- a + 7 < - b + 7$ B、 $\frac{a}{3} < \frac{b}{3}$ C、 $- 5 a > - 5 b$ D、 $2 a - 10 < 2 b - 10$

查看试题解析
5. 如图，射线OC的端点O在直线AB上，∠AOC的度数比∠BOC的2倍多10度.设∠AOC和∠BOC的度数分别为x，y，则下列正确的方程组为（）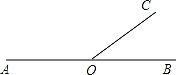

A、 ${\begin{array}{l} x + y = 180 \\ x = y + 10 \end{array}$ B、 ${\begin{array}{l} x + y = 180 \\ x = 2 y + 10 \end{array}$ C、 ${\begin{array}{l} x + y = 180 \\ x = 10 - 2 y \end{array}$ D、 ${\begin{array}{l} x + y = 180 \\ y = 2 x - 10 \end{array}$

查看试题解析
6. 为了了解某校九年级300名学生的体重情况，从中抽取50名学生的体重进行分析，在这项调查中，样本是指（）

A、300名学生 B、300名学生的体重 C、被抽取的50名学生 D、被抽取的50名学生的体重

查看试题解析
7. 已知 ${\begin{array}{l} x + 2 y = - 3 \\ 2 x + y = 7 \end{array}$ ，则代数式 $x - y$ 的值为（）

A、4 B、-4 C、-10 D、10

查看试题解析
8. 下列命题为真命题的是（）

A、两条直线被第三条直线所截，同位角相等 B、平移不改变图形的形状和大小 C、 $\sqrt{81}$ 的算术平方根是9 D、点 $(1 ， - a^{2})$ 一定在第四象限

查看试题解析
9. 在平面直角坐标系中，点A（﹣3，5）向右平移4个单位，再向下平移2个单位后的点的坐标是（）

A、（﹣3，3） B、（﹣3，7） C、（1，3） D、（﹣7，3）

查看试题解析
10. 下列调查中，最适合采用全面调查的是（）

A、疫情防控阶段进出某小区人员的体温检测 B、调查怀化市七年级学生的身高 C、检测一批手持测温仪的使用寿命 D、端午节期间市场上粽子质量

查看试题解析
11. 若不等式组 ${\begin{array}{l} x > a \\ x < 2 \end{array}$ 恰有3个整数解，则 $a$ 的取值范围是（）

A、 $a \leq 1$ B、 $a < - 1$ C、 $- 2 < a \leq - 1$ D、 $- 2 \leq a < - 1$

查看试题解析
12. 图（1）表示的是某书店今年1~4月的各月营业总额的情况，图（2）表示的是该书店“党史”类书籍的各月营业额占书店当月营业总额的百分比情况.若该书店1~4月的营业额一共是130万元，则这四个月中“党史”类书籍的营业额最高的是（）

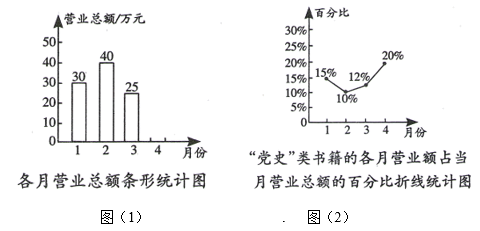A、1月 B、2月 C、3月 D、4月

查看试题解析

二、填空题

13. 已知 $| a + 4 |$ 和 $\sqrt{b - 3}$ 互为相反数，那么 $a + 3 b$ 等于.

查看试题解析
14. 某校200名学生一次数学测试的分数均大于75且小于150，分数段的频数分布情况如下： $75 ~ 90$ 有15人， $90 ~ 105$ 有42人， $105 ~ 120$ 有58人， $135 ~ 150$ 有35人（其中每个分数段可包括最小值，不包括最大值），那么测试分数在 $120 ~ 135$ 分数段的频数是.

查看试题解析
15. 一部电梯的额定限载量为1000千克，两人要用电梯把一批重物从底层搬到顶层，这两个人的身体重量分别为60千克和80千克，每箱货物质量为50千克，问他们每次最多只能搬运多少箱重物？（注：两个人都必须进入电梯）设每次能搬运x箱，则可列不等式为：.

查看试题解析
16. 对于实数 $a ， b (b \neq 0)$ ，定义运算“ $\oplus$ ”如下： $a \oplus b = (1 - a) \div b$ .例如： $3 \oplus 2 = (1 - 3) \div 2 = - 1$ ，则不等式 $x \oplus 2 \leq 3$ 的解集为.

查看试题解析

三、解答题

17.

(1)、计算： $(- 2)^{2} - | \sqrt{3} - 2 | - \sqrt{3^{2}} - \sqrt[3]{8}$ ；

(2)、已知 $(x - 3)^{2} = 4$ ，求x的值.

查看试题解析
18. 解方程组：

(1)、 ${\begin{array}{l} 2 x + y = 5 \\ x - y = 1 \end{array}$ ；

(2)、 ${\begin{array}{l} x - 2 y = 2 \\ \frac{x}{2} + \frac{y}{3} = 1 \end{array}$ .

查看试题解析
19. 解不等式组 ${\begin{array}{l} 2 (x - 1) + 3 \leq 7 \\ \frac{2 x + 5}{3} \geq 1 \end{array}$ ，并把解集在数轴上表示出来.

查看试题解析
20. 已知三角形 $A B C$ 的顶点分别为 $A (- 4 ， - 1)$ ， $B (- 5 ， - 4)$ ， $C (- 1 ， - 3)$ ，三角形 $A^{'} B^{'} C^{'}$ 是三角形 $A B C$ 经过平移得到的，三角形 $A B C$ 中任意一点 $P (x ， y)$ 平移后的对应点为 $P^{'} (x + 6 ， y + 4)$ .

(1)、写出点 $A^{'} ， C^{'}$ 的坐标；

(2)、请在图中建立直角坐标系，求三角形 $A^{'} B^{'} C^{'}$ 的面积.

查看试题解析
21. 某中学开展“阳光体育一小时”活动，根据学校实际情况，决定开设 $A ：$ 踢毽子； $B$ ：篮球； $C$ ：跳绳； $D$ ：健美操四种运动项目.为了了解学生最喜欢哪一种运动项目，随机抽取了一部分学生进行调查（每个被调查的同学必须在以上体育活动中选择一种），并将调查结果绘制成如下两幅不完整统计图.请结合图中的信息解答下列问题：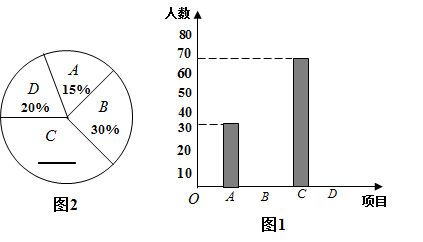

(1)、本次共调查了多少名学生？

(2)、请补全条形统计图，并求出扇形统计图中C部分所对应的扇形圆心角的度数；

(3)、若该中学有1200名学生，喜欢篮球运动项目的学生约有多少名？

查看试题解析
22. 《九章算术》中有这样一道题，原文如下：“今有人共买鸡，人出九，盈十一，人出六，不是十六，问人数、鸡价各几何”意思为：有几个人共同出钱买鸡，每人出九钱，则多了十一钱；每人出六钱，则少了十六钱，那么有几个人共同买鸡？鸡的价钱是多少？请解答上述问题.

查看试题解析
23.

(1)、阅读理解“ $| a |$ ”的几何意义是：数 $a$ 在数轴上对应的点到原点的距离，所以“ $| a | \geq 2$ ”可理解为：数 $a$ 在数轴上对应的点到原点的距离不小于2，则：
①“ $| a | < 2$ ”可理解为；
②请列举两个符号不同的整数，使不等式“ $| a | > 2$ ”成立，列举的 $a$ 的值为.
我们定义：形如“ $| x | \leq m ， | x | \geq m ， | x | < m ， | x | > m$ ”（ $m$ 为非负数）的不等式叫做绝对值不等式，能使一个绝对值不等式成立的所有未知数的值称为绝对值不等式的解集.

(2)、理解应用：根据绝对值的几何意义可以解一些绝对值不等式.

由上图可以得出：绝对值不等式 $| x | > 1$ 的解集是 $x < - 1$ 或 $x > 1$ ，绝对值不等式 $| x | \leq 3$ 的解集是 $- 3 ≤ x ≤ 3$ .则：

①不等式 $| x | \geq 4$ 的解集是.

②不等式 $| \frac{1}{2} x | < 2$ 的解集是.

查看试题解析
24. “低碳生活，绿色出行”已逐渐被大多数人所接受，某自行车专卖店有 $A$ ， $B$ 两种规格的自行车， $A$ 型车的利润为 $a$ 元/辆， $B$ 型车的利润为 $b$ 元/辆，该专卖店十月份前两周销售情况如下：

$A$ 型车销售量（辆）
$B$ 型车销售量（辆）
总利润（元）
第一周
10
12
2240
第二周
20
15
3400

(1)、求 $a$ ， $b$ 的值；

(2)、若第三周售出 $A$ ， $B$ 两种规格自行车共25辆，其中 $B$ 型车的销售量大于 $A$ 型车的售量，且不超过 $A$ 型车销售量的2倍，该专卖店售出 $A$ 型、 $B$ 型车各多少辆才能使第三周利润最大，最大利润是多少元？

查看试题解析
25. 实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图①，一束光线 $m$ 射到平面镜 $a$ 上，被 $a$ 反射后的光线为 $n$ ，则入射光线 $m$ ，反射光线 $n$ 与平面镜 $a$ 所夹的锐角 $∠ 1 = ∠ 2$ .

(1)、如图②，一束光线 $m$ 射到平面镜 $a$ 上，被 $a$ 反射到平面镜 $b$ 上，又被 $b$ 反射.若被 $b$ 反射出的光线 $n$ 与光线 $m$ 平行，且 $∠ 1 = 50 °$ ，则 $∠ 2 =$ ， $∠ 3 =$ .

(2)、在（1）中 $m ∥ n$ ，若 $∠ 1 = 55 °$ ，则 $∠ 3 =$ ；若 $∠ 1 = 40 °$ ，则 $∠ 3 =$ .

(3)、由（1），（2），请你猜想：当两平面镜 $a ， b$ 的夹角 $∠ 3 =$ ▲ 时，可以使任何射到平面镜 $a$ 上的光线 $m$ ，经过平面镜 $a ， b$ 的两次反射后，入射光线 $m$ 与反射光线 $n$ 平行.你能说明理由吗？

查看试题解析

	$A$ 型车销售量（辆）	$B$ 型车销售量（辆）	总利润（元）
第一周	10	12	2240
第二周	20	15	3400