江苏省盐城市2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-07-04 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图案中既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列分式中，是最简分式的是（）

A、 $\frac{m - 1}{1 - m}$ B、 $\frac{x - y}{x^{2} + y^{2}}$ C、 $\frac{x y - y}{3 x y}$ D、 $\frac{7 m}{5 m}$

查看试题解析
3. 下列根式中，与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{18}$ C、 $\sqrt[3]{6}$ D、 $\sqrt{\frac{2}{3}}$

查看试题解析
4. 反比例函数 $y = \frac{k}{x}$ 的图象经过点（3，2），则下列说法错误的是（）

A、 $k = 6$ B、函数图象分布在第一、三象限 C、y随x的增大而减小 D、当 $x > 0$ 时，y随x的增大而减小

查看试题解析
5. 若 $x = 4$ 是分式方程 $\frac{a - 2}{x} = \frac{1}{x - 3}$ 的根，则a的值为（）

A、3 B、4 C、5 D、6

查看试题解析
6. 如图，D、E、F是△ABC各边的中点，若△ABC的周长为12，则△DEF的周长为（）

A、2 B、4 C、6 D、8

查看试题解析
7. 如图，四边形 $A B C D$ 的两条对角线相交于点 $O$ ，且互相平分.添加下列条件，仍不能判定四边形 $A B C D$ 为菱形的是（）

A、 $A C ⊥ B D$ B、 $A B = A D$ C、 $A C = B D$ D、 $∠ A B D = ∠ C B D$

查看试题解析
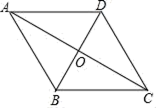8. 甲、乙两超市在1-5月间的盈利情况统计图如图所示，下列结论正确的是（）

A、甲超市的利润逐月减少 B、乙超市在6月份的利润必然超过甲超市 C、乙超市的利润逐月增加 D、3月份两家超市利润相同

查看试题解析

二、填空题

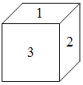
9. 要使式子 $\sqrt{x + 5}$ 有意义，则x的取值范围是．

查看试题解析
10. 计算： $(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})$ =.

查看试题解析
11. 直角三角形的两条直角边长分别为 $\sqrt{2}$ 、 $\sqrt{6}$ ，则这个直角三角形的面积为.

查看试题解析
12. 近年来食品安全问题备受人们的关注，某海关想检验一批进口食品的防腐剂含量是否符合国家标准，这种调查适用.（填“全面调查”或“抽样调查”）

查看试题解析
13. 已知一个菱形的边长为 $5$ ，其中一条对角线长为 $8$ ，则这个菱形的面积为.

查看试题解析
14. 如图，质地均匀的小立方体的一个面上标有数字1，两个面上标有数字2，三个面上标有数字3，抛掷这个小立方体，则向上一面的数字可能性最大的是.

查看试题解析
15. 如图，过四边形ABCD的四个顶点分别作对角线AC、BD的平行线，若所围成的四边形EFGH是矩形，则原四边形ABCD需满足的条件是.（只需写出一个符合要求的条件）

查看试题解析
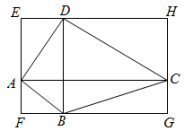16. 一次函出 $y = x + b$ （b为常数）的图象与x轴交于点A，与y轴交于点B，与反比例函 $y = \frac{4}{x}$ 的图象交于点C、D，点C在第一象限，点D在第三象限，若 $A C + B D = 2 \sqrt{2}$ ，则b＝.

查看试题解析

三、解答题

17. 解方程： $\frac{x}{2 x - 1} = 2 - \frac{3}{1 - 2 x}$

查看试题解析
18. 先化简，再求值 $\frac{1}{x - 1} + \frac{x^{2} - 3 x}{x^{2} - 1}$ ，其中 $x = \frac{1}{2}$ .

查看试题解析
19. 如图，一次函数y₁=kx+b（k≠0）的图象与反比侧函数y₂= $\frac{m}{x}$ （m≠0）的图象相交于点A（-3，2），B（n，- $\frac{3}{2}$ ）.

(1)、求一次函数和反比例函数的表达式；

(2)、请直接写出当 $y_{1} > y_{2}$ 时，x的取值范围.

查看试题解析
20. 如图，将平行四边形ABCD沿着对角线BD折叠，点C的对应点为C′，BC′与AD相交于点E.

(1)、 EB与ED相等吗？证明你的结论；

(2)、连接AC′，判断AC′与BD的位置关系，并说明理由.

查看试题解析
21. 某学校为了解八年级学生课外阅读情况，调查了该年级部分学生一周的课外阅读时间.并将结果绘制成如图所示的两幅不完整的统计图表，请你根据统计图表的信息回答下列问题：
抽取的学生课外阅读时间统计表
类别
阅读时间 $t$ （小时）
人数
$A$
$0 \leq t < 1$
2
$B$
$1 \leq t < 2$
4
$C$
$2 \leq t < 3$
4
$D$
$3 \leq t < 4$
$E$
$4 \leq t < 5$
13
$F$
$5 \leq t < 6$
$G$
$6 \leq t < 7$
7
抽取的学生课外阅读时间扇形统计图

(1)、本次共调查了名学生；

(2)、在扇形统计图中，类别为F的扇形圆心角的度数为；

(3)、若该年级共有1200名学生，请估算一周内阅读时间不少于4小时的人数.

查看试题解析
22. 如图1，在边长为4的正方形ABCD中，点E为对角线BD上一点，连接AE，过点E作 $E F ⊥ A E$ ，交边CD于点F，若 $D F = 2$ ，求BE的长.
下面是小明、小华和小东三位同学关于本题不同视角下的部分思维过程：

小明：从直线BD是正方形的对称轴角度看，连接EC，如图2，则 $E A = E C$ ， ∠ECD＝∠EAD，又 $∠ A D C = ∠ A E F = 9 0^{∘}$ ， ……

小华：从 $E F ⊥ A E$ 的角度看，可以过点E作BC的平行线，交AB、CD于M、N，如图3，通过证明 $△ A M E ≅ △ E N F$ ， ……

小东：从 $E F ⊥ A E$ 的角度看，还可以过点E作BD的垂线，交DC的延长线于点P，如图4，……

请结合上面的思路，求BE的长.

查看试题解析
23. 王老师驾驶小汽车从A地行驶到B地，行驶里程为480千米，设小汽车的行驶时间为t（单位：小时），行驶的平均速度为v（单位：千米/小时），且全程速度限定为不超过120千米/小时.

(1)、求v关于t的函数表达式；

(2)、王老师上午8点驾驶小汽车从A地出发.
①王老师需要在当天13点至14点（含13点和14点）间到达B地，求小汽车行驶的平均速度v需达到的范围；
②王老师能否在当天11点30分前到达B地？说明理由.

查看试题解析
24. 定义：对角线相等且所夹锐角为60°的四边形叫“60°等角线四边形”.
如图1，四边形ABCD为“60°等角线四边形”，即AC＝BD，∠AOB＝60°.
判定探究：

(1)、下列语句能判断四边形是“60°等角线四边形”的是.（填序号）
①对角线所夹锐角为60°的平行四边形；
②对角线所夹锐角为60°的矩形；
③对角线所夹锐角为60°，且顺次连接各边中点所形成的四边形是菱形的四边形.

(2)、性质探究：以AC为边，向下构造等边三角形△ACE，连接BE，如图2，请直接写出AB＋CD与AC的大小关系；

(3)、请判断AD＋BC与 $\sqrt{3}$ AC的大小关系，并说明理由；

(4)、学习应用：若“60°等角线四边形”的对角线长为4，则该四边形周长的最小值为.

查看试题解析
25. 如图，点M（0，m）为y轴上一点，m＜0，过点M作y轴的垂线l，与反比例函数 $y = \frac{1}{x}$ 的图象交于点P.把直线l下方反比例函数的图象沿着直线l翻折，其它部分保持不变，所形成的新图象称为“G图象”.

(1)、当m＝－1时，求“G图象”与x轴交点横坐标；

(2)、过y轴上另一点N（0，n）作y轴垂线，与“G图象”交于点A、B.
①若n＝2，且AN＝2BN，求m的值；
②若AN＝2BN，求m与n的数量关系.

查看试题解析

类别	阅读时间 $t$ （小时）	人数
$A$	$0 \leq t < 1$	2
$B$	$1 \leq t < 2$	4
$C$	$2 \leq t < 3$	4
$D$	$3 \leq t < 4$
$E$	$4 \leq t < 5$	13
$F$	$5 \leq t < 6$
$G$	$6 \leq t < 7$	7