江苏省连云港市海州区2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-07-04 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
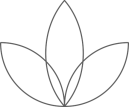 B、
B、 C、
C、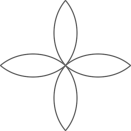 D、
D、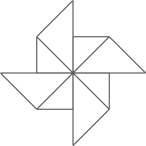 2. “明天连云港会下雨”,这个事件是( )A、必然事件 B、随机事件 C、不可能事件 D、确定事件3. 下列计算正确的是( )A、 + =2 B、3+ =3 C、 + = D、 + =3+4. 在下列命题中,正确的是( )A、有一组对边平行的四边形是平行四边形 B、有一组邻边相等的平行四边形是菱形 C、有一个角是直角的四边形是矩形 D、对角线互相垂直平分的四边形是正方形5. 在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其它差别,任意摸出一个球是红球的概率是( )A、 B、 C、 D、6. 如图,点在双曲线上,点在双曲线上,轴,则的面积等于( )
2. “明天连云港会下雨”,这个事件是( )A、必然事件 B、随机事件 C、不可能事件 D、确定事件3. 下列计算正确的是( )A、 + =2 B、3+ =3 C、 + = D、 + =3+4. 在下列命题中,正确的是( )A、有一组对边平行的四边形是平行四边形 B、有一组邻边相等的平行四边形是菱形 C、有一个角是直角的四边形是矩形 D、对角线互相垂直平分的四边形是正方形5. 在一个不透明的袋子中装有黑球m个、白球n个、红球3个,除颜色外无其它差别,任意摸出一个球是红球的概率是( )A、 B、 C、 D、6. 如图,点在双曲线上,点在双曲线上,轴,则的面积等于( )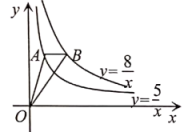 A、1.5 B、2 C、3 D、6.57. 有两个直角三角形纸板,一个含45°角,另一个含30°角,如图①所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A顺时针旋转,使BC∥DE , 如图②所示,则旋转角∠BAD的度数为( )
A、1.5 B、2 C、3 D、6.57. 有两个直角三角形纸板,一个含45°角,另一个含30°角,如图①所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A顺时针旋转,使BC∥DE , 如图②所示,则旋转角∠BAD的度数为( )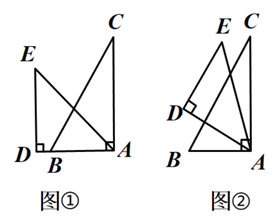 A、15° B、30° C、45° D、60°8. 两个反比例函数和在第一象限内的图象如图所示,点在的图象上,轴于点 , 交的图象于点 , 轴于点 , 交的图象于点 , 轴于点 , 当点在图象上运动时,以下结论:①与始终平行;②与始终相等;③四边形的面积不会发生变化;④的面积等于四边形的面积.其中一定正确的是( )
A、15° B、30° C、45° D、60°8. 两个反比例函数和在第一象限内的图象如图所示,点在的图象上,轴于点 , 交的图象于点 , 轴于点 , 交的图象于点 , 轴于点 , 当点在图象上运动时,以下结论:①与始终平行;②与始终相等;③四边形的面积不会发生变化;④的面积等于四边形的面积.其中一定正确的是( )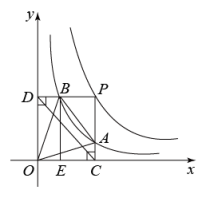 A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
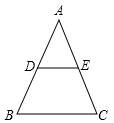
9. 若二次根式 有意义,则x的取值范围是 .10. 一个质地均匀的小正方体,6个面分别标有数字1,1,2,1,5,5,若随机投掷一次小正方体,则朝上一面的数字是1的概率为 .11. 如图所示,DE是△ABC的中位线,BC=8,则DE= .
 12. 已知在反比例函数图象的每个象限内,随增大而增大,则常数的取值范围是.13. 已知a、b为两个连续的整数,且 , 则a+b= .14. 一个菱形的周长为52cm,一条对角线长为10cm,则其面积为cm2.15. 若分式方程有增根,则.16. 如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为 .
12. 已知在反比例函数图象的每个象限内,随增大而增大,则常数的取值范围是.13. 已知a、b为两个连续的整数,且 , 则a+b= .14. 一个菱形的周长为52cm,一条对角线长为10cm,则其面积为cm2.15. 若分式方程有增根,则.16. 如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为 .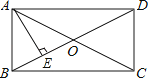 17. 如图,已知正方形 的边长为 ,点E是边 的中点,点P是对角线 上的动点,则 的最小值是.
17. 如图,已知正方形 的边长为 ,点E是边 的中点,点P是对角线 上的动点,则 的最小值是.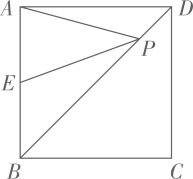 18. 如图,反比例函数的图象经过平行四边形的顶点 , , 若点、点、点的坐标分别为 , , , 且 , 则的值是.
18. 如图,反比例函数的图象经过平行四边形的顶点 , , 若点、点、点的坐标分别为 , , , 且 , 则的值是.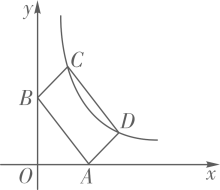
三、解答题
-
19. 计算与化简:(1)、化简(2)、化简(3)、计算(4)、计算20. 解分式方程:(1)、(2)、21. 某校为了解九年级学生体育测试情况,从九年级所有学生的体育测试成绩中随机抽取一部分学生的体育成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下不完整的统计图,请你结合图中所给信息解答下列问题:(说明:A级:40分~36分;B级:35分~32分;C级:31分~25分;D级:24分以下)
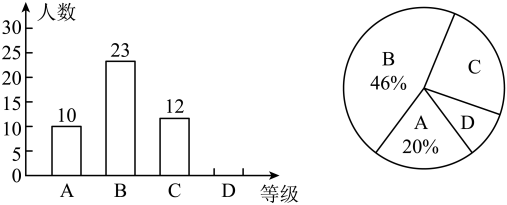 (1)、请将条形统计图补充完整;(2)、样本中D级的学生人数占抽取学生人数的百分比为;(3)、扇形统计图中C级所在的扇形圆心角为度:(4)、若该校九年级有1200名学生,请估计体育测试中A级学生人数约为多少人。22. 如图,在平面直角坐标系中,正比例函数y=3x与反比例函数y= 的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC.
(1)、请将条形统计图补充完整;(2)、样本中D级的学生人数占抽取学生人数的百分比为;(3)、扇形统计图中C级所在的扇形圆心角为度:(4)、若该校九年级有1200名学生,请估计体育测试中A级学生人数约为多少人。22. 如图,在平面直角坐标系中,正比例函数y=3x与反比例函数y= 的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC.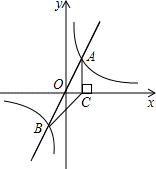 (1)、求反比例函数的表达式;(2)、求△ABC的面积;(3)、若点P是反比例函数y= 图象上的一点,△OPC与△ABC面积相等,请直接写出点P的坐标.23. 如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.
(1)、求反比例函数的表达式;(2)、求△ABC的面积;(3)、若点P是反比例函数y= 图象上的一点,△OPC与△ABC面积相等,请直接写出点P的坐标.23. 如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.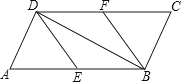 (1)、求证:△ADE≌△CBF(2)、若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.24. 某家电商场经销A种型号电视机,疫情结束后,五月份为刺激消费,购买A种型号电视机每台降价500元(享受政府补贴).如果卖出相同数量的A种型号电视机,疫情以前的销售额为5万元,如今的销售额减少1万元.(1)、如今A种型号电视机每台售价多少元?(2)、为了增加收入,电商公司决定再经销售价为5000元的B种型号电视机,五月份A、B两种型号电视机共销售85台,如果销售额不低于26万元,则B种型号电视机销售不低于多少台?25. 如图所示,制作一种产品的同时,需要将原材料加热,设该材料温度为 , 从加热开始计算的时间为分钟,据了解,该材料在加热过程中温度与时间成一次函数关系,已知该材料在加热前的温度为 , 加热5分钟使材料温度达到时停止加热.停止加热后,过一段时间,材料温度逐渐下降,这时温度与时间成反比例函数关系.
(1)、求证:△ADE≌△CBF(2)、若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.24. 某家电商场经销A种型号电视机,疫情结束后,五月份为刺激消费,购买A种型号电视机每台降价500元(享受政府补贴).如果卖出相同数量的A种型号电视机,疫情以前的销售额为5万元,如今的销售额减少1万元.(1)、如今A种型号电视机每台售价多少元?(2)、为了增加收入,电商公司决定再经销售价为5000元的B种型号电视机,五月份A、B两种型号电视机共销售85台,如果销售额不低于26万元,则B种型号电视机销售不低于多少台?25. 如图所示,制作一种产品的同时,需要将原材料加热,设该材料温度为 , 从加热开始计算的时间为分钟,据了解,该材料在加热过程中温度与时间成一次函数关系,已知该材料在加热前的温度为 , 加热5分钟使材料温度达到时停止加热.停止加热后,过一段时间,材料温度逐渐下降,这时温度与时间成反比例函数关系.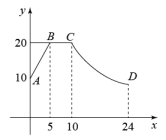 (1)、分别求出该材料加热过程中和材料温度逐渐下降过程中,与之间的函数表达式,并写出的取值范围;(2)、根据工艺要求,在材料温度不低于的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理所用的时间是多少?26. 如图,在平面直角坐标系中,四边形为正方形,已知点、 , 点、在第二象限内.
(1)、分别求出该材料加热过程中和材料温度逐渐下降过程中,与之间的函数表达式,并写出的取值范围;(2)、根据工艺要求,在材料温度不低于的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理所用的时间是多少?26. 如图,在平面直角坐标系中,四边形为正方形,已知点、 , 点、在第二象限内.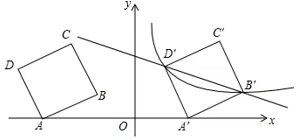 (1)、点的坐标;(2)、将正方形以每秒2个单位的速度沿轴向右平移秒,若存在某一时刻 , 使在第一象限内点、两点的对应点、正好落在某反比例函数的图象上,请求出此时的值以及这个反比例函数的解析式;(3)、在(2)的情况下,问是否存在轴上的点和反比例函数图象上的点 , 使得以、、、四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点的坐标;若不存在,请说明理由.27. 【问题情境】如图1,点为正方形内一点, , , , 将直角三角形绕点逆时针方向旋转度(),点、的对应点分别为点、.
(1)、点的坐标;(2)、将正方形以每秒2个单位的速度沿轴向右平移秒,若存在某一时刻 , 使在第一象限内点、两点的对应点、正好落在某反比例函数的图象上,请求出此时的值以及这个反比例函数的解析式;(3)、在(2)的情况下,问是否存在轴上的点和反比例函数图象上的点 , 使得以、、、四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点的坐标;若不存在,请说明理由.27. 【问题情境】如图1,点为正方形内一点, , , , 将直角三角形绕点逆时针方向旋转度(),点、的对应点分别为点、.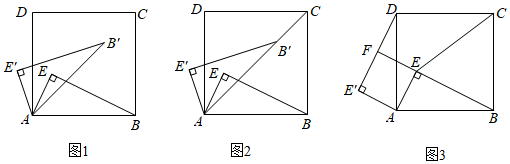 (1)、【问题解决】如图2,在旋转的过程中,点落在了上,求此时的长;(2)、【问题解决】若 , 如图3,得到(此时与重合),延长交于点 ,
(1)、【问题解决】如图2,在旋转的过程中,点落在了上,求此时的长;(2)、【问题解决】若 , 如图3,得到(此时与重合),延长交于点 ,①试判断四边形的形状,并说明理由;
②连接 , 求的长;
(3)、【问题解决】在直角三角形绕点逆时针方向旋转过程中,求线段长度的取值范围.