贵州省长顺县2021-2022学年八年级下学期阶段综合练习(四)数学试卷
试卷更新日期:2022-07-04 类型:月考试卷
一、单选题
-
1. 二次根式中,最简二次根式有( )A、1个 B、2个 C、3个 D、4个2. 二次根式 ,则a的取值范围是( )A、a≤2 B、a≤﹣2 C、a>2 D、a<03. 下列线段不能组成直角三角形的是( )A、3,4,5 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 三角形的三边为a、b、c,由下列条件不能判断它是直角三角形的是( ).A、 B、 C、 D、6. 在数学活动课上,老师要求同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的四位同学拟定的方案,其中正确的是( )A、测量对角线是否相互平分 B、测量两组对边是否分别相等 C、测量一组对角是否都为直角 D、测量四边形其中的三个角是否都为直角7. 在四边形中, , 不能判定四边形为矩形的是( )A、且 B、且 C、且 D、且8. 某居民今年1至6月份(共6个月)的月平均用水量5t,其中1至5月份月用水量(单位:t)统计如图所示,根据表中信息,该户今年1至6月份用水量的中位数和众数分别是( )
 A、4,5 B、4.5,6 C、5,6 D、5.5,69. 若正比例函数 的图象经过点O(a-1,4),则a的值为( )A、-1 B、0 C、1 D、210. 已知是一次函数的图象上三点,则的大小关系为( )A、 B、 C、 D、11. 能表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数且mn≠0)的图象的是( )A、
A、4,5 B、4.5,6 C、5,6 D、5.5,69. 若正比例函数 的图象经过点O(a-1,4),则a的值为( )A、-1 B、0 C、1 D、210. 已知是一次函数的图象上三点,则的大小关系为( )A、 B、 C、 D、11. 能表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数且mn≠0)的图象的是( )A、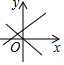 B、
B、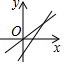 C、
C、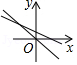 D、
D、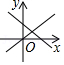 12. 如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )
12. 如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( ) A、1 B、1.3 C、1.2 D、1.5
A、1 B、1.3 C、1.2 D、1.5二、填空题
-
13. 四边形ABCD中,AD∥BC,AD=BC,对角线AC、BD相交于点O,若CD=3cm,△BOC的周长比△AOB的周长大2cm,则四边形ABCD的周长=cm.14. 一次函数y=ax+b与正比例函数y=kx在同一平面直角坐标系的图象如图所示,则关于x的不等式ax+b≥kx的解集为 .
 15. 如图,已知在 中, , ,分别以 , 为直径作半圆,面积分别记为 , ,则 + 的值等于 .
15. 如图,已知在 中, , ,分别以 , 为直径作半圆,面积分别记为 , ,则 + 的值等于 . 16. 在某项考核中,最终考核成绩(百分制)由研究性学习成绩与卷面成绩组成,其中研究性学习成绩占60%,卷面成绩占40%,小明的这两项成绩依次是90分和85分,则小明的最终考核成绩是分.
16. 在某项考核中,最终考核成绩(百分制)由研究性学习成绩与卷面成绩组成,其中研究性学习成绩占60%,卷面成绩占40%,小明的这两项成绩依次是90分和85分,则小明的最终考核成绩是分.三、解答题
-
17.(1)、计算:(2)、18. 如图,中, , , 是边上一点,且 , 若.求的长.
 19. 如图是由单位长度为1的小正方形组成的网格,按要求作图.
19. 如图是由单位长度为1的小正方形组成的网格,按要求作图. (1)、在图1中画出一条长为的线段;(2)、在图2中画出一个以格点(小正方形的顶点)为顶点,三边长都为无理数的直角三角形.20. 时代的到来将给人类生活带来巨大改变.现有两种型号的手机,进价和售价如下表所示:
(1)、在图1中画出一条长为的线段;(2)、在图2中画出一个以格点(小正方形的顶点)为顶点,三边长都为无理数的直角三角形.20. 时代的到来将给人类生活带来巨大改变.现有两种型号的手机,进价和售价如下表所示:
进价(元/部)
售价(元/部)
3000
3400
3500
4000
某营业厅购进两种型号手机共花费32000元.手机销售完成后共获得利润4400元.
(1)、营业厅购进两种型号手机各多少部?(2)、若营业厅再次购进两种型号手机共30部,其中型手机的数量不多于型手机数量的2倍,请设计一个方案:营业厅购进两种型号手机各多少部时获得最大利润,最大利润是多少?21. 为助力新冠肺炎疫情后经济的复苏,天天快餐公司积极投入到复工复产中.现有两家农副产品加工厂到该公司推销鸡腿,两家鸡腿的价格相同,品质相近.该公司决定通过检查质量来确定选购哪家的鸡腿.检察人员从两家分别抽取100个鸡腿,然后再从中随机各抽取10个,记录它们的质量(单位:克)如下:加工厂
74
75
75
75
73
77
78
72
76
75
加工厂
78
74
78
73
74
75
74
74
75
75
(1)、根据表中数据,求加工厂的10个鸡腿质量的中位数,平均数.(2)、根据鸡腿质量的稳定性,该快餐公司应选购哪家加工厂的鸡腿?22. 阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如: , 善于思考的小明进行了以下探索:设(其中均为整数),则有..这样小明就找到了一种把部分的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)、当均为正整数时,若 , 用含的式子分别表示 , 得 , ;(2)、若 , 且均为正整数,求的值.23. 如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2 , b1≠b2 , 那么称这两个一次函数为“平行一次函数”.已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=﹣2x+4是“平行一次函数”
(1)、若函数y=kx+b的图象过点(3,1),求b的值;(2)、若函数y=kx+b的图象与两坐标轴围成的面积是△AOB面积的 , 求y=kx+b的解析式.24. 如图,在梯形中, , 动点从点出发沿方向向点以的速度运动,动点从点开始沿着方向向点以的速度运动.点分别从点和点同时出发,当其中一点到达端点时,另一点随之停止运动. (1)、经过多长时间,四边形是平行四边形?(2)、经过多长时间,四边形是矩形?25. 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)、经过多长时间,四边形是平行四边形?(2)、经过多长时间,四边形是矩形?25. 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: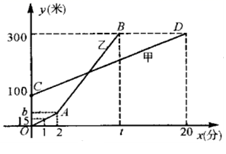 (1)、甲登山的速度是每分钟米,乙在A地提速时距地面的高度b为米.(2)、若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度y(米)与登山时间x(分)之间的函数关系式.(3)、登山多长时间时,乙追上了甲?此时乙距A地的高度为多少米?
(1)、甲登山的速度是每分钟米,乙在A地提速时距地面的高度b为米.(2)、若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度y(米)与登山时间x(分)之间的函数关系式.(3)、登山多长时间时,乙追上了甲?此时乙距A地的高度为多少米?