2022-2023学年浙教版数学八年级上册1.1 认识三角形 同步练习
试卷更新日期:2022-07-04 类型:同步测试
一、单选题
-
1. 已知三角形的两边长分别为2cm和3cm,则第三边长可能是( )A、6cm B、5cm C、3cm D、1cm2. 如图, 于点D, 于点C, 于点F,下列关于高的说法错误的是( )
 A、在 中, 是 边上的高 B、在 中, 是 边上的高 C、在 中, 是 边上的高 D、在 中, 是 边上的高3. 如图,直线l1、l2分别与△ABC的两边AB、BC相交,且l1∥l2 , 若∠B=35°,∠1=105°,则∠2的度数为( )
A、在 中, 是 边上的高 B、在 中, 是 边上的高 C、在 中, 是 边上的高 D、在 中, 是 边上的高3. 如图,直线l1、l2分别与△ABC的两边AB、BC相交,且l1∥l2 , 若∠B=35°,∠1=105°,则∠2的度数为( ) A、45° B、50° C、40° D、60°4. 三角形的内角和是( )A、60° B、90° C、180° D、360°5. 某同学用5cm、7cm、9cm、13cm的四根小木棒摆出不同形状的三角形的个数为( )A、1 B、2 C、3 D、46. 如图给出的三角形有一部分被遮挡,则这个三角形可能是( )
A、45° B、50° C、40° D、60°4. 三角形的内角和是( )A、60° B、90° C、180° D、360°5. 某同学用5cm、7cm、9cm、13cm的四根小木棒摆出不同形状的三角形的个数为( )A、1 B、2 C、3 D、46. 如图给出的三角形有一部分被遮挡,则这个三角形可能是( ) A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形7. 已知两条线段a=12cm,b=5cm,下列线段能和a,b首尾顺次相接组成三角形的是( )A、18cm B、12cm C、7cm D、5cm8. 如图,为估计池塘岸边A、B两点的距离,小方在池塘的一侧选取一点O,OA=15米,OB=10米,A、B间的距离不可能是( )
A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形7. 已知两条线段a=12cm,b=5cm,下列线段能和a,b首尾顺次相接组成三角形的是( )A、18cm B、12cm C、7cm D、5cm8. 如图,为估计池塘岸边A、B两点的距离,小方在池塘的一侧选取一点O,OA=15米,OB=10米,A、B间的距离不可能是( ) A、5米 B、10米 C、15米 D、20米9. 在中,线段AP,AQ,AR分别是BC边上的高线,中线和角平分线,则( )A、 B、 C、 D、10. 三角形一边上的中线把原三角形分成两个( )A、形状相同的三角形
A、5米 B、10米 C、15米 D、20米9. 在中,线段AP,AQ,AR分别是BC边上的高线,中线和角平分线,则( )A、 B、 C、 D、10. 三角形一边上的中线把原三角形分成两个( )A、形状相同的三角形 B、面积相等的三角形
C、直角三角形
B、面积相等的三角形
C、直角三角形  D、周长相等的三角形
D、周长相等的三角形
二、填空题
-
11. 用海伦公式求面积的计算方法是: ,其中S表示三角形的面积,a,b,c分别表示三边之长,p表示周长的一半,即 .我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致,所以这个公式也叫“海伦-秦九韶式” .请你利用公式解答下列问题.在 中,已知三边之长 , , ,则 的面积为.12. 在△ABC中,若∠A=35°,∠B=65°,则∠C的度数为.13. 已知,在△ABC中,∠B=48°,∠C=68°,AD是BC边上的高,AE平分∠BAC,则∠DAE的度数为 .14. 如图,在△ABC中,∠A=70°,∠C=30°,点D为AC边上一点,过点D作DE∥AB,交BC于点E,且DE=BE,则∠BDE的度数是 .
 15. 已知的三个内角的度数之比:::: , 则 度, 度.16. 若三角形的底边为2m+1,高为2m,则此三角形的面积为.17. 三角形的两边长分别为4和6,那么第三边的取值范围是 .18. 如图,直线ED把分成一个和四边形BDEC,的周长一定大于四边形BDEC的周长,依据的原理是 .
15. 已知的三个内角的度数之比:::: , 则 度, 度.16. 若三角形的底边为2m+1,高为2m,则此三角形的面积为.17. 三角形的两边长分别为4和6,那么第三边的取值范围是 .18. 如图,直线ED把分成一个和四边形BDEC,的周长一定大于四边形BDEC的周长,依据的原理是 . 19. 已知三角形的两边长为3,5,则第三边的长度可以是(写出一个即可).20. 在△ABC中,∠B=60°,∠C=40°,AD、AE分别是△ABC的高线和角平分线,则∠DAE的度数为 .
19. 已知三角形的两边长为3,5,则第三边的长度可以是(写出一个即可).20. 在△ABC中,∠B=60°,∠C=40°,AD、AE分别是△ABC的高线和角平分线,则∠DAE的度数为 .三、解答题
-
21. 如图,在 中, 为 的高, 为 的角平分线, 交 于点G, , ,求 的大小.
 22. 如图,AD是的高,CE是的角平分线.若 , , 求的度数.
22. 如图,AD是的高,CE是的角平分线.若 , , 求的度数.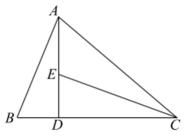 23. 已知:如图, , 点E在AC上.求证: .
23. 已知:如图, , 点E在AC上.求证: . 24. 先化简,再求值:
24. 先化简,再求值:, 其中a是已知两边分别为2和3的三角形的第三边长,且a是整数.
25. 如图所示,在△ABC中,点D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=66°,求∠DAC的度数.
四、综合题
-
26. 已知:如图,在Rt△ABC中,∠C=90°.
 (1)、做∠A的平分线交BC于点D(要求:尺规作图,保留作图痕迹,不写作法);(2)、若再作∠B的平分线交AD于点P,则∠APB的度数为°.27. 如图,在等腰中, , 为边上的高线,延长得射线 .
(1)、做∠A的平分线交BC于点D(要求:尺规作图,保留作图痕迹,不写作法);(2)、若再作∠B的平分线交AD于点P,则∠APB的度数为°.27. 如图,在等腰中, , 为边上的高线,延长得射线 . (1)、尺规作图,作的角平分线;(2)、求证: .28. 中,CD平分 , 点E是BC上一动点,连接AE交CD于点D.
(1)、尺规作图,作的角平分线;(2)、求证: .28. 中,CD平分 , 点E是BC上一动点,连接AE交CD于点D. (1)、如图1,若 , AE平分 , 则的度数为;(2)、如图2,若 , , , 则的度数为;(3)、如图3,在BC的右侧过点C作 , 交AE延长线于点F,且 , . 试判断AB与CF的位置关系,并证明你的结论.
(1)、如图1,若 , AE平分 , 则的度数为;(2)、如图2,若 , , , 则的度数为;(3)、如图3,在BC的右侧过点C作 , 交AE延长线于点F,且 , . 试判断AB与CF的位置关系,并证明你的结论.

