浙江省2022年中考数学真题分类汇编11 解直角三角形

试卷更新日期：2022-07-03 类型：二轮复习

进入出卷网下载

一、单选题

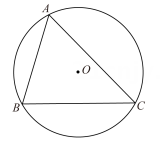
1. 如图，已知△ABC内接于半径为1的⊙O，∠BAC=θ（θ是锐角），则△ABC的面积的最大值为（）

A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)

查看试题解析
2. 一配电房示意图如图所示，它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为（）

A、 $(4 + 3 \sin α) m$ B、 $(4 + 3 \tan α) m$ C、 $(4 + \frac{3}{\sin α}) m$ D、 $(4 + \frac{3}{\tan α}) m$

查看试题解析
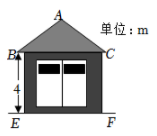3. 如图，已知菱形ABCD的边长为4，E是BC的中点，AF平分∠EAD交CD于点F，FG∥AD交AE于点G，若cosB＝ $\frac{1}{4}$ ，则FG的长是（）

A、3 B、 $\frac{8}{3}$ C、 $\frac{2 \sqrt{15}}{3}$ D、 $\frac{5}{2}$

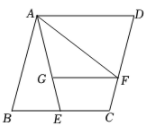查看试题解析

二、填空题

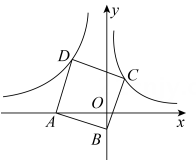
4. 如图，已知在平面直角坐标系xOy中，点A在x轴的负半轴上，点B在y轴的负半轴上，tan∠ABO=3，以AB为边向上作正方形ABCD．若图象经过点C的反比例函数的解析式是y= $\frac{1}{x}$ ，则图象经过点D的反比例函数的解析式是．

查看试题解析
5. 如图是某风车示意图，其相同的四个叶片均匀分布，水平地而上的点M在旋转中心O的正下方。某一时刻，太阳光线恰好垂直照射叶片 OA、OB ，此时各叶片影子在点M右侧成线段 CD ，测得MC=8.5m，CD=13m，垂直于地面的木棒 EF 与影子 FG 的比为2∶3，则点O，M之间的距离等于米．转动时，叶片外端离地面的最大高度等于米．

查看试题解析

三、解答题

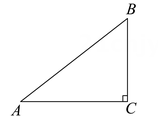
6. 如图，已知在Rt△ABC中，∠C=90°，AB=5，BC=3．求AC的长和sinA的值．

查看试题解析
7. 如图1，梯子斜靠在竖直的墙上，其示意图如图2，梯子与地面所成的角α为75° ，梯子AB长3m，求梯子顶部离地竖直高度BC．（结果精确到 0.1m；参考数据：sin75°≈0.97， cos75°≈0.26，tan75°≈3.73）

查看试题解析
8. 小华将一张纸对折后做成的纸飞机如图1，纸飞机机尾的横截面是一个轴对称图形，其示意图如图2，已知AD＝BE＝10cm，CD＝CE＝5cm，AD⊥CD，BE⊥CE，∠DCE＝40°．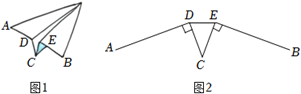

(1)、连结DE，求线段DE的长．

(2)、求点A，B之间的距离．
（结果精确到0.1cm．参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）

查看试题解析
9. 每年的11月9日是我国的“全国消防安全教育宣传日”，为了提升全民防灾减灾意识，某消防大队进行了消防演习．如图1，架在消防车上的云梯AB可伸缩（最长可伸至20m），且可绕点B转动，其底部B离地面的距离BC为2m，当云梯顶端A在建筑物EF所在直线上时，底部B到EF的距离BD为9m．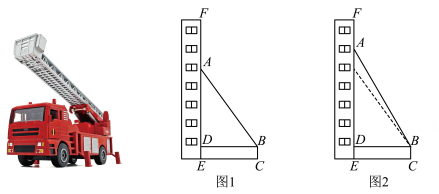

(参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3)

(1)、若∠ABD=53°，求此时云梯AB的长．

(2)、如图2，若在建筑物底部E的正上方19m处突发险情，请问在该消防车不移动位置的前提下，云梯能否伸到险情处？请说明理由．

查看试题解析
10. 如图，在Rt△ACB中，∠ACB=90°，点M为边AB的中点，点E在线段AM上，EF⊥AC于点F，连接CM，CE．已知∠A=50°，∠ACE=30°．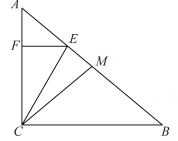

(1)、求证：CE=CM.

(2)、若AB=4，求线段FC的长.

查看试题解析
11. 如图，在△ABC 中， AD⊥BC于点D、E、F分别是AC、AB 的中点，O是 DF 的中点， EO 的延长线交线段 BD 于点G，连结 DE、EF、FG．

(1)、求证：四边形 DEFG 是平行四边形．

(2)、当AD=5，tan∠EDC= $\frac{5}{2}$ =时，求 FG 的长．

查看试题解析
12. 圭表（如图1）是我国古代一种通过测量正午日影长度来推定节气的天文仪器，它包括一根直立的标竿（称为“表”）和一把呈南北方向水平固定摆放的与标竿垂直的长尺（称为“圭”），当正午太阳照射在表上时，日影便会投影在圭面上，圭面上日影长度最长的那一天定为冬至，日影长度最短的那一天定为夏至.图2是一个根据某市地理位置设计的圭表平面示意图，表 AC垂直圭BC，已知该市冬至正午太阳高度角（即∠ABC）为37° ，夏至正午太阳高度角（即∠ADC）为84°，圭面上冬至线与夏至线之间的距离（即DB的长）为4米．

(1)、求∠BAD的度数．

(2)、求表AC的长（最后结果精确到0.1米）．
（参考数据：sin37°≈ $\frac{3}{5}$ ，cos37°≈ $\frac{4}{5}$ ，tan37°≈ $\frac{3}{4}$ ，tan84°≈ $\frac{19}{2}$ ）

查看试题解析
13. 在正方形ABCD中，点M是边AB的中点，点E在线段AM上（不与点A重合），点F在边BC上，且AE=2BF，连接EF，以EF为边在正方形ABCD内作正方形EFGH．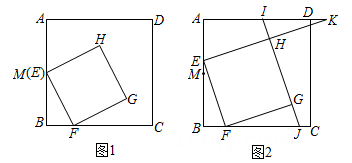

(1)、如图1．若AB=4，当点E与点M重合时，求正方形EFGH的面积

(2)、如图2．已知直线HG分别与边AD，BC交于点I，J，射线EH与射线AD交于点K．
①求证：EK=2EH；

②设∠AEK=α，△FGJ和四边形AEHI的面积分别为S₁、S₂ ．

求证： $\frac{S_{2}}{S_{1}}$ =4sin²α-1．

查看试题解析
14. 小东在做九上课本123页习题：“1： $\sqrt{2}$ 也是一个很有趣的比．已知线段AB（如图1），用直尺和圆规作AB上的一点P，使AP：AB＝1： $\sqrt{2}$ ．”小东的作法是：如图2，以AB为斜边作等腰直角三角形ABC，再以点A为圆心，AC长为半径作弧，交线段AB于点P，点P即为所求作的点．小东称点P为线段AB的“趣点”．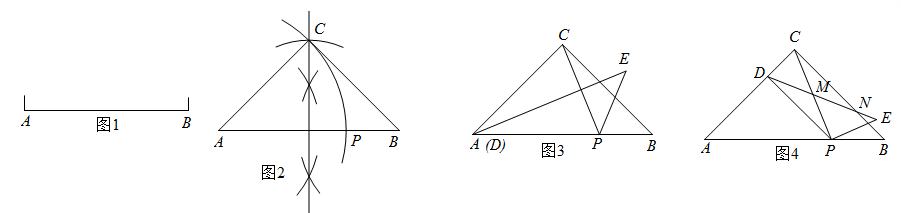

(1)、你赞同他的作法吗？请说明理由．

(2)、小东在此基础上进行了如下操作和探究：连结CP，点D为线段AC上的动点，点E在AB的上方，构造△DPE，使得△DPE∽△CPB．
①如图3，当点D运动到点A时，求∠CPE的度数．

②如图4，DE分别交CP，CB于点M，N，当点D为线段AC的“趣点”时（CD＜AD），猜想：点N是否为线段ME的“趣点”？并说明理由．

查看试题解析
15.

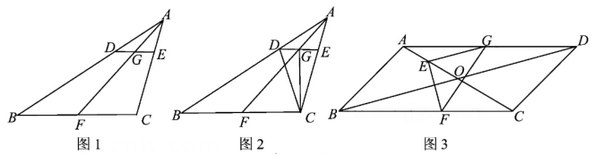(1)、【基础巩固】
如图1，在△ABC中，D，E，F分别为AB，AC，BC上的点，DE∥BC，BF=CF，AF交DE于点G，求证：DG= EG．

(2)、【尝试应用】
如图2，在(1)的条件下，连结CD，CG．若CG⊥DE，CD=6，AE=3，求 $\frac{D E}{B C}$ 的值．

(3)、【拓展提高】
如图3，在▱ABCD中，∠ADC=45°，AC与BD交于点O，E为AO上一点，EG∥BD交AD于点G，EF⊥EG交BC于点F．若∠EGF=40°，FG平分∠EFC，FG=10，求BF的长．

查看试题解析