浙江省2022年中考数学真题分类汇编10 图形的相似
试卷更新日期:2022-07-03 类型:二轮复习
一、单选题
-
1. 将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片 ,其中 , , , , ,则剪掉的两个直角三角形的斜边长不可能是( )
 A、 B、 C、10 D、2. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( )
A、 B、 C、10 D、2. 如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上:若线段AB=3,则线段BC的长是( ) A、 B、1 C、 D、23. 如图,在 中, ,以其三边为边向外作正方形,连结 ,作 于点M, 于点J, 于点K,交 于点L.若正方形 与正方形 的面积之比为5, ,则 的长为( )
A、 B、1 C、 D、23. 如图,在 中, ,以其三边为边向外作正方形,连结 ,作 于点M, 于点J, 于点K,交 于点L.若正方形 与正方形 的面积之比为5, ,则 的长为( )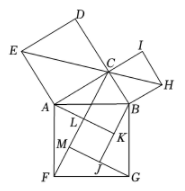 A、 B、 C、 D、4. 如图,在Rt△ABC和Rt△BDE中,∠ABC=∠BDE=90°,点A在边DE的中点上,若AB=BC,DB=DE=2,连结CE,则CE的长为( )
A、 B、 C、 D、4. 如图,在Rt△ABC和Rt△BDE中,∠ABC=∠BDE=90°,点A在边DE的中点上,若AB=BC,DB=DE=2,连结CE,则CE的长为( )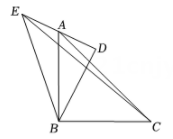 A、 B、 C、4 D、
A、 B、 C、4 D、二、填空题
-
5. 如图,已知在△ABC中,D,E分别是AB,AC上的点,DE∥BC, ,若DE=2,则BC的长是 .
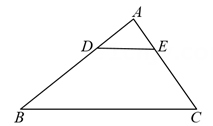 6. 某项目学习小组为了测量直立在水平地面上的旗杆AB的高度,把标杆DE直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72m,EF=2.18m.已知B,C,E,F在同一直线上,AB⊥BC,DE⊥EF,DE=2.47m,则AB=cm.
6. 某项目学习小组为了测量直立在水平地面上的旗杆AB的高度,把标杆DE直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72m,EF=2.18m.已知B,C,E,F在同一直线上,AB⊥BC,DE⊥EF,DE=2.47m,则AB=cm.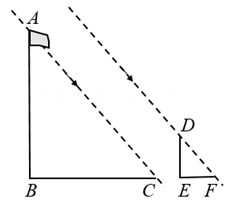
三、作图题
-
7. 如图,在6×6的方格纸中,点A,B,C均在格点上,试按要求画出相应格点图形,
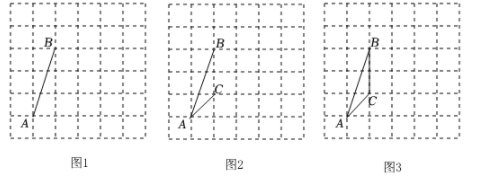 (1)、如图1,作一条线段,使它是AB向右平移一格后的图形;(2)、如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)、如图3,作一个与△ABC相似的三角形,相似比不等于1.
(1)、如图1,作一条线段,使它是AB向右平移一格后的图形;(2)、如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)、如图3,作一个与△ABC相似的三角形,相似比不等于1.四、解答题
-
8. 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,连接DE,EF.已知四边形BFED是平行四边形, 、
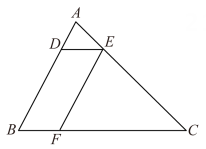 (1)、若AB=8,求线段AD的长.(2)、若△ADE的面积为1,求平行四边形BFED的面积.9. 如图,以AB为直径的⊙O与AH相切于点A,点C在AB左侧圆弧上,弦CD⊥AB交⊙O于点D,连结AC,AD,点A关于CD的对称点为E,直线CE交⊙O于点F,交AH于点G,
(1)、若AB=8,求线段AD的长.(2)、若△ADE的面积为1,求平行四边形BFED的面积.9. 如图,以AB为直径的⊙O与AH相切于点A,点C在AB左侧圆弧上,弦CD⊥AB交⊙O于点D,连结AC,AD,点A关于CD的对称点为E,直线CE交⊙O于点F,交AH于点G, (1)、求证:∠CAG=∠AGC:(2)、当点E在AB上,连结AF交CD于点卫,若 ,求 的值;(3)、当点E在射线AB上,AB=2,以点A,C,O,F为顶点的四边形中有一组对边平行时,求AE的长.10. 如图1,在正方形ABCD中,点F,H分别在边AD,AB上,连结AC,FH交于点E,已知CF=CH.
(1)、求证:∠CAG=∠AGC:(2)、当点E在AB上,连结AF交CD于点卫,若 ,求 的值;(3)、当点E在射线AB上,AB=2,以点A,C,O,F为顶点的四边形中有一组对边平行时,求AE的长.10. 如图1,在正方形ABCD中,点F,H分别在边AD,AB上,连结AC,FH交于点E,已知CF=CH. (1)、线段AC与FH垂直吗?请说明理由.(2)、如图2,过点A,H,F的圆交CF于点P,连结PH交AC于点K.求证:(3)、如图3,在(2)的条件下,当点K是线段AC的中点时,求 的值.11. 如图,在菱形ABCD中,AB=10. ,点E从点B出发沿折线B-C-D向终点D运动.过点E作点E所在的边(BC或CD)的垂线,交菱形其它的边于点F,在EF的右侧作矩形EFGH.
(1)、线段AC与FH垂直吗?请说明理由.(2)、如图2,过点A,H,F的圆交CF于点P,连结PH交AC于点K.求证:(3)、如图3,在(2)的条件下,当点K是线段AC的中点时,求 的值.11. 如图,在菱形ABCD中,AB=10. ,点E从点B出发沿折线B-C-D向终点D运动.过点E作点E所在的边(BC或CD)的垂线,交菱形其它的边于点F,在EF的右侧作矩形EFGH.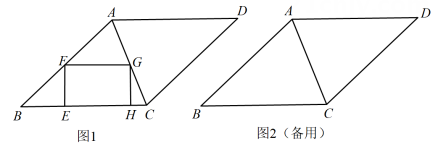 (1)、如图1,点G在AC上.求证:FA=FG.(2)、若EF=FG,当EF过AC中点时,求AG的长.(3)、已知FG=8,设点E的运动路程为s.当s满足什么条件时,以G,C,H为顶点的三角形与△BEF相似(包括全等)?12. 已知在Rt△ABC中,∠ACB=90°,a,b分别表示∠A,∠B的对边,a>b.记△ABC的面积为S.
(1)、如图1,点G在AC上.求证:FA=FG.(2)、若EF=FG,当EF过AC中点时,求AG的长.(3)、已知FG=8,设点E的运动路程为s.当s满足什么条件时,以G,C,H为顶点的三角形与△BEF相似(包括全等)?12. 已知在Rt△ABC中,∠ACB=90°,a,b分别表示∠A,∠B的对边,a>b.记△ABC的面积为S.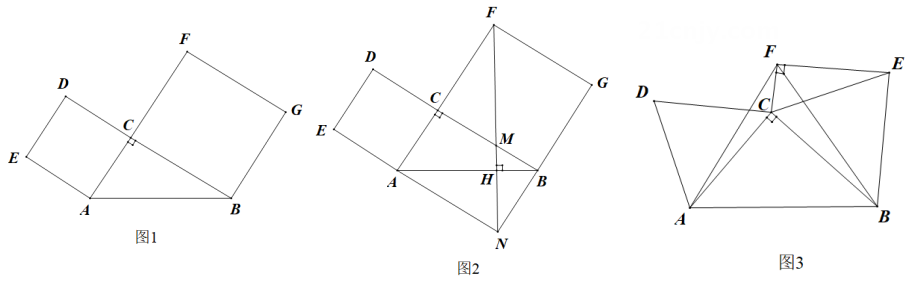 (1)、如图1,分别以AC,CB为边向形外作正方形ACDE和正方形BGFC.记正方形ACDE的面积为S1 , 正方形BGFC的面积为S2 .
(1)、如图1,分别以AC,CB为边向形外作正方形ACDE和正方形BGFC.记正方形ACDE的面积为S1 , 正方形BGFC的面积为S2 .①若S1=9,S2=16,求S的值;
②延长EA交GB的延长线于点N,连结FN,交BC于点M,交AB于点H.若FH⊥AB(如图2所示),求证:S2-S1=2S.
(2)、如图3,分别以AC,CB为边向形外作等边三角形ACD和等边三角形CBE,记等边三角形ACD的面积为S1 , 等边三角形CBE的面积为S2 . 以AB为边向上作等边三角形ABF(点C在△ABF内),连结EF,CF.若EF⊥CF,试探索S2-S1与S之间的等量关系,并说明理由.
-