浙江省2022年中考数学真题分类汇编09 图形的变换与视图
试卷更新日期:2022-07-03 类型:二轮复习
一、单选题
-
1. 如图是由四个相同的小立方体搭成的几何体,它的主视图是( )
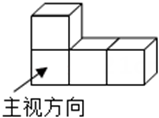 A、
A、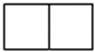 B、
B、 C、
C、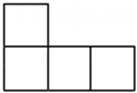 D、
D、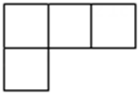
-
2. 如图是由四个相同的正方体搭成的立体图形,其主视图是( )
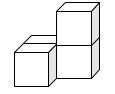 A、
A、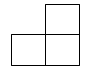 B、
B、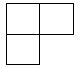 C、
C、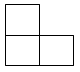 D、
D、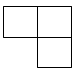
-
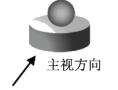
3. 如图所示几何体是由一个球体和一个圆柱组成的,它的俯视图是( )
 A、
A、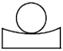 B、
B、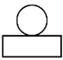 C、
C、 D、
D、
-
4. 如图是由四个相同的小正方体组成的几何体,它的主视图是( )
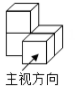 A、
A、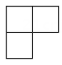 B、
B、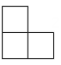 C、
C、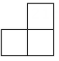 D、
D、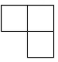
-
5. 某物体如图所示,它的主视图是( )
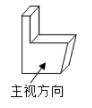 A、
A、 B、
B、 C、
C、 D、
D、
-
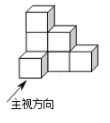
6. 由七个相同的小立方块搭成的几何体如图所示,则它的主视图是( )
 A、
A、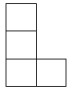 B、
B、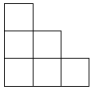 C、
C、 D、
D、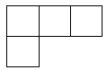
-
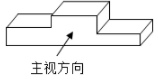
7. 如图是运动会领奖台,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
8. “方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
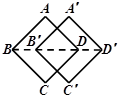 A、1cm B、2cm C、( -1)c. D、(2 -1)cm
A、1cm B、2cm C、( -1)c. D、(2 -1)cm -
9. 如图是战机在空中展示的轴对称队形.以飞机 B、C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(40,a),则飞机D的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是( )
 A、BD=10 B、HG=2 C、EG∥FH D、GF⊥BC
A、BD=10 B、HG=2 C、EG∥FH D、GF⊥BC -
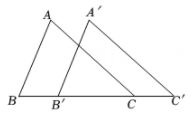
11. 如图,将△ABC沿BC方向平移1cm 得到对应的△A'B'C'.若B'C=2cm,则BC'的长是( )
 A、2cm B、3cm C、4cm D、5cm
A、2cm B、3cm C、4cm D、5cm -
12. 如图,在平面直角坐标系中,已知点P(0,2),点A(4,2).以点P为旋转中心,把点A按逆时针方向旋转60°,得点B.在M1( ,0),M2( ,-1),M3(1,4),M4(2, )四个点中,直线PB经过的点是( )
 A、M1 B、M2 C、M3 D、M4
A、M1 B、M2 C、M3 D、M4 -
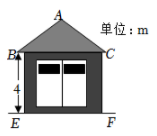
13. 一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14. 如图是一张矩形纸片ABCD,点E为AD中点,点F在BC上,把该纸片沿EF折叠,点A,B的对应点分别为A',B',A'E与BC相交于点G,B'A'的延长线过点C,若 ,则 的值为( )
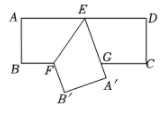 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
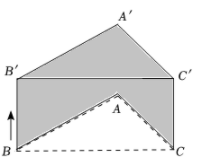
15. 如图, △ABC的边BC长为4cm.将△ABC平移2cm得到△A′B′C′ ,且BB′⊥BC,则阴影部分的面积为 .
-
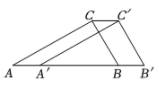
16. 如图,在Rt△ABC中, ∠ACB=90°,∠A=30°,BC=2cm .把 △ABC沿AB方向平移1cm,得到△A'B'C' ,连结CC',则四边形AB'C'C 的周长为cm..
-
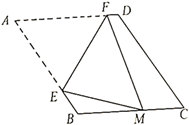
17. 如图,在菱形 ABCD中,∠A=60° ,AB=6.折叠该菱形,使点A落在边BC上的点M 处,折痕分别与边 AB,AD交于点E,F.当点M与点B重合时,EF的长为;当点M的位置变化时,DF长的最大值为 .
-
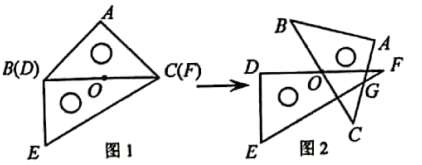
18. 一副三角板按图1放置,O是边BC(DF)的中点,BC=12cm.如图2,将△ABC绕点O顺时针旋转60°,AC与EF相交于点G,则FG的长是cm.
三、作图题
-
19. 如图,在 2×6 的方格纸中,已知格点P,请按要求画格点图形(顶点均在格点上).
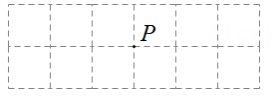
注:图1,图2在答题纸上.
(1)、在图1中画一个锐角三角形,使P为其中一边的中点,再画出该三角形向右平移2个单位后的图形.(2)、在图2中画一个以P为一个顶点的钝角三角形,使三边长都不相等,再画出该三角形绕点P旋转 180° 后的图形. -
20. 如图,在6×6的方格纸中,点A,B,C均在格点上,试按要求画出相应格点图形,
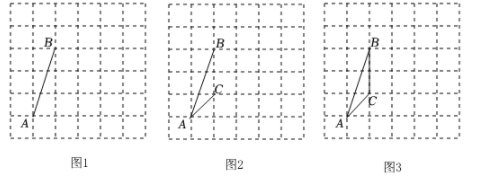 (1)、如图1,作一条线段,使它是AB向右平移一格后的图形;(2)、如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)、如图3,作一个与△ABC相似的三角形,相似比不等于1.
(1)、如图1,作一条线段,使它是AB向右平移一格后的图形;(2)、如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)、如图3,作一个与△ABC相似的三角形,相似比不等于1.
四、综合题
-
21. 如图,将矩形纸片ABCD折叠,使点B与点D重台,点A落在点P处,折痕为EF,
 (1)、求证:△PDE≌△CDF;(2)、若CD=4cm,EF=5cm,求BC的长.
(1)、求证:△PDE≌△CDF;(2)、若CD=4cm,EF=5cm,求BC的长. -
22. 根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材1
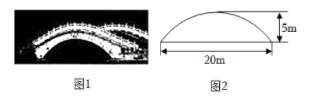
图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽 20m ,拱顶离水面 5m .据调查,该河段水位在此基础上再涨 1.8m 达到最高.
素材2
为迎佳节,拟在图1桥洞前面的桥拱上悬挂 40cm 长的灯笼,如图3.为了安全,灯笼底部距离水面不小于 1m ;为了实效,相邻两盏灯笼悬挂点的水平间距均为 1.6m ;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
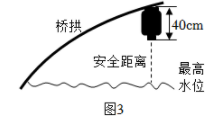
问题解决
任务1
确定桥拱形状
在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2
探究悬挂范围
在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
任务3
拟定设计方案
给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
