浙江省2022年中考数学真题分类汇编08 圆

试卷更新日期：2022-07-03 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图，在⊙O中，∠BOC＝130°，点A在 $\overset{⌢}{B A C}$ 上，则∠BAC的度数为（）

A、55° B、65° C、75° D、130°

查看试题解析
2. 已知圆锥的底面半径为4cm，母线长为6cm，则圆锥的侧面积为（）

A、36πcm² B、24πcm² C、16πcm² D、12πcm²

查看试题解析
3. 如图， AB、AC是 ⊙O 的两条弦， OD⊥AB于点D， OE⊥AC 于点E，连结 OB、OC．若 ∠DOE=130° ，则 ∠BOC 的度数为（）

A、95° B、100° C、105° D、130°

查看试题解析
4. 某仿古墙上原有一个矩形的门洞，现要将它改为一个圆弧形的门洞，圆弧所在的圆外接于矩形，如图.已知矩形的宽为2m，高为2 $\sqrt{3}$ m，则改建后门洞的圆弧长是（）

A、 $\frac{5 π}{3}$ m B、 $\frac{8 π}{3}$ m C、 $\frac{10 π}{3}$ m D、（ $\frac{5 π}{3}$ +2）m

查看试题解析

二、填空题

5. 如图，在△ABC中，AC=2，BC=4，点O在BC上，以OB为半径的圆与AC相切于点A．D是BC边上的动点，当△ACD为直角三角形时，AD的长为

查看试题解析
6. 如图，已知AB是⊙O的弦，∠AOB=120°，OC⊥AB，垂足为C，OC的延长线交⊙O于点D．若∠APD是 $\overset{⌢}{A D}$ 所对的圆周角，则∠APD的度数是

查看试题解析
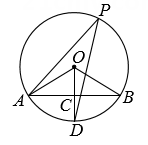7. 如图是以点O为圆心，AB为直径的圆形纸片．点C在⊙O上，将该圆形纸片沿直线CO对折，点B落在⊙O上的点D处（不与点A重合），连接CB，CD，AD．设CD与直径AB交于点E．若AD=ED，则∠B=度； $\frac{B C}{A D}$ 的值等于．

查看试题解析
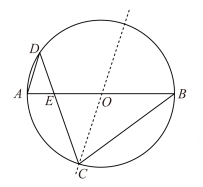8. 若扇形的圆心角为 120° ，半径为 $\frac{3}{2}$ ，则它的弧长为．

查看试题解析
9. 如图，木工用角尺的短边紧靠⊙О于点A，长边与⊙О相切于点B，角尺的直角顶点为C，已知AC=6cm，CB=8cm，则⊙О的半径为cm.

查看试题解析
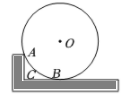10. 如图，在扇形AOB中，点C，D在 $\overset{⌢}{A B}$ 上，将 $\overset{⌢}{C D}$ 沿弦CD折叠后恰好与OA，OB相切于点E，F. 已知∠AOB＝120°，OA＝6，则 $\overset{⌢}{E F}$ 的度数为，折痕CD的长为．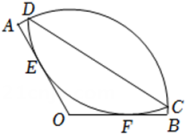

查看试题解析

三、解答题

11. 如图，在 △ABC中，AB=AC ，以AB为直径的⊙O与BC交于点D，连接AD．

(1)、求证： BD=CD；

(2)、若⊙O 与AC 相切，求∠B的度数；

(3)、用无刻度的直尺和圆规作出劣弧 $\overset{⌢}{A D}$ 的中点 E．（不写作法，保留作图痕迹）

查看试题解析
12. 如图，已知在Rt△ABC中，∠C=90°，D是AB边上一点，以BD为直径的半圆O与边AC相切，切点为E，过点O作OF⊥BC，垂足为F．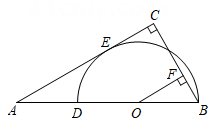

(1)、求证：OF=EC；

(2)、若∠A=30°，BD=2，求AD的长．

查看试题解析
13. 如图，半径为6的⊙O与Rt△ABC的边AB相切于点A，交边BC于点C，D，∠B=90°，连结OD，AD．

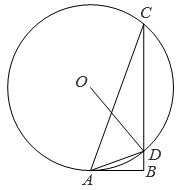(1)、若∠ACB=20°，求 $\overset{⌢}{A D}$ 的长（结果保留π）．

(2)、求证：AD平分∠BDO．

查看试题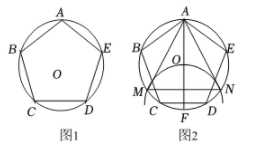解析
14. 如图

如图1，正五边形ABCDE内接于⊙O，阅读以下作图过程，并回答下列问题：

作法如图2.

1.作直径AF.

2.以F为圆心，FO为半径作圆弧，与⊙O交于点M，N.

3.连结AM，MN，NA.

(1)、求∠ABC的度数.

(2)、△AMN是正三角形吗？请说明理由.

(3)、从点A开始，以DN长为半径，在⊙O上依次截取点，再依次连结这些分点，得到正n边形，求n的值.

查看试题解析
15. 如图1，⊙O为锐角三角形ABC的外接圆，点D在BC上，AD交BC于点E，点F在AE上，满足∠AFB-∠BFD=∠ACB，FG∥AC交BC于点G，BE=FG，连结BD，DG．设∠ACB=α．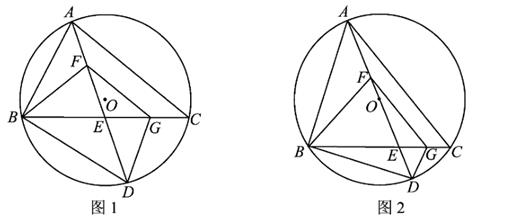

(1)、用含α的代数式表示∠BFD．

(2)、求证：△BDE≌△FDG．

(3)、如图2，AD为⊙O的直径．
①当 $\overset{⌢}{A B}$ 的长为2时，求 $\overset{⌢}{A C}$ 的长．

②当OF：OE=4：11时，求cosα的值．

查看试题解析
16. 如图1， AB 为半圆O的直径，C为 BA 延长线上一点， CD 切半圆于点D， BE⊥CD ，交 CD 延长线于点E，交半圆于点F，已知BC=5，BE=3．点P，Q分别在线段 AB、BE上（不与端点重合），且满足 $\frac{A P}{B Q} = \frac{5}{4}$ ．设BQ=x，CP=y．

(1)、求半圆O的半径．

(2)、求y关于x的函数表达式．

(3)、如图2，过点P作 PR⊥CE 于点R，连结 PQ、RQ．
①当 △PQR 为直角三角形时，求x的值．

②作点F关于 QR 的对称点 F' ，当点 F'落在 BC上时，求 $\frac{C F^{'}}{B F^{'}}$ 的值．

查看试题解析
17. 如图1，在正方形ABCD中，点F，H分别在边AD，AB上，连结AC，FH交于点E，已知CF=CH．

(1)、线段AC与FH垂直吗？请说明理由．

(2)、如图2，过点A，H，F的圆交CF于点P，连结PH交AC于点K．求证： $\frac{K H}{C H} = \frac{A K}{A C}$

(3)、如图3，在(2)的条件下，当点K是线段AC的中点时，求 $\frac{C P}{P F}$ 的值．

查看试题解析
18. 如图，以AB为直径的⊙O与AH相切于点A，点C在AB左侧圆弧上，弦CD⊥AB交⊙O于点D，连结AC，AD，点A关于CD的对称点为E，直线CE交⊙O于点F，交AH于点G，

(1)、求证：∠CAG=∠AGC：

(2)、当点E在AB上，连结AF交CD于点卫，若 $\frac{EF}{CE} = \frac{2}{5}$ ，求 $\frac{DP}{CP}$ 的值；

(3)、当点E在射线AB上，AB=2，以点A，C，O，F为顶点的四边形中有一组对边平行时，求AE的长.

查看试题解析