浙江省2022年中考数学真题分类汇编06 图形基础与三角形
试卷更新日期：2022-07-03 类型：二轮复习
一、单选题
-
1. 如图，已知∠1=90° ，为保证两条铁轨平行，添加的下列条件中，正确的是（ ）
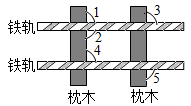A、 B、 C、 D、2. 如图，CD⊥AB于点D，已知∠ABC是钝角，则（ ）
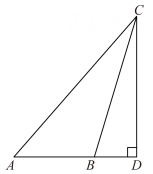A、线段CD是△ABC的AC边上的高线 B、线段CD是△ABC的AB边上的高线 C、线段AD是△ABC的BC边上的高线 D、线段AD是△ABC的AC边上的高线3. 如图，圆柱的底面直径为AB，高为AC.一只蚂蚁在C处，沿圆柱的侧面爬到B处，现将圆柱侧面沿AC“剪开”，在侧面展开图上画出蚂蚁爬行的最近路线，正确的是（ ）
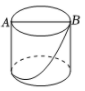A、
B、
C、
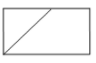D、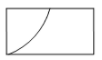
4. 如图，AC与BD相交于点O，OA=OD，OB=OC，不添加辅助线，判定△ABO≌△DCO的依据是（ ）
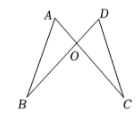A、SSS B、SAS C、AAS D、HL5. 如图，已知AB∥CD，点E在线段AD上(不与点A，点D重合)，连接CE．若∠C=20°，∠AEC=50°，则∠A=（ ）
A、10° B、20° C、30° D、40°6. 如图，点 D在 △ABC的边BC上，点 P在射线 AD上（不与点 A，D重合），连接PB， PC．下列命题中，假命题是（ ）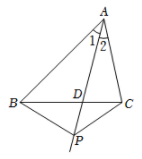
A、若 ， ，则 B、若 ， ，则 C、若 ， ，则 D、若 ， ，则7. 在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．如图，在6×6的正方形网格图形ABCD中，M，N分别是AB，BC上的格点，BM=4，BN=2．若点P是这个网格图形中的格点，连结PM，PN，则所有满足∠MPN=45°的△PMN中，边PM的长的最大值是（ ）
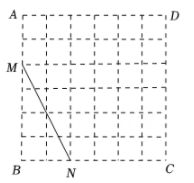A、 B、6 C、 D、8. 如图，把一块三角板 ABC 的直角顶点B放在直线 EF 上， ∠C=30° ，AC∥EF，则 ∠1= （ ）
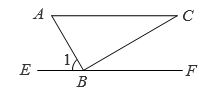A、30° B、45° C、60° D、75°9. 用尺规作一个角的角平分线，下列作法中错误的是（ ）A、
B、
C、
D、
二、填空题
-
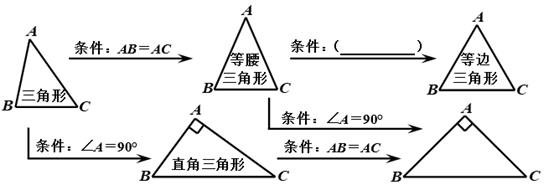
10. 正八边形一个内角的度数是.11. 小曹同学复习时将几种三角形的关系整理如图，请帮他在括号内填上一个适当的条件 ．
12. 如图，在△ABC中，∠ABC＝90°，∠A＝60°，直尺的一边与BC重合，另一边分别交AB，AC于点D，E．点B，C，D，E处的读数分别为15，12，0，1，则直尺宽BD的长为 ．
13. 如图，在△ABC 中， ∠ABC=40°， ∠BAC=80°，以点 A为圆心， AC 长为半径作弧，交射线 BA 于点 D，连结 CD ，则 ∠BCD 的度数是 ．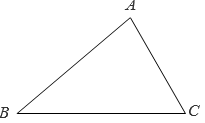
14. 如图，在Rt△ABC中， ∠ACB=90°，∠A=30°，BC=2cm .把 △ABC沿AB方向平移1cm，得到△A'B'C' ，连结CC'，则四边形AB'C'C 的周长为cm..
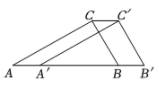15. 一副三角板按图1放置，O是边BC（DF）的中点，BC=12cm.如图2，将△ABC绕点O顺时针旋转60°，AC与EF相交于点G，则FG的长是cm．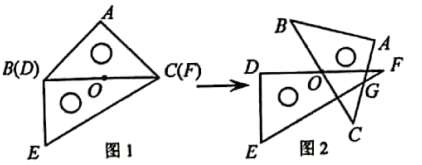
三、解答题
-
16. 如图，在Rt△ACB中，∠ACB=90°，点M为边AB的中点，点E在线段AM上，EF⊥AC于点F，连接CM，CE．已知∠A=50°，∠ACE=30°．
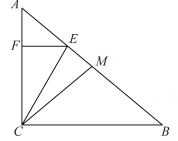(1)、求证：CE=CM.(2)、若AB=4，求线段FC的长.17. 如图， BD 是 △ABC的角平分线， DE∥BC ，交 AB 于点E．
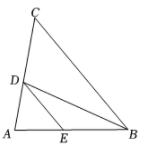(1)、求证： ．(2)、当AB=AC时，请判断 CD 与ED的大小关系，并说明理由．
